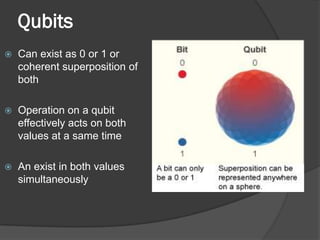
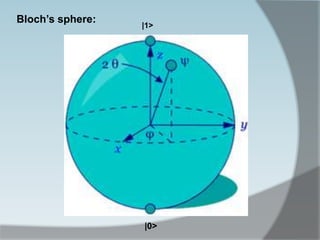
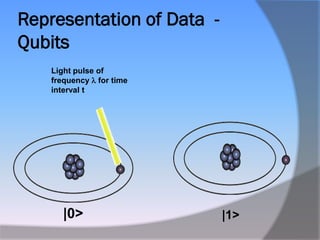
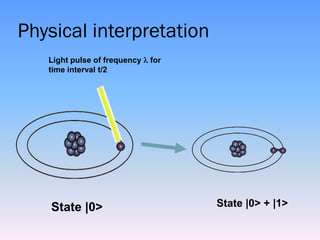
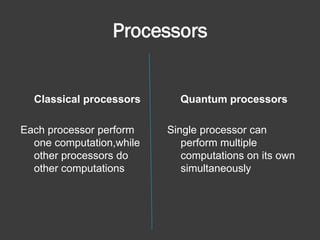
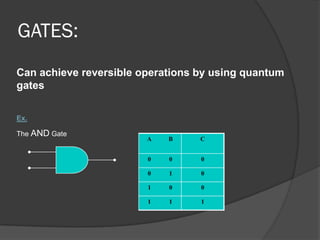
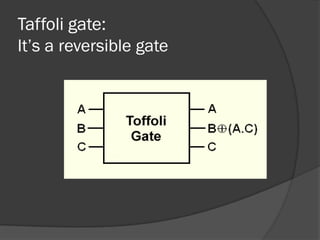
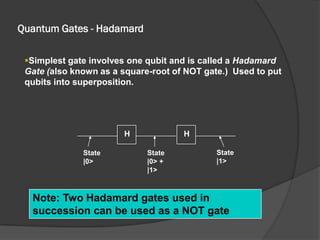
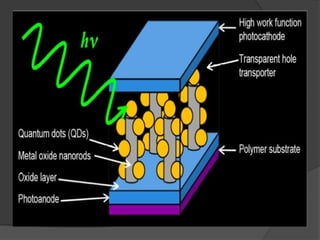
The document discusses quantum computing, emphasizing its reliance on qubits, which can exist in multiple states simultaneously, unlike classical bits. It highlights the advantages of quantum computers, such as significantly faster processing times for complex calculations, exemplified by Shor's algorithm for factoring large numbers. Additionally, it addresses the necessity for novel technologies, such as nanotechnology, to create these advanced computational systems.

1. Quantum computation
Based on nanotechnology
By:
M.Revanth kumar
T.Sri kanth

2. Speed of computation:
 Vaccum tubes
 Transistors
 Devices that perform
quantum computing

3. Quantum mechanics
Physical phenomena at
microscopic scales
Completely different from
classical mechanics

4. Quantum computing
 Theoretical study of
quantum systems
 Those systems are
applied to make a
quantum computer
 Uses “QUBITS”

5. Bits (classical computing)
 A bit can exist only in one
state
Either 0 or 1
 Information behaviour : one
single direction
 Logic gates are irreversible

6. Qubits
 Can exist as 0 or 1 or
coherent superposition of
both
 Operation on a qubit
effectively acts on both
values at a same time
 An exist in both values
simultaneously

7. Bloch’s sphere:
|1>
|0>

8. Ket notation:
q= a l0> + b l1>
Qubit system No. of
(n) operations
2 4
3 8
4 16

9. Representation of Data -
Qubits
Light pulse of
frequency  for time
interval t
|0> |1>

10. Physical interpretation
Light pulse of frequency  for
time interval t/2
State |0> State |0> + |1>

11. Representation of Data -
Superposition
 A single qubit can be forced into a superposition
of the two states denoted by the addition of the
state vectors:
|> =  |0> +  |1>
 Where  and  are complex numbers and | |
+ | | =1

12. Processors
Classical processors Quantum processors
Each processor perform Single processor can
one computation,while perform multiple
other processors do computations on its own
other computations simultaneously

13. As increase in no.of Qubits
 Increase in quantum parallelism
Solve
Quantum parallelism problems in
+ fraction of
Algorithm time

14. GATES:
Can achieve reversible operations by using quantum
gates
Ex.
The AND Gate
A B C
0 0 0
0 1 0
1 0 0
1 1 1

15. Reversible operations
 For a computer to run fast
 Inputs can be correctly deduced from
outputs
 Irreversible computation involve loss of
information

16. Taffoli gate:
It’s a reversible gate

17. Quantum Gates - Hadamard
Simplest gate involves one qubit and is called a Hadamard
Gate (also known as a square-root of NOT gate.) Used to put
qubits into superposition.
H H
State State State
|0> |0> + |1>
|1>
Note: Two Hadamard gates used in
succession can be used as a NOT gate

18. Quantum computer
 Use direct use of quantum mechanical
phenomena
 Utilizes quantum properties to represent data
 Could solve certain problems much faster

19. Shor’s algorithm
 Allows extremely quick factoring
 To factor a 1000 digit number
 For a classical computer it take 10
million billion years
 For a quantum computer its just 20 min

20. Building a quantum computer
 It can’t be from transistor and diodes
 A new type of technology is needed
 A technology that enables qubits to exist
as coherent superposition of 0 and 1

21. Why Nanotechnology is applied?

23. References
 Text books: 1. Palanisamy
2. A quantum revolution for computing. Julian
Brown, New Scientist 24/9/94
 Wikipedia.org
 Videos on quantum computation by
“centre for quantum computation and
communication technology”

24. Queries
?

25. What ever may be the technology we
come up with, should able to reach a
common man.