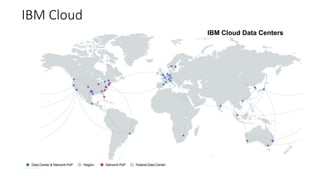
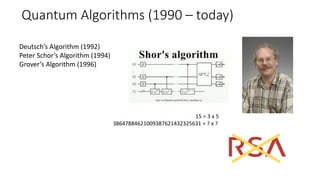
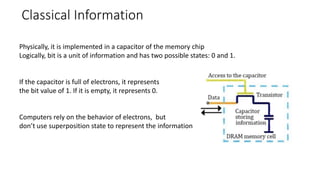
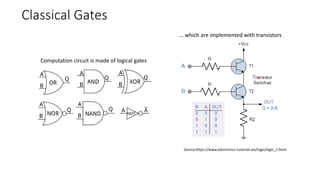
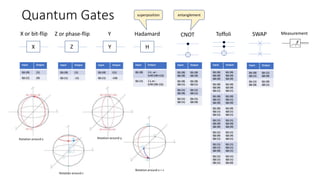
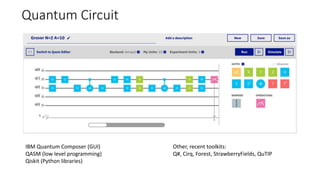
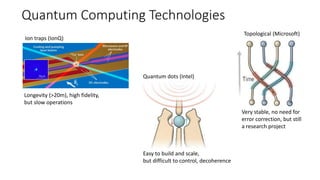
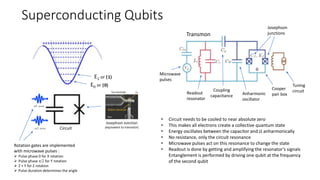
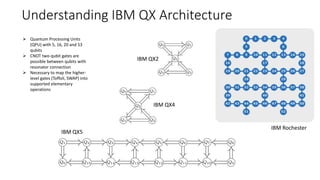
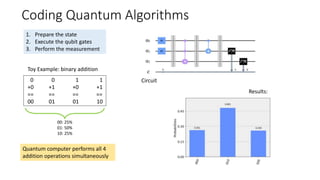
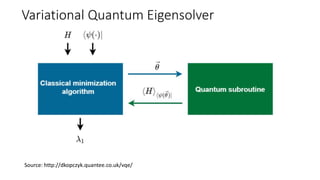
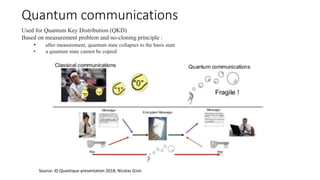
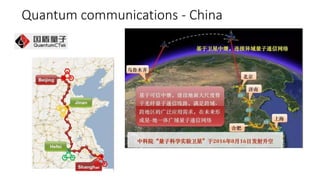
The document discusses the significance of quantum computing technologies, their problems and achievements, and the future landscape of the field. It covers the evolution of quantum algorithms, the advancements made by IBM and other entities in quantum computing, and various quantum computing technologies and applications. Additionally, it outlines the challenges of developing large-scale quantum computers and the implications of quantum communications.