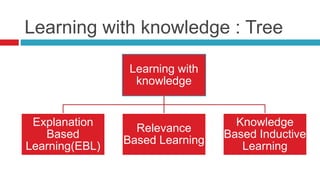
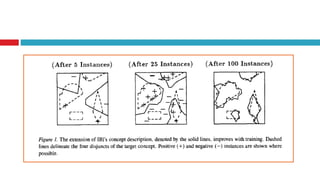
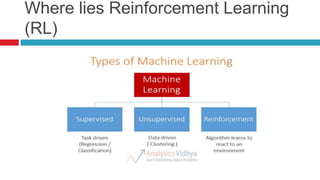
The document discusses various learning models in artificial intelligence, focusing on learning agents which consist of components like learning elements, performance elements, critics, and problem generators. It outlines different types of learning, including inductive learning, reinforcement learning, and the utilization of prior knowledge through methods like explanation-based learning and relevance-based learning. Additionally, it highlights the differences between neural networks and belief networks in terms of structure, representation, and learning processes.

1. LEARNING IN AI
Prof.Mrs.Minakshi P.Atre, PVGCOET,
SPPU

2. Basic Learning Model
 Learning agent’s components
 learning element -- the part of the agent responsible for
improving its performance
 performance element -- the part that chooses the actions
to take
 critic -- tells the learning element how the agent is doing
 problem generator -- suggests actions that could lead to
new, informative experiences (suboptimal from the point of
view of the performance element, but designed to improve
that element)

3. Issues in designing learning
system
 components -- which parts of the
performance element are to be improved
 representation of those components
 feedback available to the system
 prior information available to the system

4. All learning can be thought of as
learning the representation of a
function.

5. Types of
Learning
Speed up
learning
Learning
by taking
advice
Learning
from
example
Clustering
Learning
by
analogy
discovery

6. 1. Speed up learning
 A type of deductive learning that requires no
additional input, but improves the agent's
performance over time. There are two kinds,
rote learning and generalization (e.g., EBL).
Data caching is an example of how it would be
used.

7. 2. Learning by taking advice
 Deductive learning in which the system can
reason about new information added to its
knowledge base.
 McCarthy proposed the "advice taker" which
was such a system, and TEIRESIAS [Davis,
1976] was the first such system.

8. 3. Learning from example
 Inductive learning in which concepts are
learned from sets of labeled instances.

9. 4. Clustering
 Unsupervised, inductive learning in which
"natural classes" are found for data instances,
as well as ways of classifying them.
 Examples include COBWEB, AUTOCLASS.

10. 5. Learning by Analogy
 Inductive learning in which a system transfers
knowledge from one database into a that of a
different domain.

11. 6. Discovery
 Both inductive and deductive learning in which
an agent learns without help from a teacher.
 It is deductive if it proves theorems and
discovers concepts about those theorems;
 it is inductive when it raises conjectures.

12. What is Inductive Learning?
 Inductive learning is a kind of learning in which, given a
set of examples an agent tries to estimate or create an
evaluation function.
 Most inductive learning is supervised learning, in which
examples provided with classifications. (The alternative
is clustering.)
 More formally, an example is a pair (x, f(x)), where x is
the input and f(x) is the output of the function applied to
x.
 The task of pure inductive inference (or induction) is,

13. Bayesian Learning in Belief
Networks
 Bayesian learning maintains a number of
hypotheses about the data, each one weighted
its posterior probability when a prediction is
made
 The idea is that, rather than keeping only one
hypothesis, many are entertained, and
weighted based on their likelihoods.

14.  maintaining and reasoning with a large number of
hypotheses can be intractable
 most common approximation is to use a most
probable hypothesis, that is, an Hi of H that
maximizes P(Hi | D), where D is the data
 This is often called the maximum a posteriori
(MAP) hypothesis HMAP:
 P(X | D) ~= P(X | HMAP) x P(HMAP | D)

15. To find HMAP, we apply Bayes' rule:
 P(Hi | D) = [P(D | Hi) x P(Hi)] / P(D)
 Since P(D) is fixed across the hypotheses, we
only need to maximize the numerator
 The first term represents the probability that this
particular data set would be seen, given Hi as the
model of the world
 The second is the prior probability assigned to the
model.

16. Belief Network Learning
Problems
 Four kinds of belief networks
 depending upon whether the structure of the
network is known or unknown,
 and whether the variables in the network are
observable or hidden

17. Belief Networks
1. known structure, fully observable -- In this case
the only learnable part is the conditional probability
tables. These can be estimated directly using the
statistics of the sample data set.
2. unknown structure, fully observable -- Here the
problem is to reconstruct the network topology. The
problem can be thought of as a search through
structure space, and fitting data to each structure
reduces to the fixed-structure problem, so the MAP
or ML probability value can be used as a heuristic in
hill-climbing or SA search.

18. 3. known structure, hidden variables -- This is
analagous to neural network learning.
4. unknown structure, hidden variables -- When
some variables are unobservable, it becomes
difficult to apply prior techniques for recovering
structure, but they require averaging over all
possible values of the unknown variables.
No good general algorithms are known for
handling this case

19. Comparison between NN and Belief
Networks
 Similarities
 Both kinds of network are attribute-based
representations
 Both can handle either discrete or continuous
output

20. Differences between NN and Belief
N/w

21. NN Belief N/W
 neural networks are
distributed
 nodes generally don't
represent specific
propositions, and the
calculations would not
treat them in a
semantically-
meaningful way
 belief networks are
localized
representations
 Belief network nodes
represent
propositions with
clearly defined
semantics and
relationships to other
nodes

22. NN Belief N/W
 effect is that human
beings can neither
construct nor
understand neural
network
representations
 both can be done
with belief networks

23. NN Belief N/W
 Neural network
outputs could be
values or
probabilities, but they
cannot handle both
simultaneously
 Belief networks
handle two kinds of
activation, both in
terms of the values
a proposition may
take, and the
probabilities
assigned to each

24. NN Belief N/W
 Trained feed-forward
neural network
inference can execute
in linear time
 a neural network may
have to be
exponentially larger to
represent the same
things that a belief
network can.
 where in belief
networks inference
is NP-hard

25. As for learning, belief networks have
the advantages
 being easier to give prior knowledge;
 also, since they represent propositions locally,
it may be easier for them to converge,
 since they are directly affected only by a small
number of other propositions.

26. Reinforcement Learning

27. What is the reinforcement
learning
 As opposed to supervised learning,
reinforcement learning takes place in an
environment where the agent cannot directly
compare the results of its action to a desired
result

28. Reinforcement learning
 it is given some reward or punishment that
relates to its actions
 It may win or lose a game, or be told it has
made a good move or a poor one
 job of reinforcement learning is to find a
successful function using these rewards

29. Where lies Reinforcement Learning
(RL)

30. Block Schematic and example of
RL

31. Supervised vs
Reinforcement Learning
 Supervised learning: has external supervisor
 supervisor has knowledge of the environment
and shares it with the agent to complete the
task
 there are some problems in which there are so
many combinations of subtasks that the agent
can perform to achieve the objective
 creating a “supervisor” is almost impractical

32. Example
 in a chess game, there are tens of thousands of moves that
can be played
 creating a knowledge base that can be played is a tedious
task
 In these problems, it is more feasible to learn from one’s own
experiences and gain knowledge from them
 This is the main difference that can be said of reinforcement
learning and supervised learning.
 In both supervised and reinforcement learning, there is a
mapping between input and output.
 But in reinforcement learning, there is a reward function
which acts as a feedback to the agent as opposed to

33. Unsupervised vs Reinforcement
Learning:
 In reinforcement learning, there’s a mapping
from input to output--not present in
unsupervised learning
 unsupervised learning, the main task is to find
the underlying patterns rather than the
mapping

34. Example
 if the task is to suggest a news article to a user,
an unsupervised learning algorithm will look at
similar articles which the person has previously
read and suggest anyone from them.
 Whereas a reinforcement learning algorithm will
get constant feedback from the user by
suggesting few news articles and then build a
“knowledge graph” of which articles will the
person like

35. Summarizing Reinforcement
Learning
 The reason reinforcement learning is harder
than supervised learning is that the agent is
never told what the right action is, only
whether it is doing well or poorly, and in some
cases (such as chess) it may only receive
feedback after a long string of actions

36. Two basic kinds of information an
agent can try to learn in RL
 utility function -- The agent learns the utility of
being in various states, and chooses actions to
maximize the expected utility of their outcomes.
This requires the agent keep a model of the
environment
 action-value -- The agent learns an action-value
function giving the expected utility of performing
an action in a given state. This is called Q-
learning. This is the model-free approach.

37. Passive Learning in a known
environment
 Def:
 Assuming an environment consisting of a set
of states, some terminal and some non-
terminal, and a model that specifies the
probabilities of transition from state to state, an
agent learns passively by observing a set of
training sequences, which consist of a set of
state transitions followed by a reward

38.  The goal is to use the reward information to
learn the expected utility of each of the non-
terminal states.
 An important simplifying assumption is
that the utility of a sequence is the sum of
the rewards accumulated in the states of
the sequence.
 That is, the utility function is additive

39.  A passive learning agent keeps an estimate U
of the utility of each state, a table N of how
many times each state was seen, and a table
M of transition probabilities.
 There are a variety of ways the agent can
update its table U

40. Two types of passive learning in
known environment
Passive
Learning
Naïve
Updating
Adaptive
Dynamic
Programming
Temporal
Difference
Learning

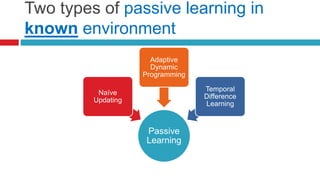
41. 1. Naive Updating
 One simple updating method is the least mean
squares (LMS) approach [Widrow and Hoff,
1960].
 It assumes that the observed reward-to-go of a
state in a sequence provides direct evidence
of the actual reward-to-go.
 The approach is simply to keep the utility as a
running average of the rewards based upon
the number of times the state has been seen

42.  This approach minimizes the mean square
error with respect to the observed data
 This approach converges very slowly, because
it ignores the fact that the actual utility of a
state is the probability-weighted average of
its successors' utilities, plus its own
reward. LMS disregards these probabilities.

43. 2.Adaptive Dynamic Programming
 If the transition probabilities and the rewards of
the states are known (which will usually
happen after a reasonably small set of training
examples), then the actual utilities can be
computed directly as
 U(i) = R(i) + SUMj MijU(j)
where U(i) is the utility of state i, R is its reward,
and Mij is the probability of transition from state i

44.  This is identical to a single value determination in
the policy iteration algorithm for Markov decision
processes.
 Adaptive dynamic programming is any kind of
reinforcement learning method that works by
solving the utility equations using a dynamic
programming algorithm.
 It is exact, but of course highly inefficient in large
state spaces

45. 3. Temporal Difference Learning
 uses the difference in utility values between
successive states to adjust them from one epoch
to another
 key idea is to use the observed transitions to
adjust the values of the observed states so that
they agree with the ADP constraint equations
 Practically, this means updating the utility of state i
so that it agrees better with its successor j.

46.  This is done with the temporal-difference (TD)
equation:
 U(i) <- U(i) + a(R(i) + U(j) - U(i))
 where a is a learning rate parameter
Temporal difference learning is a way of
approximating the ADP constraint equations
without solving them for all possible states

47.  The idea generally is to define conditions that hold
over local transitions when the utility estimates are
correct, and then create update rules that nudge the
estimates toward this equation.
 This approach will cause U(i) to converge to the
correct value if the learning rate parameter decreases
with the number of times a state has been visited
[Dayan, 1992].
 In general, as the number of training sequences tends
to infinity, TD will converge on the same utilities as
ADP.

48. Passive Learning in an Unknown
Environment
 neither temporal difference learning nor LMS
actually use the model M of state transition
probabilities
 they will operate unchanged in an unknown
environment
 The ADP approach, however, updates its
estimated model of an unknown environment
after each step, and this model is used to
revise the utility estimates

49.  Any method for learning stochastic functions
can be used to learn the environment model;
 in particular, in a simple environment the
transition probability Mij is just the percentage
of times state i has transitioned to j

50. Basic difference between TD and
ADP:
 TD adjusts a state to agree with the observed
successor, while ADP makes a state agree with all
successors that might occur, weighted by their
probabilities
 ADP's adjustments may need to be propagated
across all of the utility equations, while TD's affect
only the current equation.
 TD is essentially a crude first approximation to

51.  A middle-ground can be found by bounding or
ordering the number of adjustments made in ADP,
beyond the simple one made in TD
 The prioritized-sweeping heuristic prefers only to
make adjustments to states whose likely
successors have just undergone large
adjustments in their utility estimates
 Such approximate ADP systems can be very
nearly as efficient as ADP in terms of
convergence, but operate much more quickly

52. Active Learning in an Unknown
Environment
 difference between active and passive agents is
that passive agents learn a fixed policy, while
the active agent must decide what action to
take and how it will affect its rewards
 To represent an active agent, the environment
model M is extended to give the probability of a
transition from a state i to a state j, given an action
a

53.  Utility is modified to be the reward of the state
plus the maximum utility expected depending
upon the agent's action:
 U(i) = R(i) + maxa x SUMj Ma
ijU(j)
 An ADP agent is extended to learn transition
probabilities given actions; this is simply another
dimension in its transition table
 A TD agent must similarly be extended to have a
model of the environment.

54. Learning with Knowledge

55. Learning with knowledge : Tree
Learning with
knowledge
Explanation
Based
Learning(EBL)
Relevance
Based Learning
Knowledge
Based Inductive
Learning

56. Learning with knowledge
 considering the kinds of logical constraints
placed upon different kinds of knowledge-
based learning, we can classify them more
clearly
 Examples are composed of Descriptions and
Classifications, and we are trying to find a
Hypothesis to explain the data

57.  Inductive learning can be characterized by the
following entailment constraint:
 Hypothesis ^ Descriptions |= Classifications
 given our hypothesis and descriptions of
problem instances, we want to generate
classifications
 This is inductive learning

58. Other kinds of learning that use prior
knowledge are:
1) Explanation based learning (EBL)
2) Relevance based learning
3) Knowledge based inductive learning

59. 1) Explanation based
learning(EBL)
 this kind of learning occurs when the system finds
an explanation of an instance it has seen, and
generalizes the explanation
 The general rule follows logically from the
background knowledge possessed by the system
 The entailment constraints for EBL are
 Hypothesis ^ Descriptions |= Classification
 Background |= Hypothesis

60.  agent does not actually learn anything
factually new, since the hypothesis was
entailed by background knowledge
 This kind of learning is regarded as a way to
convert first principles into useful specialized
knowledge (converting problem-solving search
into pattern-matching search)

61.  basic idea is to construct an explanation of the
observed result, and then generalize the
explanation
 More specifically, while constructing a proof of the
solution, a parallel proof is performed, in which
each constant of the first is made into a variable
 Then a new rule is built in which the left-hand side
is the leaves of the proof tree, and the right-hand
side is the variabilized goal, up to any bindings
that must be made with the generalized proof

62.  Any conditions true regardless of the variables are
dropped
 Note that by pruning the tree before the leaves,
even more general rules may be learned
 However, the more general, the more computation
may be required to apply the rule
 One approach is to require the operationality of
the subgoals in the new rule -- that they be "easy"
to solve

63. 2) Relevance Based Learning
 This is a kind of learning in which background
knowledge relates the relevance of a set of
features in an instance to the general goal
predicate
 For example, if I see men in the Forum in Rome
speaking Latin, and I know that if seeing someone
in a city speaking a language usually means all
people in the city speak that language, I can
conclude Romans speak Latin

64.  In general, background knowledge, together
with the observations, allows the agent to form
a new, general rule to explain the observations
 The entailment constraint for RBL is
 Hypothesis ^ Descriptions |= Classifications
 Background ^ Descriptions ^ Classifications |=
Hypothesis

65.  This is a deductive form of learning, because it cannot
produce hypotheses that go beyond the background
knowledge and observations
 We presume that our knowledge base has a set of
functional dependencies or determiners that support
the construction of hypotheses
 The learning algorithm then tries to find the minimal
consistent determination (e.g., a sentence of the form
"P determines Q," meaning that if the examples match
on P they match on Q)

66. 3) Knowledge based inductive
learning
 This is a kind of learning in which our background
knowledge, together with our observations, lead
us to make a hypothesis that explains the
examples we see
 If I see the Old Man from Scene 24 on the Bridge
of Despair, and notice that he asks a simple
question of every other knight that attempts to
cross, I can hypothesize that only the odd-
numbered knights are able to cross the Gorge of
Eternal Peril

67.  The entailment constraint in this case is
 Background ^ Hypothesis ^ Descriptions |=
Classifications
 Such knowledge-based inductive learning has
been studied mainly in the field of inductive
logic programming

68.  Such systems reduce learning complexity in
two ways
 First, by requiring all new hypotheses to be
consistent with existing knowledge, they reduce
the search space of hypotheses
 Secondly, the more prior knowledge available,
the less new knowledge required in the
hypothesis to explain the observations

69.  Attribute-based learning algorithms are
incapable of learning predicates
 One of the advantages of ILP algorithms is
their much broader range of applicability

70. Instance Based Learning
(IBL)

71. Background
 Storing and using specific instances improves
the performance of several supervised
learning algorithm
 Include algorithms that learn decision trees,
classification rules, and distributed networks
 IBL algorithms are derived from the nearest
neighbor pattern classifier

72. Instance based learning
 generates classification predictions using only
specific instances
 do not maintain a set of abstractions derived from
specific instances
 This approach extends the nearest neighbor
algorithm, which has large storage requirements
 storage requirements can be significantly reduced
with, at most, minor sacrifices in learning rate and
classification accuracy

73.  While the storage-reducing algorithm performs
well on several real world databases, its
performance degrades rapidly with the level of
attribute noise in training instances
 save and use only selected instances to
generate classification predictions

74. Using specific instances in
supervised learning algorithms
 decreases the costs incurred
 when updating concept descriptions, increases
learning rates,
 allows for the representation of probabilistic
concept descriptions,
 and focuses theory-based reasoning in real-
world applications

75. Instance-based learning algorithms
suffer from several problems
 they are computationally expensive classifiers since
they save all training instances,
 they are intolerant of attribute noise,
 they are intolerant of irrelevant attributes,
 they are sensitive to the choice of the algorithm's
similarity function,
 there is no natural way to work with nominal-valued
attributes or missing attributes, and
 they provide little usable information regarding the
structure of the data

76. Overview of IBL
 Learning task : supervised learning or learning
from examples
 Only input is a sequence of instances
 Each instance is assumed to be represented by a
set of attribute-value pairs (?? Next slide)
 All instances are assumed to be described by the
same set of n attributes, although this restriction is
not required by the paradigm itself (Aha, 1989c)
and missing attribute values are tolerated

77. What are attribute-value pairs?
 An action-value function assigns an expected
utility to the result of performing a given action in a
given state
 If Q(a, i) is the value of doing action a in state i,
then
 U(i) = maxa Q(a, i)
 The equations for Q-learning are similar to those
for state-based learning agents

78.  The difference is that Q-learning agents do not
need models of the world. The equilibrium
equation, which can be used directly (as with
ADP agents) is
 Q(a, i) = R(i) + SUMj Ma
ij maxa' Q(a', j)
 The temporal difference version does not
require that a model be learned; its update
equation is

79. About attributes
 set of attributes defines an n-dimensional instance
space
 Exactly one of these attributes corresponds to the
category attribute;
 the other attributes are predictor attributes
 A category is the set of all instances in an
instance space that have the same value for their
category attribute

80. IBL
 IBL algorithms can learn multiple, possibly
overlapping concept descriptions simultaneously
 primary output of IBL algorithms is a concept
description (or concept)
 This is a function that maps instances to
categories: given an instance drawn from the
instance space, it yields a classification, which is
the predicted value for this instance's category
attribute

81.  An instance-based concept description includes a
set of stored instances and, possibly, some
information concerning their past performances
during classification
 e.g., their number of correct and incorrect
classification predictions
 This set of instances can change after each
training instance is processed

82.  However, IBL algorithms do not construct
extensional concept descriptions
 Instead, concept descriptions are determined
by how the IBL algorithm's selected similarity
and classification functions use the current set
of saved instances

83. IBL framework components
 Similarity Function:
 This computes the similarity between a training
instance i and the instances in the concept
description
 Similarities are numeric-valued

84.  Classification Function:
 This receives the similarity function's results and
the classification performance records of the
instances in the concept description
 It yields a classification for i

85.  Concept Description Updater:
 This maintains records on classification
performance and decides which instances to
include in the concept description
 Inputs include i, the similarity results, the
classification results, and a current concept
description
 It yields the modified concept description.

86.  The similarity and classification functions
determine how the set of saved instances in
the concept description are used to predict
values for the category attribute
 Therefore, IBL concept descriptions not only
contain a set of instances, but also include
these two functions.

87.  IBL algorithms assume that similar instances have
similar classifications
 This leads to their local bias for classifying novel
instances according to their most similar neighbor's
classification
 IBL algorithms also assume that, without prior
knowledge, attributes will have equal relevance for
classification decisions (i.e., by having equal weight in
the similarity function)
 This bias is achieved by normalizing each attribute's
range of possible values

88. Summary
 IBL algorithms differ from most other supervised
learning methods:
 they don't construct explicit abstractions such as
decision trees or rules
 Most learning algorithms derive generalizations
from instances when they are presented and use
simple matching procedures to classify
subsequently presented instances

89. Performance Dimensions
 1) Generality: This is the class of concepts which
are describable by the representation and
learnable by the algorithm
 We will show that IBL algorithms can pac-learn
(Valiant, 1984) any concept whose boundary is a
union of a finite number of closed hyper-curves of
finite size
 2) Accuracy: This is the concept descriptions'
classification accuracy.

90.  3) Learning Rate: This is the speed at which
classification accuracy increases during training
 It is a more useful indicator of the performance of the
learning algorithm than is accuracy for finite-sized training
sets
 4) Incorporation Costs: These are incurred while
updating the concept descriptions with a single
training instance
 They include classification costs
 5) Storage Requirement: This is the size of the

91. IBL algorithm

93. THANK YOU