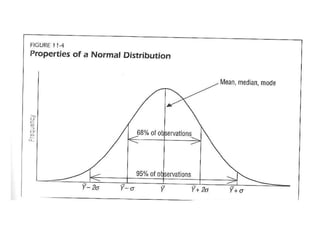
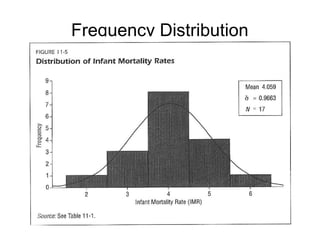
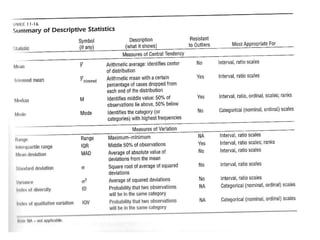
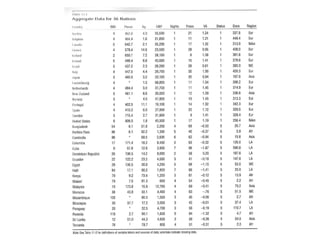
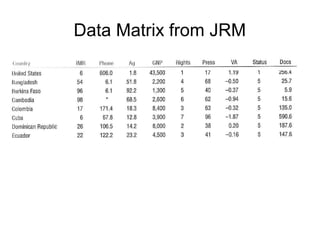
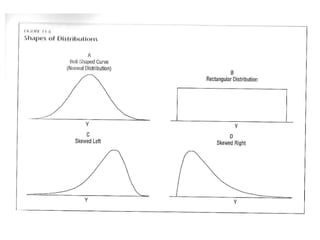
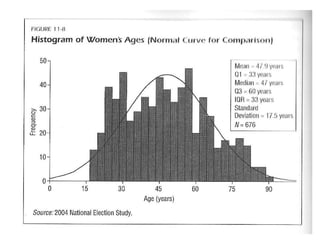
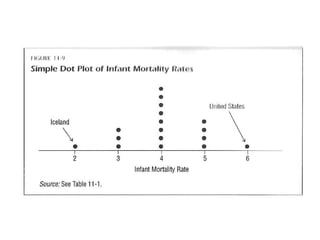
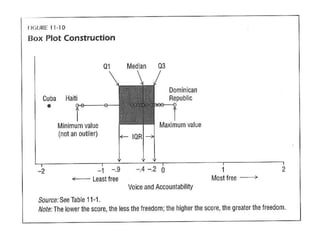
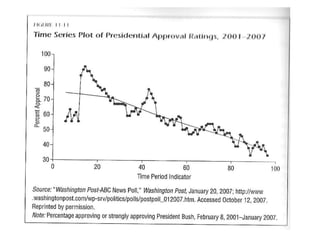
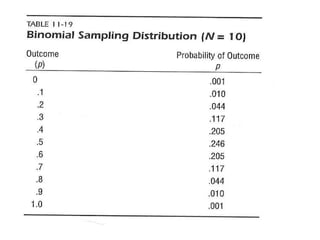
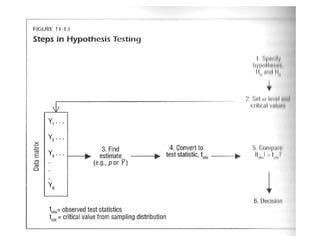
The document provides an overview of key statistical concepts including variance, standard deviation, the normal distribution, frequency distributions, data matrices, hypothesis testing, and point and interval estimation. Variance and standard deviation are measures of how dispersed data points are around the mean. The normal distribution is symmetric and bell-shaped. Hypothesis testing involves specifying a null hypothesis, alternative hypothesis, test statistic, decision rule, and critical region to determine whether to reject the null hypothesis. Point and interval estimation aims to estimate population parameters from samples and provide confidence intervals.

1. Statistics: First Steps
Andrew Martin
PS 372
University of Kentucky

2. Variance
Variance is a measure of dispersion of data
points about the mean for interval- and ratio-level
data.
Variance is a fundamental concept that social
scientists seek to explain in the dependent
variable.

4. Standard Deviation
Standard deviation is a measure of dispersion of
data points about the mean for interval- and ratio-
level data.
Like the mean, standard deviation is sensitive to
extreme values.
Standard deviation is calculated as the square
root of the variance.

7. Normal Distribution

The bulk of observations lie in the center,
where there is a single peak.

In a normal distribution half (50 percent) of the
observations lie above the mean and half lie
below it.

The mean, median and mode have the same
statistical values.

Fewer and fewer observations fall in the tails.

The spread of the distribution is symmetric.

8. Normal Distribution

Mathematical theory allows us to know what
percentage of observations lie within one
(68%), two (95%) or three (98%) standard
deviations of the mean.

If data are not perfectly normally distributed, the
percentages will only be approximations.

Many naturally occurring variables do have
nearly normal distributions.

Some can be transformed using logarithms.

9. Frequency Distribution

10. What about categorical variables?

12. Example
Calculate the ID and IQV for a former PS 372
class grades using the following frequencies or
proportions:
Grade Freq. Prop.
A 4 (.12)
B 7 (.21)
C 4 (.12)
D 7 (.21)
E 12 (.34)

13. Index of Diversity
ID = 1 – (p2
a
+ p2
b
+ p2
c
+p2
d
+p2
e
)
ID = 1 - (.122
+ .212
+ .122
+ .212
+ .342
)
ID = 1 - (.0144 + .0441 + .0144 + .0441 + .1156)
ID = 1 - (.2326)
ID = .7674

14. Index of Qualitative Variation
1 – (p2
a
+ p2
b
+ p2
c
+p2
d
+p2
e
)
1 - (1/K)

15. Index of Qualitative Variation
.7674
(1 – 1/5)
.9592

17. Data Matrix
A data matrix is an array of rows and columns
that stores the values of a set of variables for all
the cases in a data set.
This is frequently referred to as a dataset.

20. Data Matrix from JRM

21. Properties of Good Graphs
Should answer several of the following questions:
(JRM 384)
1. Where does the center of the distribution lie?
2. How spread out or bunched up are the
observations?
3. Does it have a single peak or more than one?
4. Approximately what proportion of observations
in in the ends of the distributions?

22. Properties of Good Graphs
5. Do observations tend to pile up at one end of
the measurement scale, with relatively few
observations at the other end?
6. Are there values that, compared with most,
seem very large or very small?
7. How does one distribution compare to another
in terms of shape, spread, and central tendency?
8. Do values of one variable seem related to
another variable?

28. Statistical Concepts
Let's quickly review some concepts.

29. Population
A population refers to any well-defined set of
objects such as people, countries, states,
organizations, and so on. The term doesn't simply
mean the population of the United States or some
other geographical area.

30. Population

A sample is a subset of the population.

Samples are drawn in some known manner and
each case is chosen independently of the other.

From here on out, when the book uses the term
sample, random sample or simple random
sample, it's making reference to the same
concept, which is a sample chosen at random.

31. Populations

Parameters are numerical features of a
population.

A sample statistic is an estimator that
corresponds to a population parameter of
interest and is used to estimate the population
value.

Y is the sample mean, (μ) is the population
mean.

^ is a “hat”, caret or circumflex

32. Two Kinds of Inference
Hypothesis Testing
Point and interval estimation

33. Hypothesis Testing
Many claims can be translated into specific
statements about a population that can be
confirmed or disconfirmed with the aid of
probability theory.
Ex: There is no ideological difference between the
voting patterns between the voting patterns of
Republican and Democrat justices on the U.S.
Supreme Court.

34. Point and Interval Estimation
The goal here is to estimate unknown population
parameters from samples and to surround those
estimates with confidence intervals. Confidence
intervals suggest the estimates reliability or
precision.

35. Hypothesis Testing
Start with a specific verbal claim or proposition.
Ex: The chances of getting heads or tails when
flipping the coin is are roughly the same.
Ex: The chances of the United States electing a
Republican or Democrat president are roughly the
same.

36. Hypothesis Testing

37. Hypothesis Testing
Next, the researcher constructs a null hypothesis.
A null hypothesis is a statement that a
population parameter equals a specific value.

38. Hypothesis Testing
Following up on the coin example, the null
hypothesis would equal .5.
Stated more formally: H0
: P = .5
Where P stands for the probability that the coin
will be heads when tossed.
H0
is typically used to denote a null hypothesis.

39. Hypothesis Testing

Next, specify an alternative hypothesis.

An alternative hypothesis is a statement
about the value or values of a population
parameter. It is proposed as an alternative to
the null hypothesis.

An alternative hypothesis can merely state that
the population does not equal the null
hypothesis, or is greater than or less than the
null hypothesis.

40. Hypothesis Testing
Suppose you believe the coin is unfair, but have
no intuition about whether it is too prone to come
up heads or tails.
Stated formally, the alternative hypothesis is:
HA
: P ≠ .5

41. Hypothesis Testing
Perhaps you believe the coin is more likely to
come up heads than tails. You would formulate
the following alternative hypothesis:
HA
: P > .5
Conversely, if you believe the coin is less likely to
come up heads than tails, you would formulate
the alternative hypothesis in the opposite
direction:
HA
: P < .5

42. Hypothesis Testing

After specifying the null and alternative
hypothesis, identify the sample estimator that
corresponds to the parameter in question.

The sample must come from the data, which in
this case is generated by flipping a coin.

43. Hypothesis Testing

Next, determine how the sample statistic is
distributed in repeated random samples. That
is, specify the sampling distribution of the
estimator.

For example, what are the chances of getting
10 heads in 10 flips (p = 1.)? What about 9
heads in 10 flips (p = .9)? 8 flips (p = .8)?

45. Hypothesis Testing

Make a decision rule based on some criterion
of probability or likelihood.

In social sciences, a result that occurs with a
probability of .05 (that is, 1 chance in 20) is
considered unusual and consequently is
grounds for rejecting a null hypothesis.

Other common thresholds (.01, .001) are also
common..

Make the decision rule before collecting data.

46. Hypothesis Testing

In light of the decision rule, define a critical
region. The critical region consists of those
outcomes so unlikely to occur that one has
cause to reject the null hypothesis should they
occur.

So there are areas of “rejection” (critical areas)
and nonrejection.

48. Hypothesis Testing

Collect a random sample and calculate the
sample estimator.

Calculate the observed test statistic. A test
statistic converts the sample result into a
number that can be compared with the critical
values specified by your decision rule and
critical values.

Examine the observed test statistic to see if it
falls in the critical region.

Make practical or theoretical interpretation of
the findings.