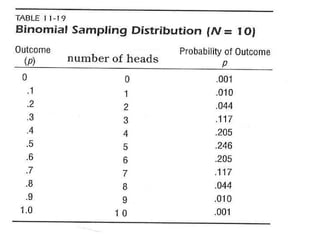
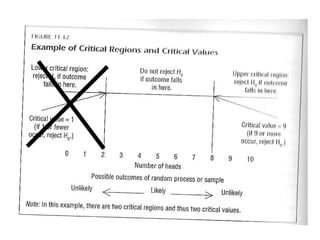
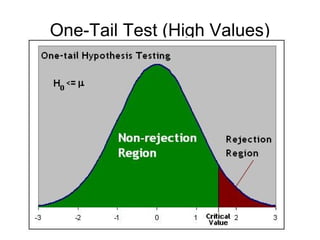
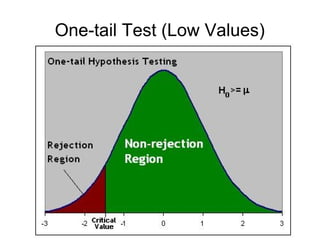
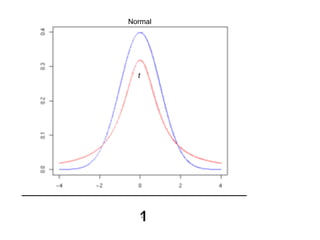
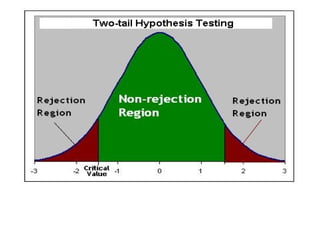
1) The document discusses hypothesis testing and statistical inference using examples related to coin tossing. It explains the concepts of type I and type II errors and how hypothesis tests are conducted. 2) An example is provided to test the hypothesis that the average American ideology is somewhat conservative (H0: μ = 5) using data from the National Election Study. The alternative hypothesis is that the average is less than 5 (HA: μ < 5). 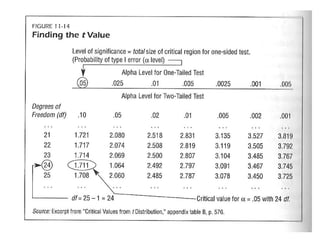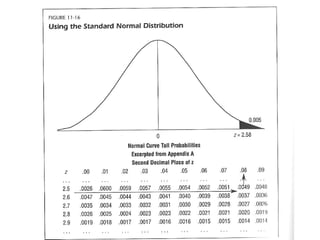3) The results of the hypothesis test show the observed test statistic is lower than the critical value, so the null hypothesis that the average is 5 is rejected in favor of the alternative that the average is less than 5.

1. More Statistics
Andrew Martin
PS 372
University of Kentucky

2. Inference
Inference refers to reasoning from available
information or facts to reach a conclusion.
However, there is no guarantee the inference is
correct.
In fact, inferences are sometimes incorrect.

3. Inference
In statistical inference the estimated values of
unknown population parameters are sometimes
incorrect.
Concerning hypothesis testing, there are two
types of mistakes we can make: a Type I error
and a Type II error.

4. Type I Error
Type I error occurs whenever one rejects a true null
hypothesis.
Suppose:
(1) in reality, the coin is fair (that is, H0
: P = .5)
(2) You decide to reject H0
if 0,1,9 or 10 heads occurs.
(3) your opponent obtains 9 heads in 10 tosses.
(4) You reject the hypothesis and accuse the
person of being unfair.

5. Type II Error

Type II error occurs whenever one fails to
reject a false null hypothesis.
Suppose:
(1) in reality, the coin is unfair (that is, H0
: P = .9)
(2) You decide to reject H0
only if 10 heads occurs.
(3) Your opponent obtains 9 heads in 10 tosses.
(4) You do not reject the null hypothesis (H0
: P = .5)
even though it is false.

6. What are the chances?
The probability of committing a type I error is the
“size” of the critical region. It is designated by small
Greek letter alpha (α).
The probability of committing a type II error (β)
depends on :
1) how far the true value of the population parameter is
from the hypothesized one
2) the sample size – the larger the sample size, the
lower the probability of committing a type II error.

8. Standard Error
Imagine taking an endless number of independent
samples of size N from a fixed population that has a
mean of μ and a standard deviation σ.
For each sample, you calculate Y
and the standard deviation
¿
¿
σ

9. Standard Error
The standard deviation of the sampling
distribution is called the standard error of the
mean, or standard error.
Where is the sample standard deviation and N
is the sample size.
σ

10. Standard Error
The expression implies that as the sample size
gets larger and lagers, the standard error
decreases in numerical value.
As a result, as the sample increases we expect Y
to get closer and closer to the true value (μ)

11. Binomial Distributions
Binomial distributions can be used to show how
probabilities can be used to assess the
likelihood that an event will or will not occur
given N observations.
Sometimes an event happening or not happening
is referred to in terms of successes and failures.

12. Binomial Distribution
Coin tosses are a perfect example, because you
can specify tossing heads or tossing heads as
an event. Sticking with heads as the event, it
either happens or fails to happen.

14. Critical Regions and Values
If we have established a critical region such that
we will reject the null hypothesis at 0, 1, 9 or 10
heads, then the size of the critical region would
be calculated as follows:
p0
+ p1
+ p9
+ p10
= α (Critical region)
.001 + .01 + .01 + .001 = .022
So we have .022, or just a little more than 2 out of
100 chances of incorrectly rejecting the null
hypothesis.

15. Critical Regions and Values
On a practical level, the only way one would reject
the null hypothesis (H0
: P = .5) is if in 10 tosses
only 1,2,9 or 10 came up heads – none of which
is likely with a fair coin.

16. Critical Regions and Values
In political science, the critical regions are
typically referred to as levels. In other words, if α
= .05 one would typically say “The null
hypothesis can be rejected at the .05 level.”
This measure specifies the probability of making a
Type I error (rejecting a true null hypothesis).
This concept is also known as statistical
significance.

17. Statistical Significance

The three most common levels of significance
in political science are .05, .01 and .001.

Sometimes scholars use a looser standard of .
10, .05 and .01.

Are these levels appropriate for the discipline?

18. One- or Two-Sided Tests

What if you suspect the null hypothesis is
false? How would you go about formulating an
alternative hypothesis?

Let's return to the coin tossing example. If I
notice a coin tends to come up heads more
likely than tails, I might propose HA
: P > .5 as an
alternative. This is different than merely
assuming HA
: P ≠ .5 because prior observation
tells me there is a directional assumption that
can be made. I'm not too worried that HA
: P < .5

19. One- or Two-Sided Tests

If testing a hypothesis theoretically suggests
only upper or only lower values are relevant, a
one-tail test will suffice.

In other words, a one-tail test requires only one
critical region or value.
 To return to the coin tossing example, if my HA
:
P > .5 I will only be interested in the critical
region where I get 9 or 10 heads out of 10
tosses, and therefore only interested in the
critical value for the upper tail of the distribution.

21. One-Tail Test (High Values)

22. One-tail Test (Low Values)

23. One- or Two-Sided Tests

However, if I have to no reason to suspect large
or small values of P, then I should use a two-tail
test. .
 In other words, if HA
: P ≠ .5, I have no intuition
about whether the probability is higher or lower
than .5, so I use a two-tail test.

25. What about real-world outcomes?

We obviously do not live in a binomial world.

Usually we have to accept more than two
possible outcomes. As a result, a probability
distribution would be increasingly difficult to
tabulate.

Therefore, we cannot compare sample value to
some critical value obtained from some
distribution (such as the binomial distribution).

26. Types of Distributions
Discrete probability distribution
Continuous probability distribution

27. Discrete vs. Continuous
Distributions (Kmenta 1986)

In discrete probability distributions the
elements of sample space are represented by
points that are separated by finite distances.

To each point we can ascribe a numerical value
and to each value we can ascribe a given
probability. (Ex: Coin toss (or binomial
distribution), playing cards, lottery)

However, there are many distributions for which
the sample space does not consist of countable
points but covers and entire interval (or
collection of intervals). These are known as
continuous probability distributions.

28. Discrete Distribution

29. Continuous Distribution

30. Observed Test Statistic
Observed test statistic =
Sample estimate – hypothesized pop. parameter
Standard error
− The observed test statistic is compared to a
critical value, and the decision to reject or not
reject the null hypothesis depends on the
outcome of the comparison.

31. Observed Test Statistic
1. If the observed statistic's value is greater than
or equal to the critical value, reject the null
hypothesis in favor of the alternative.
2. Otherwise, do not reject the null hypothesis.

32. Example of hypothesis testing
Example: Someone tells you “The average
American has left the middle of the road and
now tends to be somewhat conservative.” (H0
:
μ = 5)
You, however, are not so sure. In light of Obama's
recent election, you think America is not
conservative. You believe it to be at least middle
of the road. (HA
: μ < 5)

33. Example of hypothesis testing
Suppose you and your opponent decide to test
these competing claims by examining mean
voter ideology from the National Election Study
(NES), which uses the following scale:
1 – Extremely liberal
2 – Very liberal
3 – Somewhat liberal
4 – Moderate
5 – Somewhat conservative
6 – Very conservative
7 – Extremely conservative

34. Example of hypothesis testing
1 – Extremely liberal
2 – Very liberal
3 – Somewhat liberal
4 – Moderate
5 – Somewhat conservative (opponent's claim)
6 – Very conservative
7 – Extremely conservative
H0
: μ = 5 – opponent's claim
HA
: μ < 5 – your claim (μ is between 1 and 4)

35. Example of hypothesis testing

Before we start, we must decide on the size of
the critical region. Let's set α = .05 (level of
significance).

Next, we must specify the appropriate sampling
distribution.

In a small sample (less than 25 observations)
statistical theory asserts the appropriate
sampling distribution fir a test about the mean is
the t distribution.

36. The t distribution

The t distribution resembles a normal
distribution but is a bit “fatter” in that it has more
area in its tails.

The t distribution depends on the size of the
sample (N). As N gets larger, the t distribution
approaches the shape of the normal
distribution; at N = 30 or N = 40 they are
essentially indistinguishable.

In other words, use the t distribution if the
sample is smaller than 30 or 40; use the normal
distribution if N > 40.

37. t
Normal

39. To use a t distribution ...
1. Determine the size of the sample to be
collected (rule of 30).
2. Find the degrees of freedom (df) by calculating
N-1. Will explain df later.
3. Choose level of significance and directionality
of the test, a one- or two-tailed test at the α
level.
4. Given these choices, find the critical values
located in Appendix B (for t distribution) in JRM
pp. 576.

40. To use a t distribution ...
At this point you would now collect the sample
data, find the sample mean and compute the
observed test statistic (which in this case is a t-
score).
The calculated t-score for the observations is then
compared to a critical value t-score.

41. To use a t distribution ...
If the absolute value of the t-score for the
observations is greater than the t-score for the
critical values, reject H0. Otherwise, do not
reject.
If |tobs
| ≥ tcrit
reject H0
If |tobs
| < tcrit
do not reject H0

42. To use a t distribution ...
is the sample mean
is the hypothesized population mean
is the sample standard deviation
is the sample size

43. To use a t distribution ...
1. Sample size: N = 25.
2. Degrees of freedom (N-1) = 25 – 1 = 24.
3. One-tailed test; α = .05 (level of significance).
4. Look up the corresponding row for degrees of
freedom and column for level of significance in
Appendix B for t distributions on page 576 to get
the corresponding critical value.

45. To use a t distribution ...
Now calculate the t-score for the observations. In
order to make the calculation we need the four
following pieces of information: the sample
mean, hypothesized population mean, sample
standard deviation and sample size.
4.44 is the sample mean
5 is the hypothesized population mean
1.23 is the sample standard deviation
25 is the sample size

47. To use a t distribution ...
The observed t-score is -2.28. The critical value t-
score is 1.711.
Again, if |tobs
| ≥ tcrit
reject H0
Since |-2.28| ≥ 1.711, H0
is rejected.

48. P-Values
The p-value tells you the probability of getting a t
statistic at least as large as the one actually
observed if the null hypothesis is true.
In this sample, the p-value is .016, which tells you
the probability of getting a t statistic at least as
large as the one actually observed if the null
hypothesis is true.
In this sample there is only 1.6 percent chance of
observing a as large as 4.44 if the population
parameter is 5.

50. What about large samples?
Large samples rely on the standard or normal
distribution, but how is the test statistic
calculated?
The test statistic for a normal distribution is known
as a z score, which is the number of standard
deviations by which a score deviates from the
mean score.
For example, z = 1.96 means 1.96 standard
deviations above the mean.

51. How is a z-score calculated?

Z scores are calculated the the same way as t
scores.

However, one has to use a different table to
identify the appropriate critical value. The table
for normal distributions (z scores) is Appendix A
(JRM p. 575)

52. Example in Practice

Let's return to the ideology example. Let's
assume we want to test the assumption that the
United States has become a slightly
conservative country according to the mean
response in the NES (H0
: μ = 5).

This time, however, you have no inclination
about whether the null hypothesis is too
conservative or too liberal. On the one hand, a
fairly liberal presidential candidate just won the
election, but on the other the United States has
always been more conservative than most
advanced industrial democracies (HA
: μ ≠ 5)

53. Example in Practice

Suppose we wanted a higher level of
confidence. This time, we set the size of the
critical region or probability to .01 (or α = .01)

Remember, the alternative hypothesis does not
specify a relationship (that is, no less than or
greater than).

Do we need a one- or two-tail test?

54. Example in Practice

Two-tail test.

Whenever looking up the corresponding z score
for a critical region with a two-tail test, one has
to divide the size of the critical region (here, .
01) by 2.

So, .01/2 = .005.

.005 is the size of the critical region in each tail.

In total, the critical region is .01, giving us a 99
percent level of confidence.

There is only a 1 % chance of committing a
Type I error.

55. To recap ....
If |zobs
| ≥ zcrit
reject H0
If |zobs
| < zcrit
do not reject H0

58. To use the z-score table ....

Notice how the values are arranged from
largest to smallest, descending as you go
across each row and continuing in descending
order as you go down a row.

Find the value closest to .005 (Hint: It's .0049
on the table)

Add the number in the corresponding far left
end of the row to the “second decimal place of
Z” number at the top of the critical value's
column.

For .0049, these numbers are 2.5 + .08, so
2.58 is the critical value of Z.

59. Since | -15.21 | > 2.58 we can reject the null hypothesis
with 99 percent confidence.
In other words, there's only a 1 % chance the null
hypothesis is true. Put yet another way, the chance that
the true population parameter for ideology being 5 is very
small.

60. So what does this tell us?

The sample mean is 4.27, which is still in a
slightly conservative direction.

In interpreting this statistic, a political scientist
may conclude the United States is middle the
road or perhaps slightly conservative, but not
somewhat conservative (μ = 5).

61. Difference between t and z scores

t scores are used for samples of 30 or less; z
scores for samples of more than 30.

t scores require us to calculate degrees of
freedom; z scores do not require such a
calculation.

The bigger the sample size, the smaller the size
of the critical region for both t and z scores.

63. Example in Practice