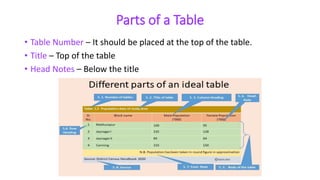
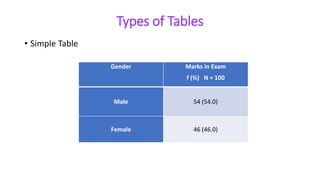
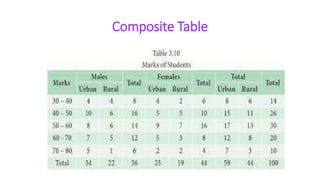
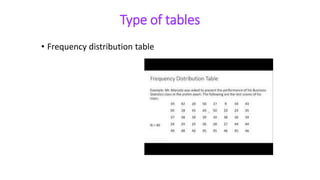
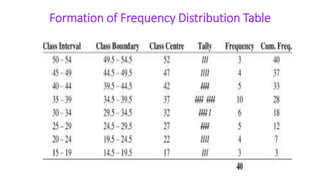
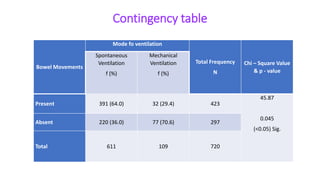
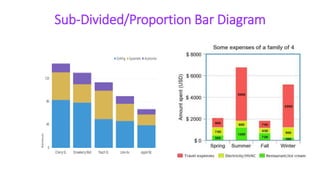
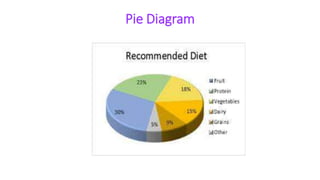
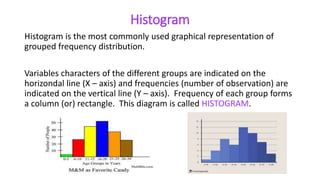
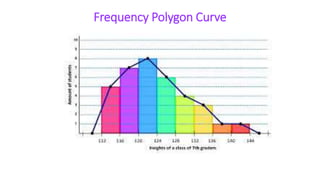
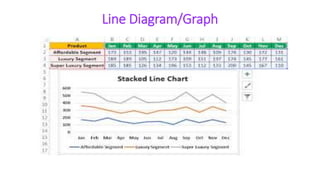
This document provides an overview of statistics and its uses. It discusses how statistics is the study of collecting, analyzing, and presenting data. It then describes some common uses of statistics like simplifying data, facilitating comparisons, and testing hypotheses. The document also lists some key terms in statistics and different types of data. It discusses different types of statistical analyses like descriptive statistics, inferential statistics, and frequencies distributions. Finally, it provides examples of common ways to visually represent data through tables, bar graphs, pie charts, histograms, and other diagrams.

1. STATISTICS
(Introductory Statistics)
Dr. Senthilvel Vasudevan, M.Sc., M.Phil, DST, PGDBS, Ph.D.,
Fellow of Royal Statistical Society (London), MISMS, IAPSM, IPHA, NIN, IMS, IBMS, ISI
Assistant Professor of Statistics (Biostatistics),
Department of Community Medicine,
Sri Venkateshwaraa Medical College Hospital & Research Centre,
Ariyur, Pondicherry – 605 110.
Email ID: senthilvel99@gmail.com

2. Definition of Statistics & Its uses
Statistics is the study of the collection, analysis,
interpretation, presentation, and organization of
data.
Uses of Statistics:
oStatistics presents facts in a definite form
oIt facilitates comparisons
oIt simplifies the masses of figures
oIt helps in formulating and testing hypothesis
oIt helps in prediction

3. Statistics and its tools used in various sectors
Statistics is a tool, and it is used in any fields then it will take its own in
the field.
• Biostatistics – Medicine
• Educational Statistics – Education
• Agricultural Statistics – Agriculture
• Econometrics – Economics
• Mathematical Statistics – Mathematics
• Public Health Statistics – Public Health
and so on………

4. Applications of Statistics
Applications of Statistics in health statistics as follows:
o Defining normal and not normal in context of various aspects related
to health and illness.
o Establishing the accuracy of diagnostic procedures
o Planning of experiments and analysis of results.
o Observations on the natural history of a disease, namely its signs,
symptoms, course, variations and etc.
o Assessment of treatment protocol and different interventions used
for care and treatment
o Collection, analysis, and dissemination of various population health
statistics.

5. Terms Related to Statistics
• Data: A set of values recorded on one or more observations units (or) the
factual information collected during research studies.
• Quantitative Data: Discrete Data (data in whole number – blood sugar, no
of family members) and Continuous Data (Data which can be measured in
fractional values. Ex: Height, Weight, body Temp.
• Qualitative Data: The variables that yield observations on which
individuals can be categorized according to certain characteristics. Ex:
gender, occupation, marital status, and educational status/level.
• Parameters: Characteristics of a population (Ex: Average age of all nurses
in Pondicherry Union Territory)
• Parametric Tests: Statistical tests that involve assumption about the
distribution of the variables and estimation of a parameter.
• Non-Parametric Tests: It doesn’t involve assumptions about distribution.

6. Scales of Measurement
 Quantitative Data (interval – Age Range and ratio –
Height, Weight)
Data 
 Qualitative Data (Nominal - Types of Commodities and
Categorical/ordinal – Income Status )

7. Classification of Statistics
Statistics is mainly divided into two categories.
1. Descriptive Statistics; 2. Inferential Statistics
Descriptive Statistics: It deals with the enumeration, organization, and
graphical representation of data.
Inferential Statistics: It provides the procedures to draw an inference
about the conditions that exist in a large set of observations, that is an
entire population from study of a part of that set (sample).
This branch of statistics is also known as “Sampling Statistics”
(The corresponding statistical tests will be seen afterwards)

8. Descriptive Statistics
Descriptive Statistics is divided into as following ways:
• Measures of data condensation: Frequency distribution and graphical
presentation of data.
• Measures of Central Tendency
• Measures of Dispersion
• Measures of relationship (Correlation Co-efficient)

9. Frequency Distribution
• An appropriate presentation of data involves organization of data in
such a manner that meaningful conclusions and inferences can be
drawn to answer the research question.
• Unsorted and ungrouped records don’t allow us to draw clear
conclusion.
• Quantitative data are generally condensed, and frequency
distribution is presented through tables, charts, graphs, and
diagrams.

10. Table
A table presents data in a concise, systematic manner from masses of
statistical data.
General Principles of Tabulation:
• A table should be precise, understandable, and self explanatory.
• Table should have a proper title and it placed at the top of the table.
It should be clear, concise and precisely.
• Rows and columns to be compared with one another should be
brought together.
• The content of the table, as a whole as well as the items in each
column and row, should be defined clearly and fully.

11. Table (Contd…)
• The unit of measurement must be clearly stated.
• Percentage can be given in the parenthesis or can be worked out to
one decimal figure to draw the reader’s attention.
• Totals can be placed at the bottom of the columns.
• Reference symbols can be directly placed beneath the table for
explanatory footnotes.

12. Parts of a Table
• Table Number – It should be placed at the top of the table.
• Title – Top of the table
• Head Notes – Below the title

13. Parts of a table (Contd…)
Captions and Stubs – Captions are the headings designed for vertical
columns and stubs are the headings for horizontal rows.
Body of the table – Arrangement of the data headings designed for
vertical columns and stubs are the headings for horizontal rows.
Foot Notes - Characteristics or items of the table are not adequately
explained, then footnotes are used to explain those items.
Source Note – When we use the secondary data then we have to
mention the source from which the data for the table or the table itself
is retrieved.

14. Types of Tables
• Simple Table
Gender Marks in Exam
f (%) N = 100
Male 54 (54.0)
Female 46 (46.0)

15. Composite Table

16. Type of tables
• Frequency distribution table

17. Formation of Frequency Distribution Table

18. Contingency table
Bowel Movements
Mode fo ventilation
Total Frequency
N
Chi – Square Value
& p - value
Spontaneous
Ventilation
f (%)
Mechanical
Ventilation
f (%)
Present 391 (64.0) 32 (29.4) 423
45.87
0.045
(<0.05) Sig.
Absent 220 (36.0) 77 (70.6) 297
Total 611 109 720

19. Graphical Presentation of Data
Main reasons for using the diagrammatic and graphic representation of
data are as follows:
• Graphical presentation is the most convenient and easy way to present
any data or statistical data.
• It gives the clear view of entire data. Layman is also understood easily.
• It is visually more attractive way than other ways of representing data.
• It is easy to understand and to memorize the data.
• By this anyone compare the data relating to different periods of time of
different origins (or) different regions.

20. Types of Diagrams
• Bar Diagram – Simple, Multiple, Sub-divided
• Pie Chart/Sector diagram
• Histogram
• Frequency Polygon
• Line graphs/diagram
• Cumulative Frequency Curve (or) Ogive
• Scattered Diagram (or) Dotted Diagram
• Pictograms (or) Picture Diagram
• Map Diagram (or) Spot Map

21. Bar Diagram
Bar diagram is a convenient graph that is particularly useful for
displaying nominal (or) ordinal data.

22. Keep in mind at the time of making bar diagram
• The width of the bars should be uniform throughout the diagram
• The gap between the bars should be uniform throughout the
diagram.
• Bars may be vertical (or) horizontal.
There are 3 types of bar diagrams: Simple, Multiple and
Proportion/Sub-divided bar diagram.

23. Multiple Bar Diagram

24. Sub-Divided/Proportion Bar Diagram

25. Pie Diagram/Sector Diagram
Pie diagram is another useful pictorial diagram/device for presenting
discrete data of qualitative characteristics, such as age-groups, gender,
and occupational groups in a population.
The total area of the circle represents the entire data under
consideration. Researcher must remember that only percentage data
must be used to prepare pie diagrams. It gives comparative differences
at a glance. Size of each angle is calculated by multiple class
percentages with 360° degree (or) calculated by the following formula:
Class Frequency
------------------------- X 360°
Total Observation

26. Pie Diagram

27. Histogram
Histogram is the most commonly used graphical representation of
grouped frequency distribution.
Variables characters of the different groups are indicated on the
horizondal line (X – axis) and frequencies (number of observation) are
indicated on the vertical line (Y – axis). Frequency of each group forms
a column (or) rectangle. This diagram is called HISTOGRAM.

28. Frequency Polygon
Frequency polygon curve obtained by joining the middle top points of
the rectangles in a histogram by straight lines.
It can be drawn by using following steps:
• Draw the histogram with the given data
• Join the midpoints of upper horizondal sides of each rectangle with
the adjacent one by a straight line.
• Close the polygon at both ends of the distribution by extending them
to base line.
• Hypothetical classes at each end would have to be included with a
frequency of zero.

29. How to draw a frequency polygons?
• Draw a histogram with the given data
• Join the midpoints of upper horizontal sides of each rectangle with
the adjacent one by a straight line.
• Close the polygon at both endsof the distribution by extending them
to base line.
• Hypothetical classes at each end would have to be included with a
frequency of zero.

30. Frequency Polygon Curve

31. Line Diagram/Graph