Multi-machine stability study using robust AVR-PSS

International Journal of Electrical Engineering and Technology (IJEET), ISSN 0976 – 6545(Print),
ISSN 0976 – 6553(Online) Volume 6, Issue 5, May (2015), pp. 21-29 © IAEME
21
STABILITY STUDY OF A MULTI MACHINE SYSTEM
USING MODIFIED ROBUST CO-ORDINATE AVR AND
POWER SYSTEM STABILIZER
C.R.Dash1
, B.P.Dash2
, R.Behera3
1
Department of Mathematics GCE, Kalahandi, Bhabani Patana
2
Department of Electrical Engineering, KISD, Bhubaneswar
3
Department of Electrical Engineering, IGIT, Sarang, Odisha. (BPUT, Odisha)
ABSTRACT
Modern power system is a complex network. Rapid industrialization & globalization makes
the network management more complex. The stability of power system becomes a more critical
challenge because a cost of a voltage collapse or instability could cause power interupti0n that could
have very high impact on economy. As network expands, generating station in one cluster& the
neighboring cluster can develop oscillatory tendencies under disturbance. This depends on relative
strength of the group of generators& the interconnecting network. The generator could be of
different make, different size & different type of excitation & governor control. This adds to the
complexity of the system as response of different generators could be different. The exhibits low
damping to certain disturbances & resulting oscillation could lead to instability. Power system
stabilizers provide an effective means of improving system damping of electric power system during
low frequency oscillations in the range of 0.5 to 3HZ.Low frequency oscillations are a common
problem in large power system. Low frequency oscillations are observed when large power systems
are interconnected by relatively weak tie lines. These oscillations may sustain & grow to cause
system separation if no adequate damping is available. Excitation control or AVR is well known as
an effective mean to improve the overall stability of the power system. This work is an effort to
ensure quality power to the consumers efficiently by using Robust-co-ordinate AVR-PSS (RCAP).
This work presents the stability study of a Multimachine system using Robust AVR& PSS.
Index terms: Robust, Model, Damping Ratio, Power Angle, Terminal Voltage, Internal Modeling of
Component (IMC), Classical Framework
INTERNATIONAL JOURNAL OF ELECTRICAL ENGINEERING &
TECHNOLOGY (IJEET)
ISSN 0976 – 6545(Print)
ISSN 0976 – 6553(Online)
Volume 6, Issue 5, May (2015), pp. 21-29
© IAEME: www.iaeme.com/IJEET.asp
Journal Impact Factor (2015): 7.7385 (Calculated by GISI)
www.jifactor.com
IJEET
© I A E M E

22
I. INTRODUCTION
In the present power scenario of India, it is being observed that the energy sector is
undergoing a paradegic change due to globalization, deregulation & rapid industrialization. Now it
has become a challenging task for the power industries to deal with the sudden increase in industrial
& domestic loads. The problem becomes more critical when consumers demand quality power.
Quality power involves maintaining constancy of frequency, voltage& power angle. For decades the
stability has been a big challenge for power industries. This work is an effort to maintain the
constancy of voltage, power angle & frequency of a multimachine system. The power demand
usually deviates from its normal value with an unpredictable small amount, causing a change in the
system state. The developed automatic control system must detect these changes &initiate a set of
counter control in real time which can eliminate the state deviations as quickly & effectively as
possible. Application of automatic control technique is feasible if the modeling of a system is
possible. The block diagram model of such a system was first used by Heffron-Phillip &later by
F.P.Demello & C.Concordia. The model includes an automatic voltage regulator (AVR) loop which
controls the magnitude of the terminal voltage .The terminal voltage is continuously sensed,
rectified& smoothed. This dc signal is compared with a dc reference voltage. The resulting error
voltage after amplification signal shaping is fed to the exciter as input. The exciter then controls the
output voltage of the generator. This paper considers the design of AVR&PSS for a Multimachine
power system. The basic function of a pss is to add damping to the generator rotor oscillations by
controlling its excitation using auxiliary signals. To provide damping the stabilizer must produce a
component of electrical torque in phase with the rotor speed deviations. The conventional approach
to AVR-PSS design can basically be classified as a sequential design consisting of two stages.
Firstly, the AVR is designed to meet the required voltage regulation performance. Then, the PSS is
designed to meet the required damping performance. . A practical AVR-PSS must be robust over a
wide range of operating conditions & capable of damping not only a local mode of oscillation but
also the inter-area system modes. The AVR is essentially a first order lag controller while the PSS is
a fixed structure controller consisting of a gain in series with lead-lag networks, generating a
stabilizing signal to modulate the reference of the AVR.K.T.Law, D.J.Hill& N.R.Godfrey in their
paper ‘Robust Co-ordinate AVR-PSS design” proposed two models of RCAP namely (i)RCAP in
IMC framework& (ii)RCAP in classical framework. This work is an expansion of the above model
for a multimachine power system.
II. SELECTION OF POWER SYSTEM STABILIZER MODEL ROBUST COORDINATED
AVR-PSS (RCAP)
A. Conventional AVR-PSS model
The following model shows the first conventional RCAP proposed by deMello and
Concordia in which it is proposed that the gains of AVR and PSS are defined as
1
)(
+
=
v
v
AVR
T
K
sK (1)
n
sPSS
sT
sT
KsK 





+
+
=
1
1
)(
2
1 (2)
∆= ϖPSSU (3)

23
The PSS is tuned to satisfy the following relation
)()( oscoscPSS jGEPjK ϖϖ ∆=∆ (4)
Where GEP∆ the perturbation of GEP is defined in conventional RCAP and oscϖ is the oscillation
frequency
Fig. 1: conventional AVR-PSS model
B. RCAP model in IMC (internal model control) frame work
i) Here the closed loop system has two resonance modes due to the complex poles of the inner
closed loop system after the application of PSS.
ii) the complex poles of the AVR controller Q2
Fig. 2: Robust coordinate AVR-PSS model in internal model control frame
The overall closed loop system responses to all disturbances are dependent on both sets of poles.
It is only logical to coordinate the AVR-PSS so that the damping ratio of the poles in (i) and (ii) are
equal. So the gains Q1 and Q2 may be defined as
)1(
1'3
1
+
+
=
sK
sM
Q
fad
do
λ
τ
(5)
( ) ( ) 











−++++












++





++
=
6
52
1
2
2
2
1
22
2
21
2
M
MM
MsDDHssM
D
K
M
MsD
K
M
DHsK
Q
RAVRv
ad
R
ad
ad
ϖλ
ϖ δω
(6)

24
C. RCAP in classical frame work
Fig. 3: RCAP model in classical frame
The modified model of RCAP in IMC framework is known as RCAP in classical frame work.
It consists of two integrating controllers known as C1 and C2 .Here the anti-windup reset scheme is
used to prevent integral windup. In this model the inner field controller,C1 is a standard PI-controller
and C2 has an integrator to ensure zero steady state error. The transfer functions of C1 and C2 are as
follows
The PSS for the inner loop is given by
R
R
PSS
DsD
C
ϖ
ϖ δω +
=
(7)
sK
sM
C
fad
do
λ
τ 1'3
1
+
=
(8)












−++++












++





++
=
6
52
1
2
6
2
1
22
2
)(2)1(
2
M
MM
MsDDHssM
D
K
M
MsD
K
M
DHsK
C
RAVRv
ad
R
ad
ad
ϖλ
ϖ δω
(9)
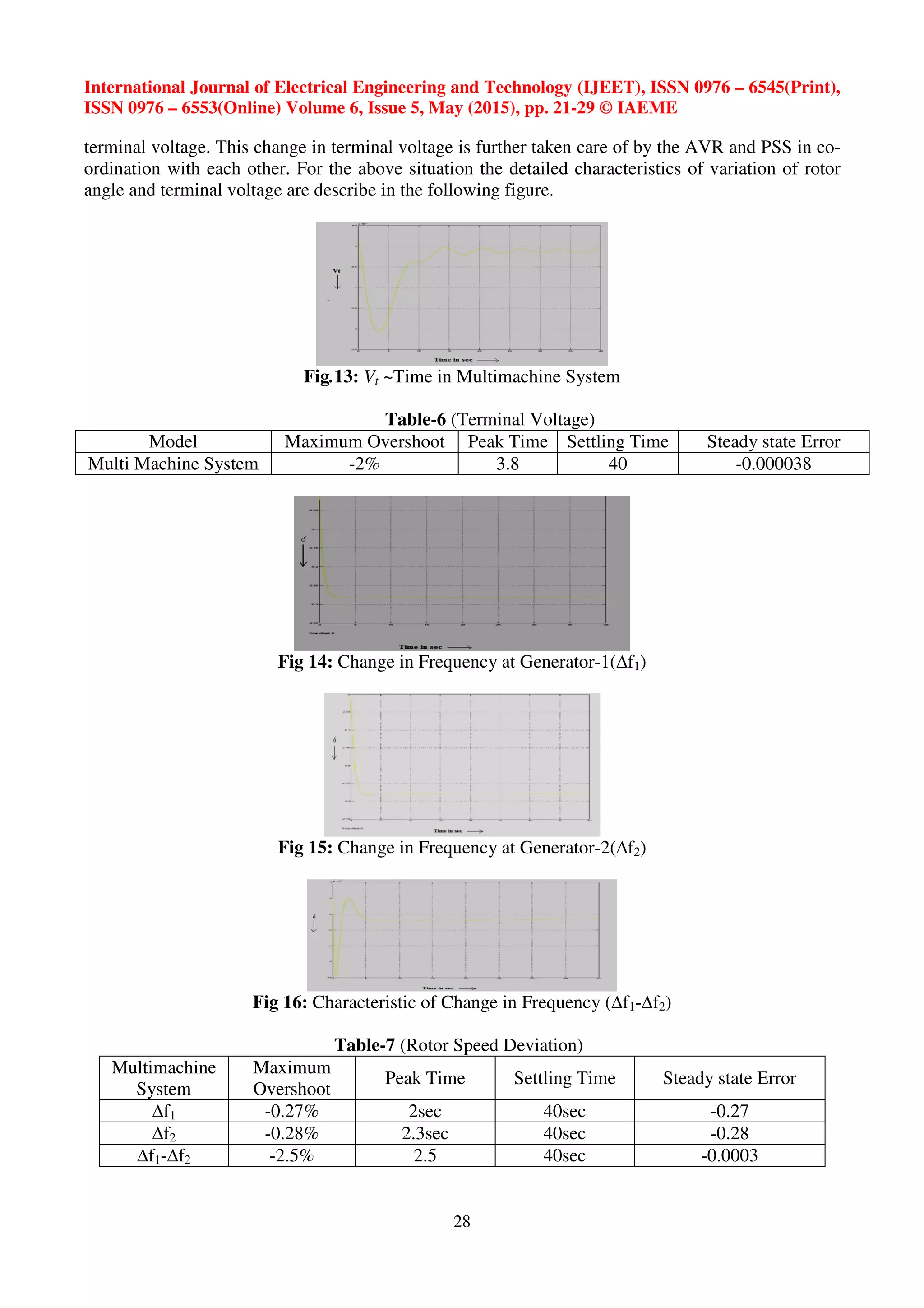
D. RCAP in classical frame work applied to Multimachine System:
Here, a study has been conducted on a Multimachine system using the above model described
in Fig. 4.4. Two machines of equal per unit rating and equal rated turbines connected through a tie-
line has been selected for this purpose. The details of the parameters are described in table [ ]
Fig 4: Block Diagram of Multimachine System
Fig 5: Load Frequency Model of both machines connected Through Tie-line

25
Fig 6: Model for Study of change in rotor angle using the new PSS
Fig 7: Model for Study of change in terminal voltage using the new PSS
III. CASE STUDIES
Case-I: A single machine connected to infinite bus system with the proposed PSS model has been
prepared. This model is described in fig. 4.4. The Generator data is mentioned in Table [5.1]. The
model is simulated in the MATLAB platform.
Case-II: A study has been conducted on a Multimachine system using the above model described in
Fig. 4.4. Two machines of equal per unit rating and equal rated turbines connected through a tie-line
has been selected for this purpose. The details of the parameters are described in table.
RESULTS AND DISCUSSION
A: Case-I:
The performances of CPSS are compared between model of RCAP in IMC frame work and
with model in Classical frame work. The system data are summarized below.
Table-1 (Generator Input data)
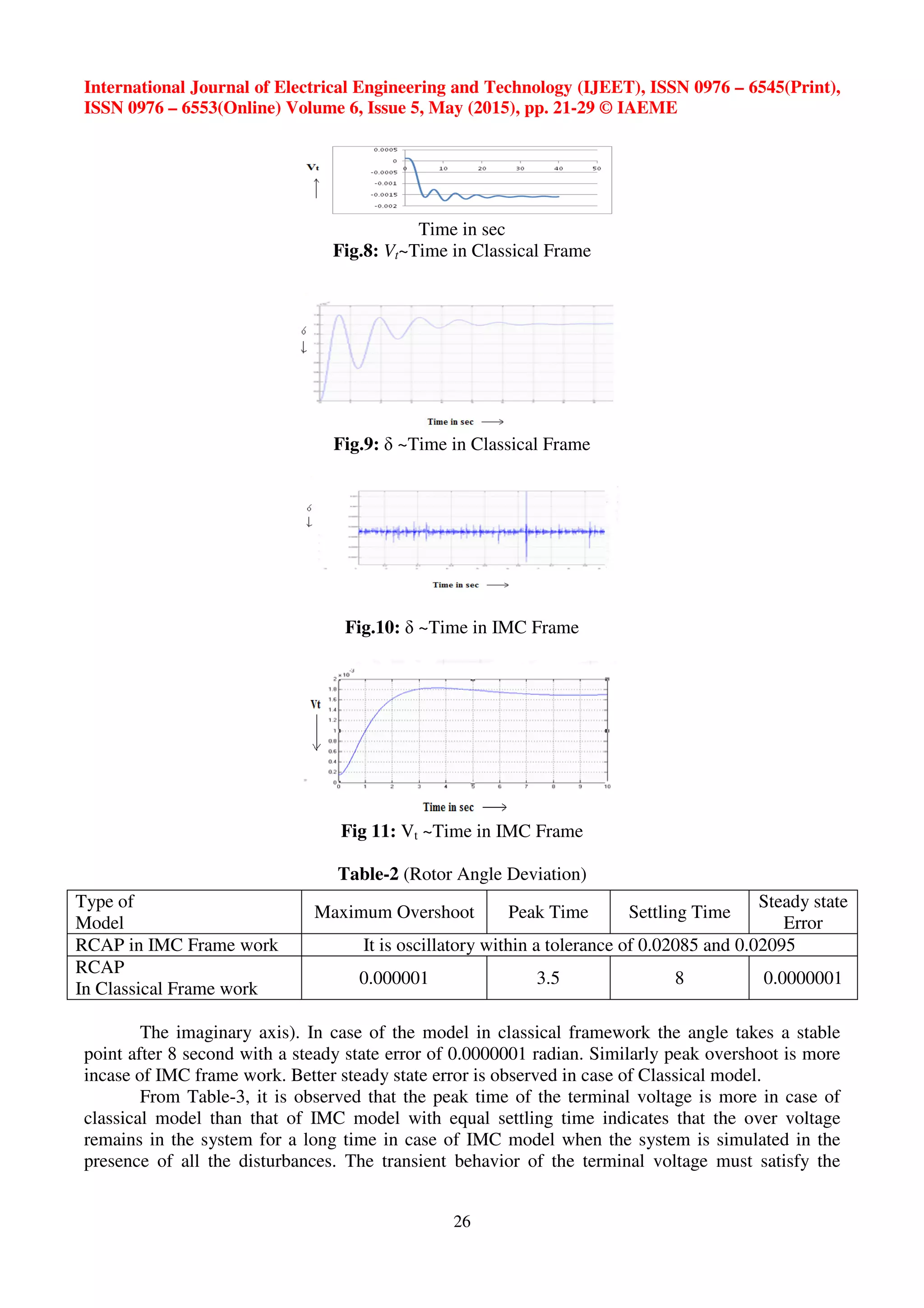
From Table-5.2 it is observed that the peak time for power angle in case of IMC frame work
is faster than that of classical model. As power angle is responsible for power transfer, an oscillatory
response of the same destabilizes the system and questions on the quality power in case of the model
in IMC framework (dominating complex poles are located exactly on
Generator Data H=3.5;Xd=1.81;Xq=1.76;Xd’=0.3;;Xe=0.16;Rfd=0.0006;Re=0.003;
τdo’=8;KD=0;Ladu=1.65;Laqu=1;edo=0.6836;eqo=0.7298;Ido=0.8342;
iqo=0.4518;δo=79.13;Efdo=2.395;Vdo=0.72;Vqo=0.77;Vto=1
Exciters Data Lfd=0.153;Rfd=0.0006;Efdo=2.395
CPSS Data 0.003s-0.187

26
Time in sec
Fig.8: Vt~Time in Classical Frame
Fig.9: δ ~Time in Classical Frame
Fig.10: δ ~Time in IMC Frame
Fig 11: Vt ~Time in IMC Frame
Table-2 (Rotor Angle Deviation)
The imaginary axis). In case of the model in classical framework the angle takes a stable
point after 8 second with a steady state error of 0.0000001 radian. Similarly peak overshoot is more
incase of IMC frame work. Better steady state error is observed in case of Classical model.
From Table-3, it is observed that the peak time of the terminal voltage is more in case of
classical model than that of IMC model with equal settling time indicates that the over voltage
remains in the system for a long time in case of IMC model when the system is simulated in the
presence of all the disturbances. The transient behavior of the terminal voltage must satisfy the
Type of
Model
Maximum Overshoot Peak Time Settling Time
Steady state
Error
RCAP in IMC Frame work It is oscillatory within a tolerance of 0.02085 and 0.02095
RCAP
In Classical Frame work
0.000001 3.5 8 0.0000001

27
transient stability conditions of the equipments connected else it may be a threat to the system.
Although all the disturbances may not occur simultaneously, but they cannot be totally ignored.
Here in the simulation result of the classical framework, it may be observed that the settling
time is high, but it is measured at a very low tolerance. Again, even though the transient washout
time is more than the breaker tolerance time, it may be recalled that this breaker time is set for short
circuit condition. Now under short circuit condition the breaker should operate, which is not
protected by this stabilizer.
Table-3 (Terminal Voltage)
Type of
Model
Maximum
Overshoot
Peak Time Settling Time
Steady state
Error
RCAP in IMC Frame
work
0.0002 0.75 40 0.0001
RCAP
In Classical Frame work
-0.00018 11 40 -0.00005
B. Case-II
The performance graph of multimachine system using the following datas (Table-4) are given
bellow,
Table-4 (Generator Input data)
Fig 12: Vt ~Time in Multimachine System
From the above graph of Fig12, we got the following details,
Table-5 (Change in Delta)
MULTIMACHINE
SYSTEM
Maximum
Overshoot
Peak Time Settling Time Steady state Error
CHANGE IN ∆ 0.012% 5sec 40sec 0.0349
By changing the load at generator-1 from 0.2pu to 1pu and simultaneously at the same
change at generator-2,we have observe the variation in the change in frequency Δf1 , Δf2 and Δf1 -
Δf2 as described in figure below. Due to this change in frequency, the voltage profile at the generator
terminal gets affected. The change in frequency has been taken care of by the ALFC Loop. After
some time there will be a steady change in frequency and hence there will be a steady change in
Generator Data H=3.5;Xd=1.81;Xq=1.76;Xd’=0.3;;Xe=0.16;Rfd=0.0006;Re=0.003;
τdo’=8;KD=0;Ladu=1.65;Laqu=1;edo=0.6836;eqo=0.7298;Ido=0.8342;
iqo=0.4518;δo=79.13;Efdo=2.395;Vdo=0.72;Vqo=0.77;Vto=1
Exciters Data Lfd=0.153;Rfd=0.0006;Efdo=2.395
CPSS Data 0.003s-0.187

28
terminal voltage. This change in terminal voltage is further taken care of by the AVR and PSS in co-
ordination with each other. For the above situation the detailed characteristics of variation of rotor
angle and terminal voltage are describe in the following figure.
Fig.13: Vt ~Time in Multimachine System
Table-6 (Terminal Voltage)
Model Maximum Overshoot Peak Time Settling Time Steady state Error
Multi Machine System -2% 3.8 40 -0.000038
Fig 14: Change in Frequency at Generator-1(∆f1)
Fig 15: Change in Frequency at Generator-2(∆f2)
Fig 16: Characteristic of Change in Frequency (∆f1-∆f2)
Table-7 (Rotor Speed Deviation)
Multimachine
System
Maximum
Overshoot
Peak Time Settling Time Steady state Error
∆f1 -0.27% 2sec 40sec -0.27
∆f2 -0.28% 2.3sec 40sec -0.28
∆f1-∆f2 -2.5% 2.5 40sec -0.0003

29
REFERENCE
1. R. Behera, B.P.Panigrahi & B.B. Pati in, “Damping Control of Automatic Voltage Regulator
Loop Using Robust Control Technique”,2010 International conferences on Advances on
Recent Technologies in communication & computing, IEEE.
2. K.T.Law,D.J.Hill & N.R.Godfrey in,” Robust co-ordinated AVR-PSS Design”IEEE
transaction on power systems,Vol-9,No-3,Aug 1994
3. P.Kundur,Power System stability & control, Tata Mcgraw-Hill,Inc Newyork ,1993.
4. J.H.Chow,L.P.Harris, M.A.Kale, H.A.Othman, J.J.Sanchez.Gasca & G.E. Terwillger in,”
Robust Controller Design of power system stabilizers using multivariable Frequency Domain
Techeniques”,Proceedings of the 29th
conference on decision & control,
Honolulu,Hawaii,Dec-1990.
5. P.Kundur,M.Klein,G.J.Roger & M.S.Zywno,”Application of Power System Stabilizers for
Enhancement of overall system stability” IEEE Transaction on Power Systems,Vol PS-
4,PP.614-626,1989.
6. C.M.Lim & S.Elangovan,”Design of stabilizers in multimachine power systems”, proceeding
of IEEE,part C Vol-132,PP.146-153,May1985.
7. P.W.Sauer & M.A.Pai,Power System Dynamics & Stability, Englewood, cliffs,N J:Prentice
Hall,1998.
8. K.R Padiyar,Power System Dynamics Stability & Control,Interline publishing private Ltd
Bangalore,1996
9. K.T.Law,D.J.Hill & N.R.Godfrey in,” Robust co-ordinated AVR-PSS Design”IEEE
transaction on power systems,Vol-9,No-3,Aug 1994.
10. Ahmed A. A. Hafez, “Analysis and Design of Robust Cascaded PV System” International
Journal of Electrical Engineering & Technology (IJEET), Volume 4, Issue 5, 2013, pp. 20 -
35, ISSN Print: 0976-6545, ISSN Online: 0976-6553.
11. Archana D Wankhade and Dr. P. N. Chatur, “Robust Campus wide Network Defender”
International journal of Computer Engineering & Technology (IJCET), Volume 5, Issue 1,
2014, pp. 112 - 117, ISSN Print: 0976 – 6367, ISSN Online: 0976 – 6375.
12. Rajiv Ranjan and Dr. Pankaj Rai, “Robust Model Reference Adaptive Control for A Second
Order System” International Journal of Electrical Engineering & Technology (IJEET),
Volume 4, Issue 1, 2013, pp. 9 - 18, ISSN Print: 0976-6545, ISSN Online: 0976-6553.

Multi-machine stability study using robust AVR-PSS

Recommended

Recommended

More Related Content

What's hot

What's hot (18)

Viewers also liked

Viewers also liked (20)

Similar to Multi-machine stability study using robust AVR-PSS

Similar to Multi-machine stability study using robust AVR-PSS (20)

More from IAEME Publication

More from IAEME Publication (20)

Recently uploaded

Recently uploaded (20)

Multi-machine stability study using robust AVR-PSS