Квадратична функція

1. Алгебра 9

3. Як називається
графік функції
?
2
ху 

4. Від чого залежить
напрямок віток
параболи
?
2
аху 
а > 0
а < 0

5.  2
4 ху
42
 ху

6.  2
5 ху
52
 ху

7. 22
 ху
22
 ху

8.  2
1 ху
12
 ху

9.   12
2
 ху
  12
2
 ху

10.   15
2
 ху

11.   23
2
 ху

12.   63
2
 ху

13. х
у
10
6
-3
3
  33
2
 ху
Вершина  3;3 
- парабола, вітки вгору
1х 2х
Нулі функції: ;0у
  ;033
2
х
  ;33
2
х
;33 х
;332,1 х
Точки перетину з віссю ОУ:
;0х   .639330
2
у
•
•
•
•
у
у
•
П
П
•
Властиво
сті

14. х
у
10-3
хх 243 
3 ху
ху 24
х у
0 2
4 0
ху  На 3 од
←
- пряма
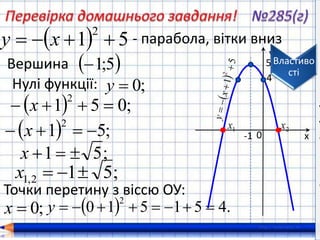
1х

15. 4
  .451510
2
у
х
у
-1 0
5
  51
2
 ху
Вершина  5;1
- парабола, вітки вниз
1х 2х
Нулі функції: ;0у
  ;051
2
 х
  ;51
2
 х
;51 х
;512,1 х
Точки перетину з віссю ОУ:
;0х
•
•
•
•
у
у
•
П
П
•
Властиво
сті

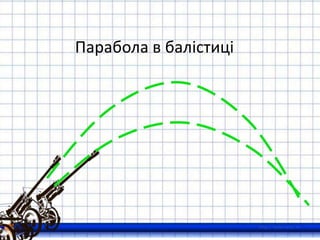
17. «Судьба, как ракета, летит по
параболе
Обычно – во мраке и реже –
по радуге. …»
«…Сметая каноны, прогнозы,
параграфы,
Несутся искусство, любовь и
история –
По параболической
траектории!»

18. Алгебра 9

19. Траєкторія м’яча
Рух тіла, кинутого під кутом до
горизонту

20. Стрибки вгору

21. Стрибки в довжину

22. Парабола в балістиці

23. Рух по параболі

24. Параболічна орбіта супутника

25. Параболічна орбіта супутника
Якщо космічному кораблю чи штучному супутнику, який
обертається навколо Землі, надати другу космічну
швидкість, то його траєкторія руху перетвориться з
еліптичної в параболічну, і він зможе покинути Землю.

26. cbxаху  2
Квадратична функція
Квадратичною називають функцію,
яку можна задати формулою виду
де - незалежна змінна, і - деякі
числа, до того ж
x bа, с
.0а
Наприклад: 322
 xху
xху 22
 55,0 2
 xху
42
 ху
2
7
2
ху 
2
4 ху 

27. Формула координати тіла:
Рівноприскорений рух
2
00
2
1
attvхх 
2
0
2
1
attvS 
Формула шляху:
Довідка

28. Графік квадратичної функції
Квадратична функція:
Функція виду:
cbxаху  2
  nmхау 
2
 nm;
парабола з вершиною:

29. «Виділення повного квадрату»

31. Побудуй графік
квадратичної функції:
662
 xху
а
b
с
 ,;nm ,
2a
b
xm в 
 .nууn в 

32. 3
12
6



 вxm
Побудуй графік
квадратичної функції:
662
 xху
1а
6b
6с
 3;3   33  ууn в

33. Побудова графіка
cbxаху  2
квадратична-
1. Напрямок віток параболи.
,
2a
b
т

2. Вершина параболи: .
 myn 
 nт;
- вісь симетрії.
,0у ;02
 cbxах
3. Нулі функції. Точки перетину з осями
функція, графік – парабола.
,0х   .0 суу 

34. Побудуй графік
квадратичної функції:
422
 xху
а
b
с
 nm;
a
b
xm в
2

 nууn в 

35. Побудуй графік
квадратичної функції:
422
 xху
1а
2b
4с
 5;1
 
1
12
2



 вxm
  51  ууn в

36. хо
у
1 2 3 4 5
1
2
3
4
5
-1
-2
-3
-4
-5
-1-2-4-5-6 -3
• Планета рухається
навколо сонця по
колу радіуса 5
астрономічних
одиниць;
• траєкторія комети
описується законом
у = 1/4х² - 1.
• Чи перетинається
траєкторія комети з
орбітою планети?

37. Траєкторія струменю води

39. Опрацювати п.12, №322.
Побудувати графіки. Вивчити алгоритм
побудови графіка квадратичної функції.