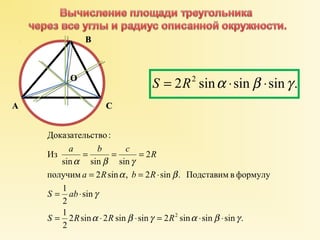
Документ содержит формулы для вычисления площадей различных треугольников, включая формулу Герона и методы, связанные с координатами. Обсуждаются формулы, вытекающие из теоремы косинусов, а также формулы для определения радиусов вписанных и описанных окружностей. В документе также рассматриваются вычисления для конкретных примеров треугольников с заданными сторонами и координатами.

1. Формулы для вычисления площадей
различных треугольников
.

2. ВВ СС
АА
DD
bb
aa

3. 1
S = a × ha
2
1
1
S S S CD h DB h
= + = × + × =
ABC ADC ADB a a
CD DB h СB h 1
a h
( ) 1
2
= + = × = ×
a a a
2
2
1
2
2

4. sing
S =1 ab ×
2
A
ɣ
c
hа
b
С B
a D
1
треугольника ADC h sin , 1
g sing
2
, но из прямоугольного
2
a = × = ×
= ×
b S ab
S a h
ABC
ABC a

5. АА
BB
CC
OO
.
rr
S S S S AB r ABC BOC AOB AOC
1
1
AC r BC r a b c r
+ × + × = + + ×
( )
2
1
2
1
2
2
r =
радиус вписанной окружности
= + + = × +

6. AA
BB
= × ×
OO R
CC
S a b c
4
abc
R
знаем, что S 1
ABC
= = = =
R abc
R
Мы ab C
, S 1
2 2 4
2 ; sin C c
2R
с
sin C
sin ; sin C найдем из соотношения
2
ABC
= ×
RR

7. BB
сс
aa
AA CC
bb
S = p( p - a)( p - b)( p - c)

8. Доказательство: По теореме косинусов можно записать:
2 2 2
= + - ×
c a b 2ab cosγ
2 2 2
× = + -
2ab cosγ a b c ,
2 2 2
= + -
cosγ a b c
÷ ö
æ + ÷ø
+ - 2 2 2 2 2 2
sin γ 1 cos γ (1 cos )(1 cos ) 1 a b c
= - - + × 2ab + a + b - c
= c - (a - b)
× + - =
2 2
2ab a b c
(c a b)(c a b)(a b c)(a b c).
1
4a b
1 a b c
(a b) c
2ab
2ab
2ab
2ab
2ab
2ab
.
2ab
2 2
2 2 2 2 2 2 2 2 2 2
= - + + - + - + +
ö
= ÷ ÷ø
ç çè
ç çè æ + - = - = - + = -
g g
Т.К.
a + b + c =
p
a + b - c = a + b + c - 2 c = 2 p -
2
c
c + a - b = c + a + b - 2 b = 2 p -
2
b
2 2 2 ,
2
c - a + b = c + b + a - a = p -
a
то
(2p 2a)(2p 2b)(2p 2c) 2p 16
sin 1
g = × - - - × = - - - × =
= - - - ×
(p a)(p b)(p c) p.
= × - - -
p(p a)(p b)(p c) p(p a)(p b)(p c).
4
sinγ 2
ab 2
2
ab
S. 1
p (p a)(p b)(p c).
ab
a b
(p a)(p b)(p c) p
4a b
4a b
2 2
2 2 2 2
2
= × - - - = - - -
ч.т.д.

9. ГЕРОН АЛЕКСАНДРИЙСКИЙ
(Heronus Alexandrinus)
Герон Александрийский – греческий учёный,
работавший в Александрии,(даты рождения и смерти
неизвестны, вероятно, I – II вв. н. э. ).
Математические работы Герона являются
энциклопедией античной прикладной математики. В
"Метрике" даны правила и формулы для точного и
приближённого расчёта различных геометрических
фигур, например формула Герона для определения
площади треугольника по трём сторонам, правила
численного решения квадратных уравнений и
приближённого извлечения квадратных и кубических
корней. В основном изложение в математических
трудах Герона догматично – правила часто не
выводятся, а только выясняются на примерах.
Герон занимался геометрией, механикой,
гидростатикой, оптикой.

10. a
b
c
S = 1 ab - a + b - c
4 ( )2
4
p = a + b + c
2
ö
æ
b a b c
æ
ö
æ
= + + + + -
b c b c a a b c a b c
= + + + - - + + - =
b c a b c a a b c a b c
= + - + - - - + - =
b c a a b c b bc c a a b bc c
= + - - - = + + - - + - =
2
a a b c
a b c
S a b c
(( ) 2 )( ( ) 2
1
4bc (b c a)
(2 ( ))(2 ( )) 1
4
1
1
1
1
4
( 2 )( 2 )
4
4
(( ) )(( ) )( ( ))( ( ))
4
( a )( )( )( )
4
c
2
2
2
2
= + + - - + - = - + -
ö
= ÷ ÷ø
ç çè
+ + -
÷ ÷ø
ç çè
+ + -
÷ ÷ø
ç çè
bc b c a bc b c a
BB
AA CC

11. Итак, мы получили II формулу Герона. И если стороны
треугольника а,b,с , то запишем ее в виде:
S = 1 a b - a + b - c
4 2 2 ( 2 2 2 )2
4
CC
cc
BB
bb
aa
AA

12. Найти площадь треугольника со сторонами 17 20 13
17
S = 1 a b - a + b - c
4 2 2 ( 2 2 2 )2
4
1 2 S = × × - + - = - = =
1040 256 1
4
784 7
4
4 13 20 (13 20 17) 1
4
20
13
, ,

13. Формулы медиан треугольника
2 2 2
а
2
AADD-- ммееддииааннаа..
2 2 2
2 2 2
2 2
m a c b
1
2
= + -
2 2
1
2
2 2
1
2
m a b c
m b c a
c
b
a
= + -
= + -
Из треугольника ACD по теореме косинусов:
cosγ a
2
= + - × × = + - ×
a 4b 4m
b m
m b a
a
Из треугольника АВС по теореме косинусов:
2 2 2
= + - ×
с a b 2ab cosγ
2 2 2
= + -
cosγ a b c
Приравнивая формулы (1) и (2) получаем:
a b c a
+ - = + -
= + - - +
2b a b c
2m a
2m b a
= - +
m 1
2 = 2 + 2 -
2
a
(2b 2c a )
4
2 2 2
m 1
a
2
2
2 2
a
2 2 2 2
2
2
a
2
a
2
2
2 2 2
2
a
2 2
2
a
2
2
2
2 2
2
a
2b 2c a
2
c
2
2
2b 2m
2
(2)
2ab
(1)
4ab
ab
4
cosγ
b ab cosγ
4
2b a
4
= + -
= + -
+ -
=
BB
АА CC
bb
aa
cc
DD
а m
g

14. hc
По второй формуле Герона:
2 2 2 2 2 2
) S ( ) ( ) (( ) ( ) ( ) )
= × × - + - =
196 14
2
10
1
5 2
520 324 1
Проведем высоту СК h ,
7
= + -
10 5 13
2 5 2
1 1
4 10 13 ( 10 13 5 )
1
2)
= = × =
h S
2 2 3 5
2 2 2
) B = a + c -
b
2
B = ( ) + ( ) -
( )
1
cos 10 5 13
2 10 5
3 cos
2 2 2
= =
×
× ×
,
ac
5 26
14
= × × = × ×
5 10 13
4 =
S ,
4 3 5
4
×
) R a b c
Дано треугольник
: ABC
=
с 5
10
13
а
в
=
=
Найти
S
1) .
ABC
h
2) .
:
c
3) cos B.
4) R( радиус описанной окружности).
26 10 10 26
2
7
2 ( 13) 2 ( 5) ( 10) 1
2
=
5) Проведем медиану AD m
2b 2c a , m 1
2
m 1
2
2 2 2
a
2 2 2
a
a
= + - = × + × - = + - =
5) Медиану AD
3,5
2
4
4
4
4
4 10 13 10 13 5
4
2
× × - + - = - = = = =
5
5
=
; h ,
с
c c
c
C
13
D
10
A 5 B

15. Найти площадь треугольника АВС если, А(0;6) B(4;-2) C( 2;18)
Из построения видно, что треугольник АВС разносторонний, и ни одна из высот не
параллельна оси координат.
2 2
= - + - - =
AB (4 0) ( 2 6) 80
2 2
= - + + =
BC (2 4) (18 2) 404
2 2
= - + - = + =
AC (2 0) (18 6) 4 144 148
Найдем площадь треугольника по II формуле Герона..
66 S = 1 4 × 80 × 404 - (80 + 404 - 148) 2
= 1
- =
16384 1
4
128 32
4
Как мы видим здесь очень громоздкие вычисления и без
калькулятора не обойтись. Тогда встает вопрос . А нет ли
какой-нибудь формулы попроще, чтоб посчитать площадь
треугольника в прямоугольной системе координат? И вот
эта формула.
1
129280 112896
4
4
= = × =
00
-22
44
1188
y
xx

16. Пусть вершины треугольника АВС имеют следующие координаты:
А( х1; у1), В (х2; у2), С( х3; у3)
Применим эту формулу к нашему примеру.
4-0 2-0 4 2
S = ½ = ½ = ½ (48+ 16)= 32.
-2-6 18-6 -8 12
1
у - у у - у
Если предположить, что х1=у1=0, то получится еще более простая формула:
Вывод этой последней формулы приводится ниже .
2 1 3 1
2 1 3 1
2
х - х х х
S
-
=
( ) 3 3 с х у
( ) 2 2 В х у
''(0; ) 3 С у
''( ; ) 2 В O у
''(0; ) 1 А у
( ; ) 1 1 А х у
( ) 2 1 у - у
'( ;0) 1 А х '( ;0) 3 с х '( ;0) 2 В х
( ) 2 1 х - х
( ) 3 1 х - х
XX
YY
1
S = 1 x y - x y
2 3 3 2 2
( )( ) ( )( )
2
2 1 3 1 3 1 2 1 S = x - x y - y - x - x y - y

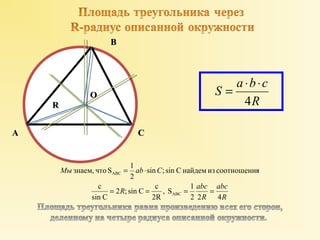
17. Пусть требуется найти площадь S треугольника АВС с вершинами А (х1; у1), В( х2; у2), С( х3; у3).
Пусть АВ= с, АС = b, а углы, образованные этими сторонами осью Ох, соответственно равны α и β
А' B' = cx= c cos α= x2-x1 (1)
A’’B’’= cy= c sin α = y2-y1
А' C' = bx= b cos B= x3-x1 (2)
A’’C’’= by= b sin B = y3-y1
Прямоугольная система координат на плоскости:
Пусть ф = угол САВ; очевидно
ф = β – α
По известной формуле тригонометрии получаем:
S= ½ bc sin ф = ½ bc sin (β – α) = ½ bc(sin β cos α- cosβ sinα ) = ½(by cx- bx cy) (3)
Отсюда в силу (1) (2) имеем:
S= ½ [(y3-y1) (x2-x1) – (x3-x1) (y2-y1)] (4)
Заметим, что формула (4) при ином расположении вершин может дать площадь треугольника S со знаком минус.
Поэтому формулу для площади треугольника обычно пишут в виде:
S= +/- ½ [(x2-x1) (y3-y1) – (x3-x1) (y2-y1)] (4’)
Где знак выбирается так, чтобы для площади получалось положительное число.
Формулу (4) можно записать в удобном для запоминания форме:
х2-х1 х3-х1
S= ½
у2-у1 у3-у1

18. Восемь формул для нахождения
площадей различных треугольников.
= 1
S ab
1
S = 1 ab ×
х - х у
-
у
1 0 1 0
2 0 2 0
1
2
у - у
х х
S
-
=
2
S = a × ha
2
S = 1 a b - a + b - c
S = (a + b + c)× r 2
sing
2
S = p( p - a)( p - b)( p - c)
4 2 2 ( 2 2 2 )2
4
1
S = a × b ×
c
R
4

19. С
а
в
α β
с
Ɣ
А В
2 sin sin
S c α β
= ×
a b
sin sin
2sin( )
S c α β
(α +
β)
= ×
= ° - +
Из a b c a c b c
= ×
2sin
(α β)
= × = × × × = × × = ×
+
a b
sin sin
b
2sin(180 ( ))
, sin
следует sin
a
g a b
sin sin sin
2sin
sin
sin
g a b
g sin
a
sin
sin sin
Доказательство :
180 ( )
sin 1
2
1
2
sin
sin
sin sin sin
(1)
2sin
2 2 2
2
a b
a b
g
b
g
g
g
g
a b g
+
° - +
= = = × = ×
S ab c c c c c

20. Ɣ
α β
А
С
В
а
с
в
Доказательство :
a b a b a b
+ = × + × =
Т.к. sin( ) sin cos cos sin
S c
sin sin ( ).
a
cos
sin
= a × b æ b
+
sin sin cos
sin
ö
Подставляя в формулу (1), получим:
2 2
= × ×
a b
sin sin
c
a b a b a b
.
S c
2( )
.
2sin sin ( ) 2( )
2
a b
a b a b
a
b
ctg ctg
ctg ctg
ctg ctg
S c
ctg ctg
+
=
+
=
× +
+ × = ÷ ÷ø
ç çè
.
2
ctga +
ctgb
2( )
=

21. S = 2R2 sina ×sinb ×sing .
a b c 2
R
Доказательство :
= = =
a b g
sin sin sin
a R b R
= = ×
a b
получим 2 sin , 2 sin . Подставим в формулу
1
S ab
= ×
2
1
sin
g
S R R R
2 sin 2 sin sin 2 sin sin sin .
2
Из
a b g 2 a b g
= × × = × ×
AA
BB
CC
OO

22. S = a2 sin ×sin
b g
2sin
a
A
Ɣ
а
в
a b c b a
S ab S a a a
g sin b sin
g
sin
sin 1
2
= = = ×
g sin
b
sin
имеем sin
sin ; 1
2
Доказательство :
Подставим в формулу 1
2
sin
sin sin sin
Из
2
a
a
b
a b g
= × = × × × = ×
С
α β
А В

23. Вычисление площади треугольника через радиусы
вневписанных окружностей.
Oa
Ob
Oc
β
a
Ɣ b
c
α
Вневписанная окружность- это
окружность, касающаяся одной
стороны треугольника и продолжения
двух других сторон.
S = r p - a = r p - b = r p -
c
( ) ( ) ( )
a b c
S = r × r × r ×
r
a b c
r , r ,
r радиусывневписанных окружностей
a b c
p -
полупериметр
-
с r
b r
а r

24. Интернет-ресурсы
• Сайт http://www.webmath.ru
• Вычисление площади треугольника
• Формула площади треугольника, онлайн
сервис для расчета площади
треугольника. Нахождение площади
треугольника 7-ю методами, всего за
несколько секунд Вы найдете площадь
треугольника.