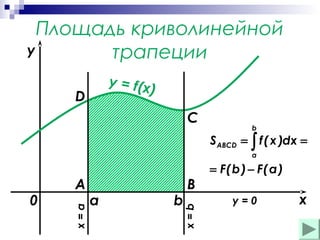
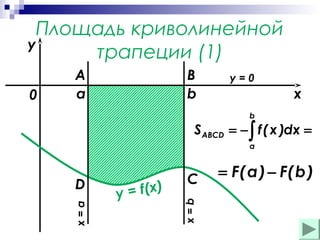
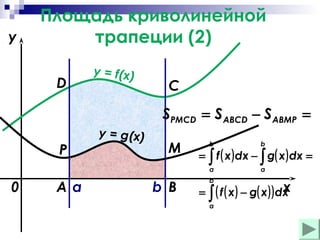
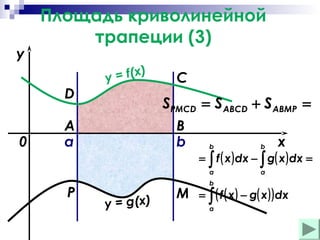
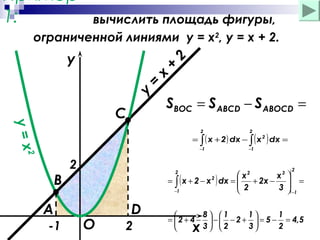
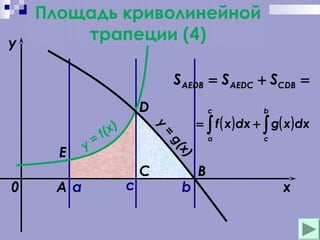
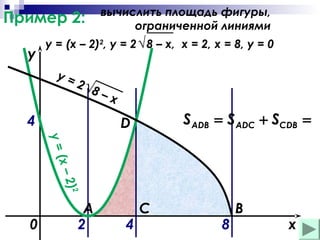
Документ обсуждает основные понятия первообразной и неопределенного интеграла, включая формулы, примеры и правила нахождения первообразных. Он также охватывает методы вычисления площади криволинейных фигур. Приводятся примеры расчетов площадей, ограниченных графиками функций.

1. Первообразная
Интеграл

2. Содержание

Понятие первообразной

Неопределенный интеграл

Таблица первообразных

Три правила нахождения первообразных

Площадь криволинейной трапеции

Площадь криволинейной трапеции (1)

Площадь криволинейной трапеции (2)

Площадь криволинейной трапеции (3)

Площадь криволинейной трапеции (4)

Пример (1)

Пример (2)

3. Понятие первообразной
Функцию F(x) называют первообразной для
функции f(x) на интервале (a; b), если на нем
производная функции F(x) равна f(x):
F ′( x ) = f ( x )
Операцию, обратную дифференцированию
называют интегрированием.

4. Примеры
1. f(x) = 2x; F(x) = x2
F′(x)= (x2)′ = 2x = f(x)
2. f(x) = – sin x; F(x) = сos x
F′(x)= (cos x)′ = – sin x = f(x)
3. f(x) = 6x2 + 4; F(x) = 2x3 + 4x
F′(x)= (2x3 + 4x)′ = 6x2 + 4 = f(x)
4. f(x) = 1/cos2 x; F(x) = tg x
F′(x)= (tg x)′ = 1/cos2 x= f(x)

5. Неопределенный интеграл
Неопределенным интегралом от непрерывной
на интервале (a; b) функции f(x) называют
любую ее первообразную функцию.
f ( x )dx = F ( x ) + c
∫
Где С – произвольная постоянная (const).

6. Примеры
′=A
1. ∫ Adx = Ax + C ; ( Ax + C )
2. ∫ e dx = e + С ;
x
x
(e
x
4. ∫ x dx =
+ С;
4
3
)
′
+C =e
x
( − cos x + C)
3. ∫ sin xdx = − cos x + С ;
4
x
′
′=
( tg x + C )
1
2
cos x
= sin x
′
x
 1
 + С  = ⋅ 4x 3 = x 3
 4

4


1
5. ∫
dx = tg x + C ;
2
cos x
4

7. Три правила нахождения
первообразных
1º Если F(x) есть первообразная для f(x), а G(x) –
первообразная для g(x), то F(x) + G(x) есть
первообразная для f(x) + g(x).
2º Если F(x) есть первообразная для f(x), а k –
постоянная, то функция kF(x) есть первообразная
для kf.
3º Если F(x) есть первообразная для f(x), а k и b –
1
постоянные, причем k ≠ 0, то функция k F(kx + b)
есть первообразная для f(kx + b).

9. Площадь криволинейной
y
трапеции
y = f(x
D
)
C
b
S ABCD = ∫ f ( x )dx =
a
a
b
B
x=b
x=a
0
A
= F( b ) − F( a )
y=0
x

10. Площадь криволинейной
y
трапеции (1)
B
b
y=0
x
b
S ABCD = − ∫ f ( x )dx =
a
= f(x)
y
C
x=b
D
x=a
0
A
a
= F( a ) − F( b )

11. y
Площадь криволинейной
трапеции (2)
D
y = f(x)
y = g(x)
C
SPMCD = S ABCD − S ABMP =
M
0
Aa
b B
b
a
P
b
a
= ∫ f ( x ) dx − ∫ g( x ) dx =
b
=
x
( f ( x ) − g( x ) ) dx
∫
a

12. y
Площадь криволинейной
трапеции (3)
D
0
= f(x)
y
C
SPMCD = S ABCD + S ABMP =
A
a
B
b
b
a
P
b
a
= ∫ f ( x ) dx − ∫ g( x ) dx =
b
y = g (x )
x
M = ∫ ( f ( x ) − g( x ) ) dx
a

13. Пример
1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
y
y=x
C
=
x
+
2
SВОС = S ABCD − S ABOCD =
2
2
−1
−1
( )
= ∫ ( x + 2) dx − ∫ x 2 dx =
2
B
A
-1
2
2
=

( х + 2 − х ) dx =  x2
∫

2

−1
O
D
2
2
+ 2x −
3
x
3
2

 =

 −1
8 1
1
1

=  2 + 4 −  −  − 2 +  = 5 − = 4,5
3  2
3
2

x

14. y
Площадь криволинейной
трапеции (4)
S АЕDВ = S AEDC + SСDB =
D
a
x
g(
с
)
Aa
=
0
b
= ∫ f ( x ) dx + ∫ g( x ) dx
y
Е
y=
x)
f(
с
с
C
b
B
x

15. вычислить площадь фигуры,
ограниченной линиями
Пример 2:
y
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y=
2√
8–
4
x
S АDВ = S ADС + SСDB =
D
y=
(x –
2
2)
0
A
2
4
C
8
B
x

16. вычислить площадь фигуры,
ограниченной линиями
Пример 2:
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
=
∫ ( x - 2)
2
2
8
dx + ∫ 2
4
( x − 2)
8 - хdx =
3
3 4
2
4( 8 − x ) 8 − x
−
3
8
=
4
 ( 4 − 2) 3 ( 2 − 2) 3   4( 8 − 8 ) 8 − 8 4( 8 − 4 ) 8 − 4 
−
=
=
−
−

 3
3  
3
3


 
8 32 40
1
= +
=
= 13
3 3
3
3