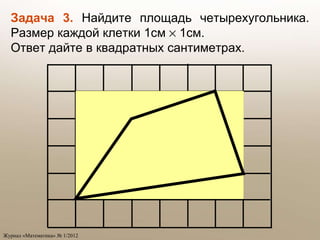
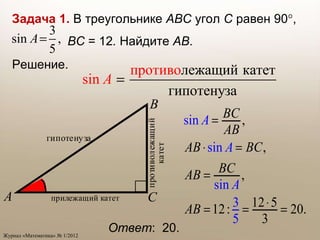
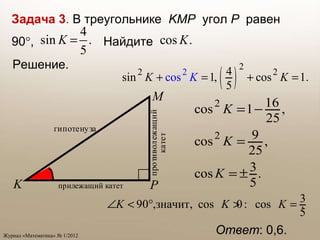
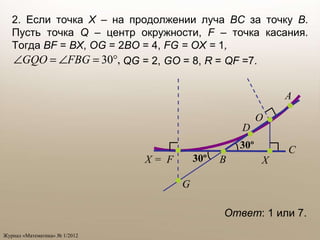
Документ содержит задачи по геометрии и тригонометрии, направленные на нахождение площадей плоских фигур и значений тригонометрических функций. Задачи включают нахождение площадей треугольников и четырехугольников, а также использование формул для решения угловых проблем в треугольниках. Также рассматриваются операции с координатами и векторами, связанных с приложением теоремы Пифагора и теоремы синусов.

1. Е. Зудина г. Москва ГЕОМЕТРИЯ

2. Задача В3 Задача В6 Задачи на нахождение площадей плоских фигур, нарисованных на клетчатой бумаге или расположенных на координатной плоскости. Задачи на нахождение значений тригонометрических функций углов по известным элементам геометрических фигур и, наоборот, нахождение неизвестных элементов геометрических фигур по известным значениям тригонометрических функций.

3. Проверяемые умения Для решения требуется Задача В3 Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Знать формулы площадей треугольников, параллелограммов, трапеций, круга и его частей. Применять указанные формулы для нахождения площадей фигур, находить площадь фигуры методом разбиения ее на более простые фигуры.

4. a a b b

5. Задача 1. Найдите площадь треугольника. Размер каждой клетки 1см  1см. Ответ дайте в квадратных сантиметрах.

6. Решение. 1. Построим прямоугольник, в вершинах и на сторонах которого лежат вершины данного треугольника.

7. 2. Закрасим «лишние» треугольники.

8. Ответ : 12. 3. Вычислим площади прямоугольника и «лишних» треугольников. 4. Вычислим площадь данного треугольника.

9. Задача 2. Найдите площадь четырехугольника. Размер каждой клетки 1см  1см. Ответ дайте в квадратных сантиметрах.

10. Ответ : 12. Решение.

11. Задача 3. Найдите площадь четырехугольника. Размер каждой клетки 1см  1см. Ответ дайте в квадратных сантиметрах.

12. Ответ : 13. Решение.

13. Задача В6 Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Знать определения тригонометрических функций и их свойства. Уметь работать с формулами, выполнять арифметические действия и преобразования числовых выражений. Для решения требуется Проверяемые умения

15. Ответ : 20. Задача 1. В треугольнике АВС угол С равен 90  , ВС = 12 . Найдите АВ . Решение.

16. Задача 2. В треугольнике ВСН угол Н равен 90  , ВН = 24. Найдите СН . Ответ : 10. Решение.

17. Задача 3 . В треугольнике KMP угол P равен 90  , Найдите Ответ : 0,6. Решение.

18. Ответ : 0,6. Задача 4. В треугольнике ABC AC = BC , AB = 10, высота AH равна 8. Найдите cos A . В прямоугольном треугольнике ABH катет BH находим по теореме Пифагора: , откуда cos B = 0,6. Так как углы A и B треугольника ABC равны, то cos A = 0,6. Решение.

19. Задача 5. Найдите хорду, на которую опирается угол 60 ° , вписанный в окружность радиуса . Рассмотрим треугольник ABC : – теорема синусов. Ответ : 3. Откуда Решение.

20. Задача С4 Задачи на нахождение значений тригонометрических функций углов по известным элементам геометрических фигур и, наоборот, нахождение неизвестных элементов геометрических фигур по известным значениям тригонометрических функций.

21. Задача 1. На стороне BA угла ABC , равного 30°, взята такая точка D , что АD = 2 и BD = 1. Найдите радиус окружности, проходящей через точки A , D и касающейся прямой BC . Пусть окружность и прямая ВС касаются в точке Х. Тогда т.е. Если точка Х лежит на луче ВС , то центр окружности – точка О – середина отрезка AD : Решение. D B A C O X = E

22. Ответ : 1 или 7. 2. Если точка X – на продолжении луча BC за точку B . Пусть точка Q – центр окружности, F – точка касания. Тогда BF = BX , OG = 2 BO = 4, FG = OX = 1 , QG = 2 , GO = 8, R = QF =7. D B A C O X = F X G