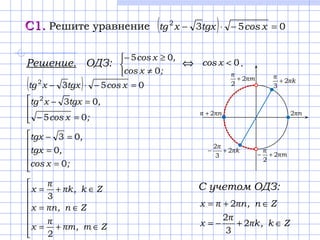
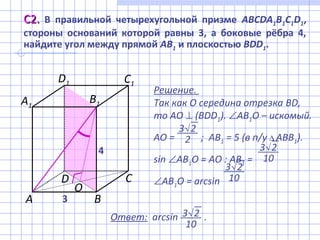
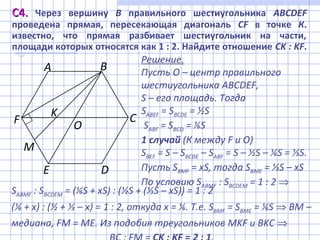
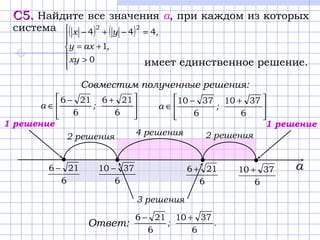
Документ содержит решения задач по математике, относящихся к экзамену ЕГЭ, включая уравнения, неравенства и геометрические задачи. В нем представлены подробные вычисления и объяснения, которые позволяют найти угол в призме, решить неравенства и определить условия для уникальности решений системы уравнений. Также рассматриваются вопросы анализа натуральных чисел и их свойств в наборе.