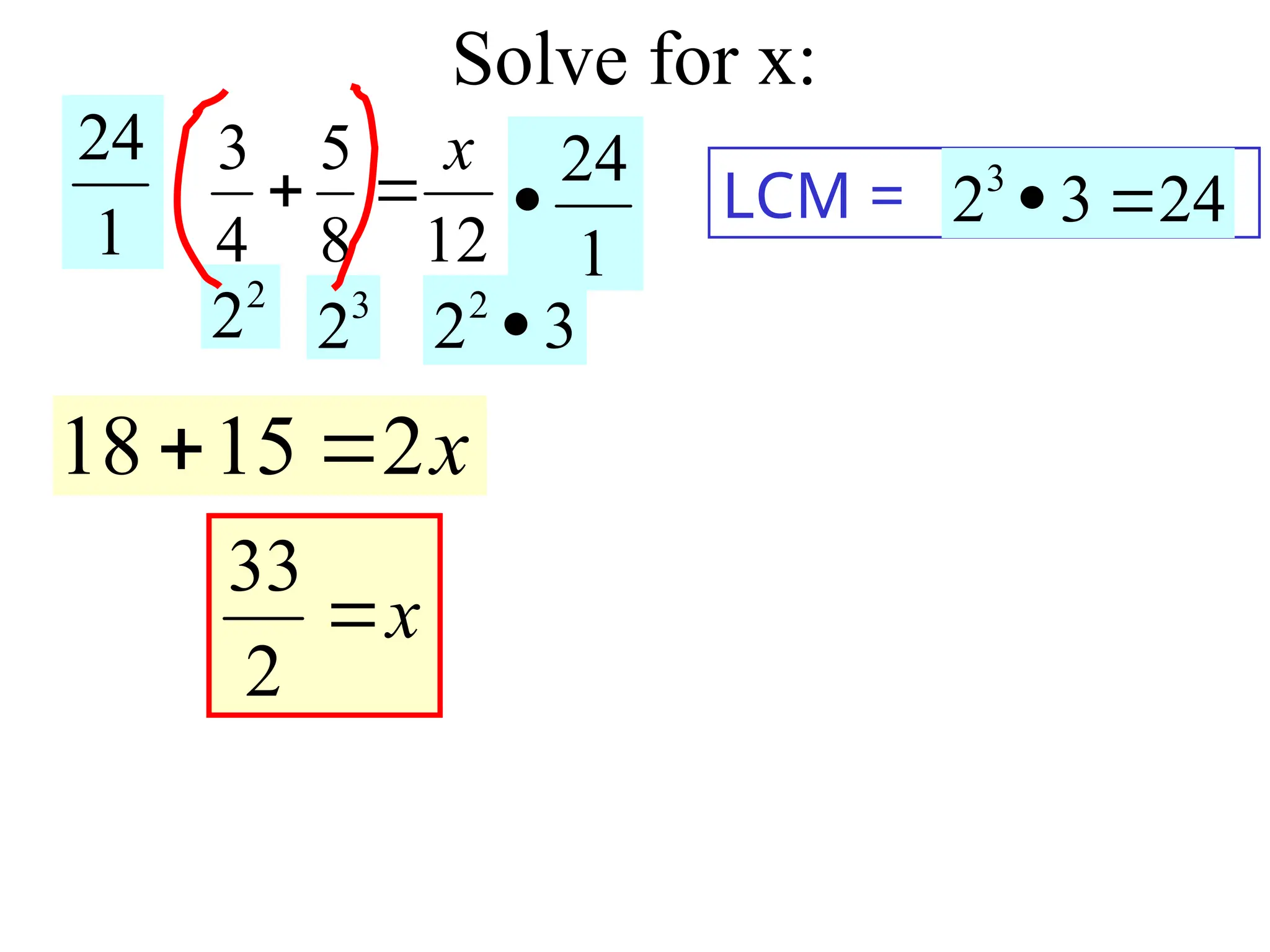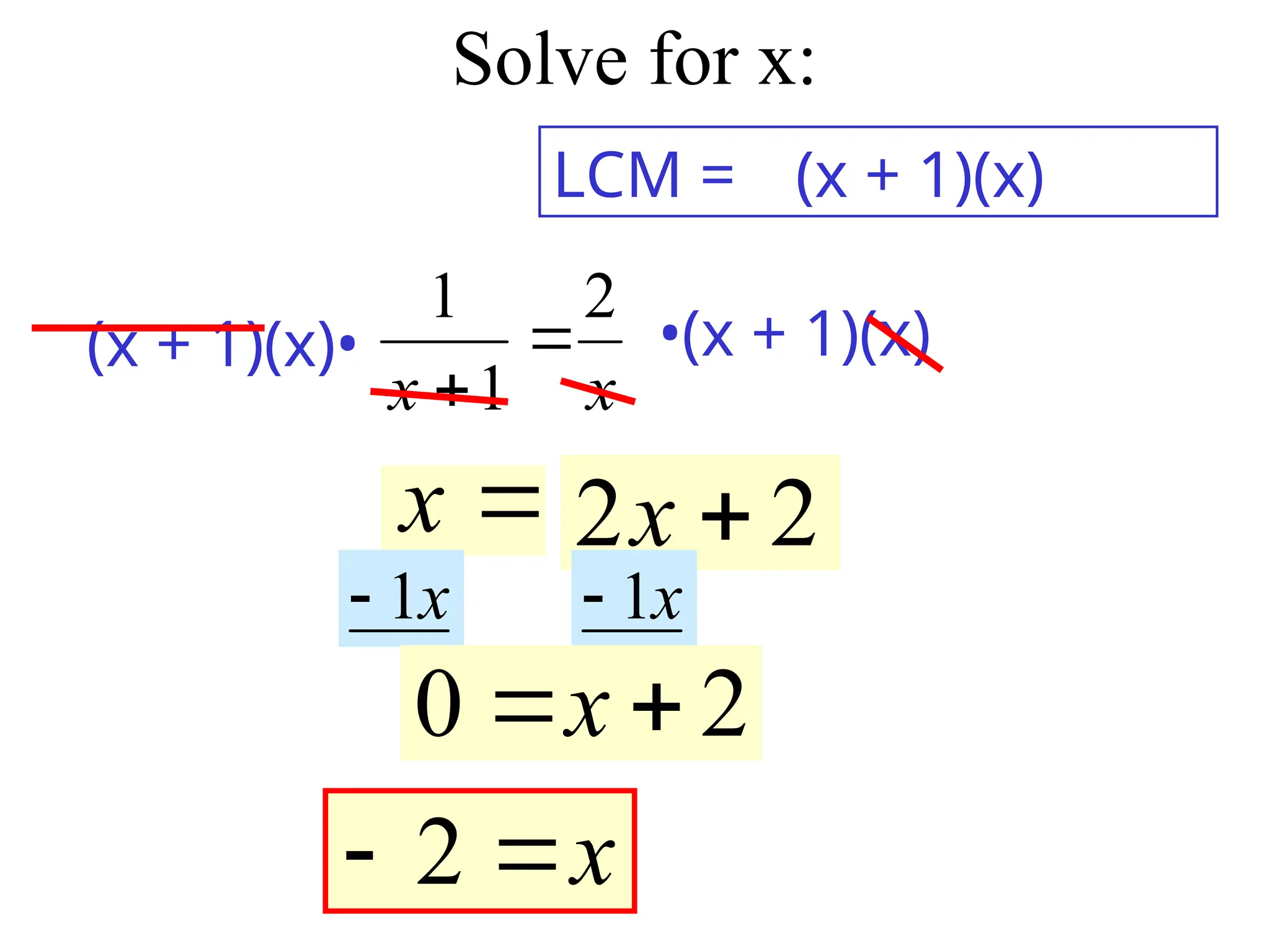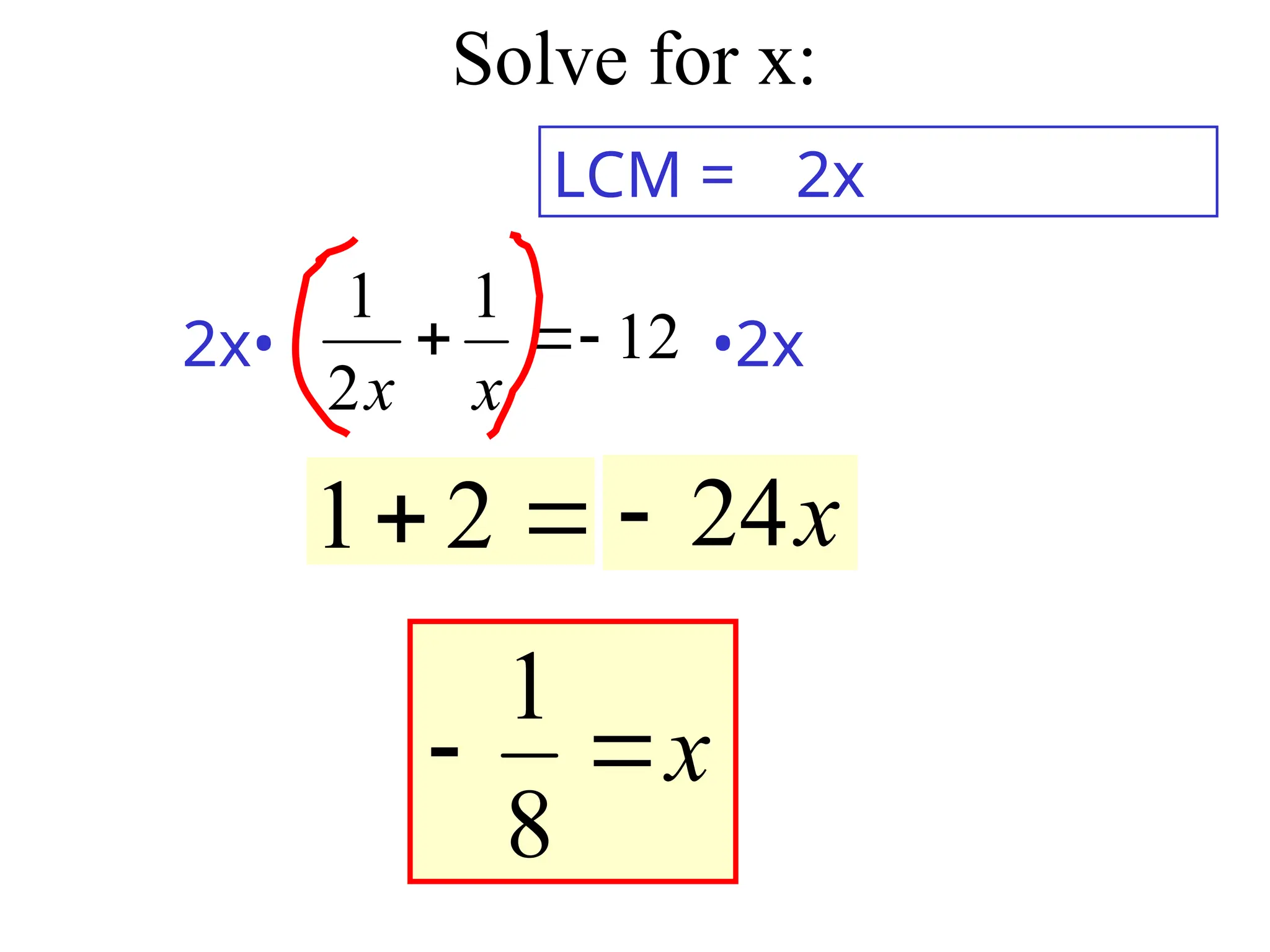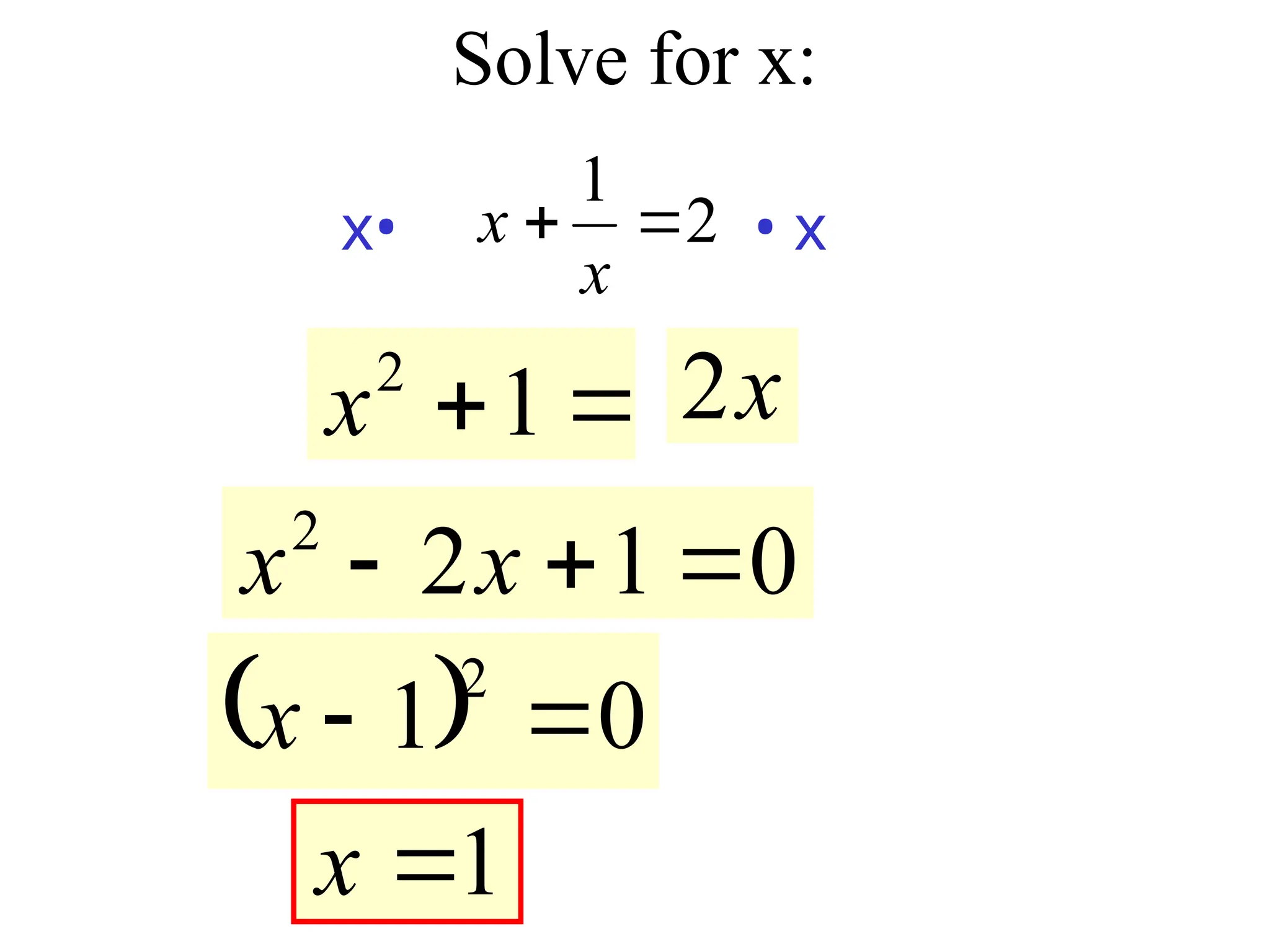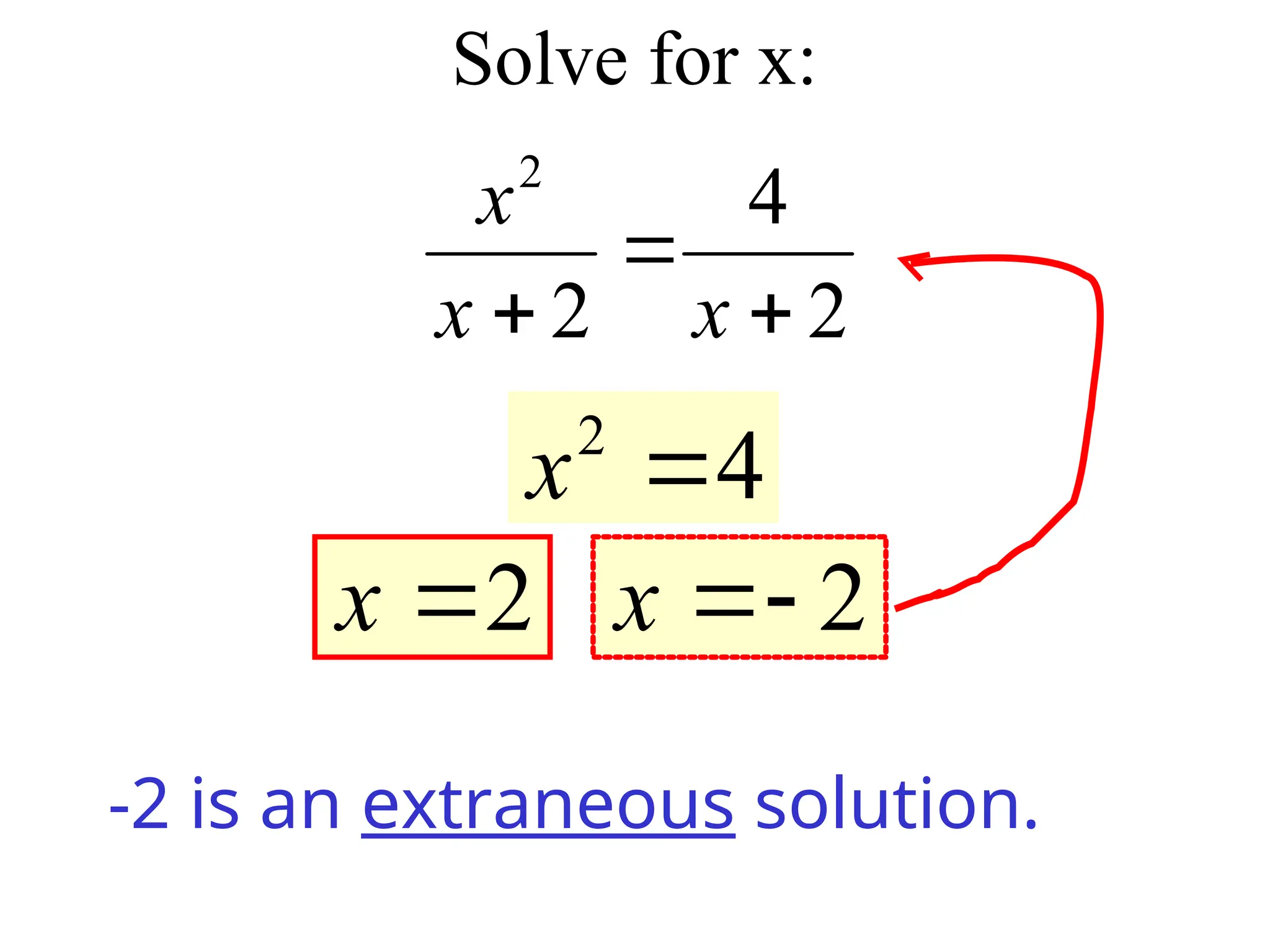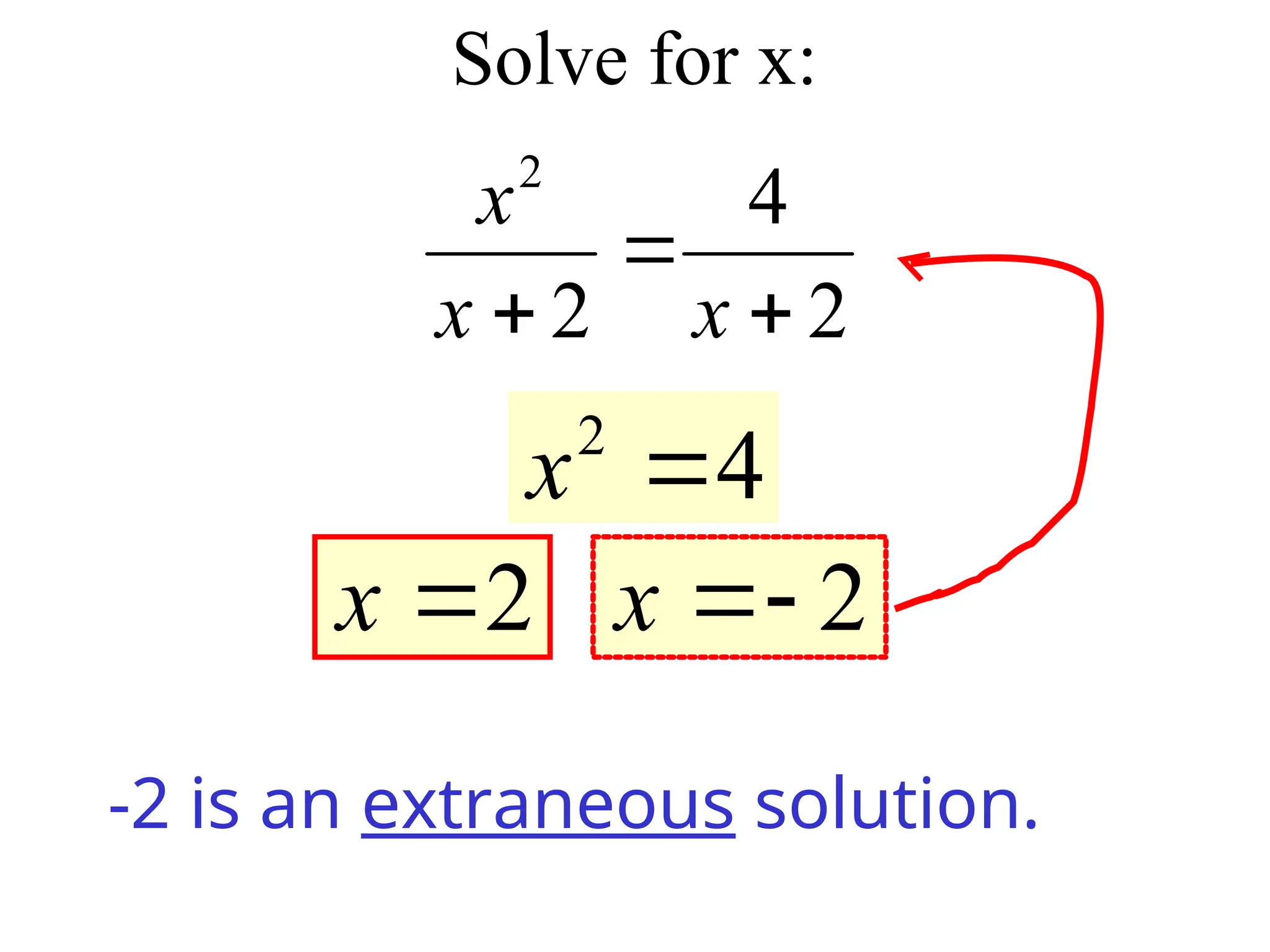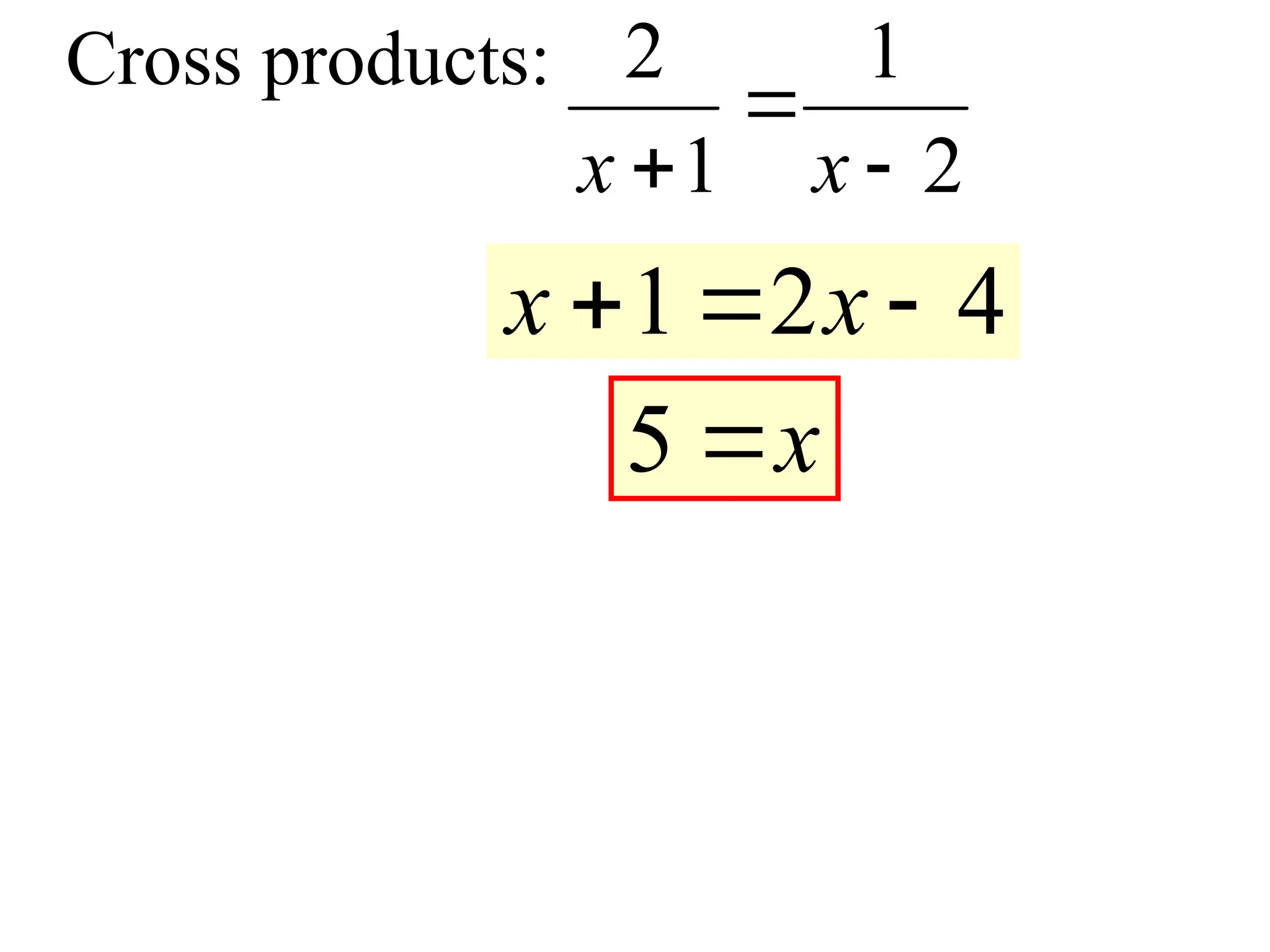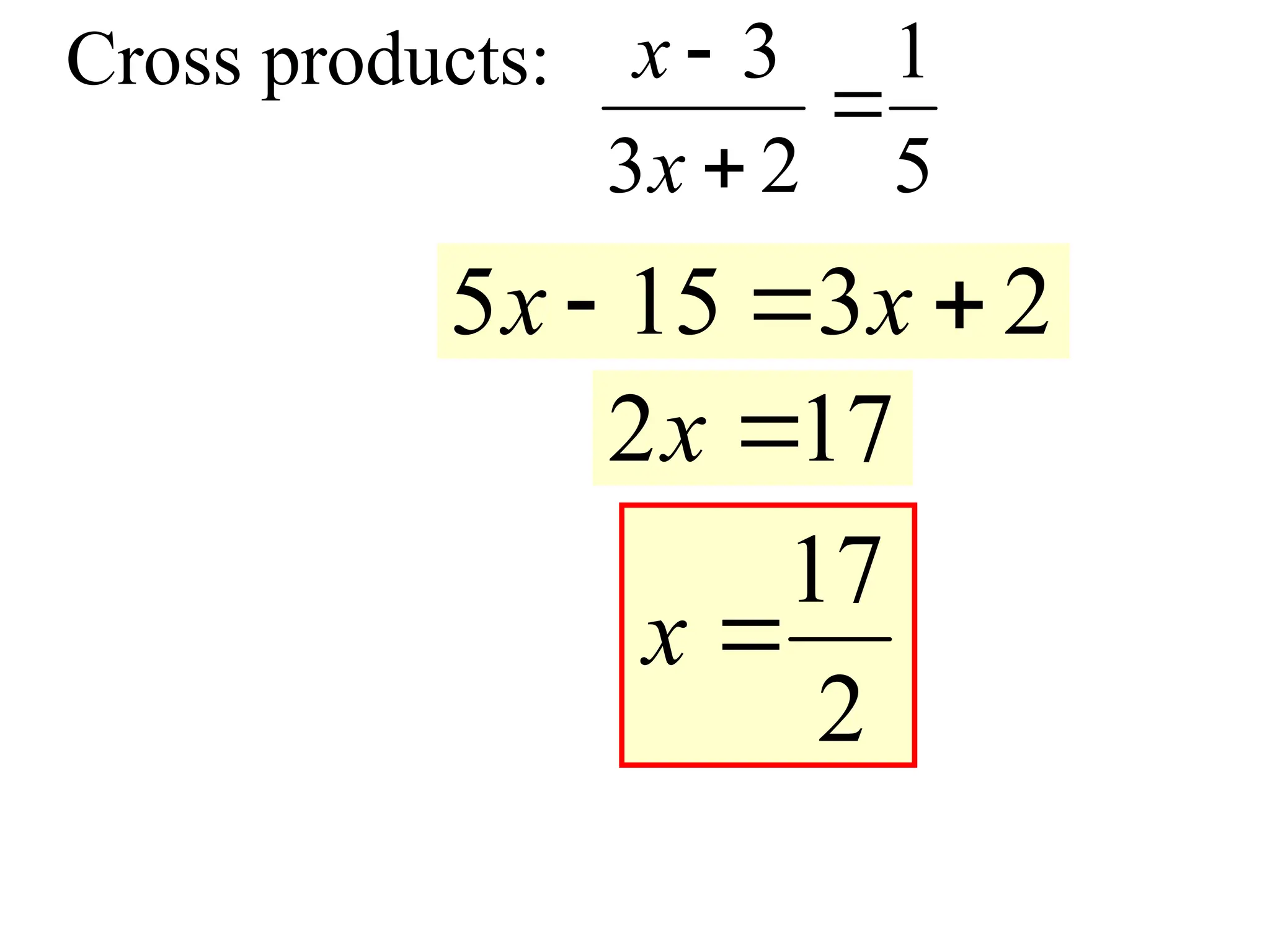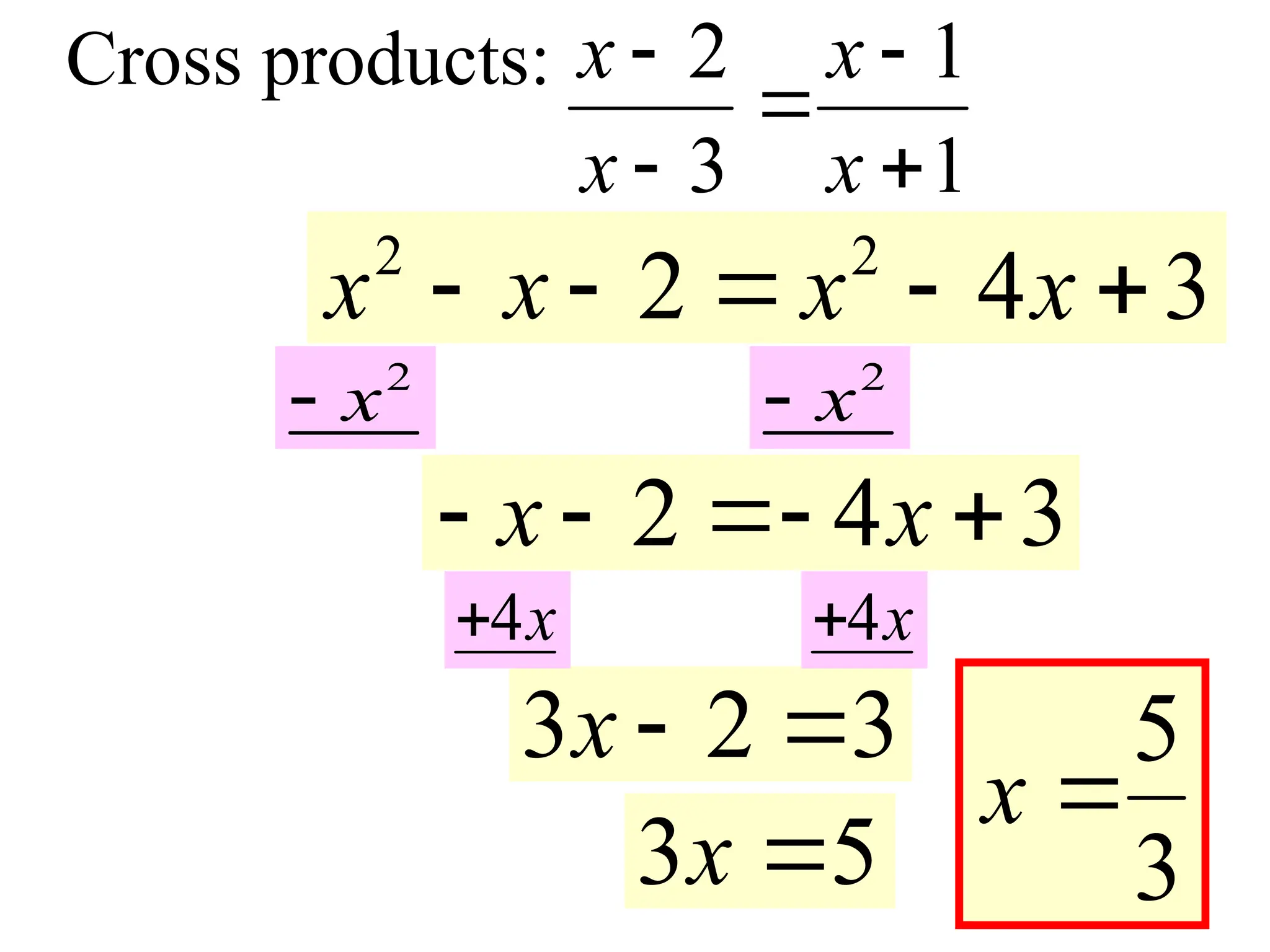Recommended
PPTX
Solving rational equations
PPT
Solving Rational Equations-General Mathematics
PPT
Solving Fractional Equations - Quadratic.ppt
PPT
Rational Equation for Grade 11 studentss
PPTX
PDF
1.6 Other Types of Equations
PPTX
rational equation transformable to quadratic equation.pptx
PPTX
Rational Algebraic Equations Transformable to Quadratic Equation.pptx
PDF
1.6 Rational and Radical Equations
PDF
2.6 Other Types of Equations
PPTX
rationalequationtransformabletoquadratic
PDF
Solving Equations Transformable to Quadratic Equation Including Rational Alge...
PPTX
PPTX
Math 9 Rational Algebraic Equations.pptx
PPTX
PPTX
lect 22 quantitative reasoning.pptx .
PPTX
PPTX
Section 14.6 solving equations with rational expressions
PPTX
LESSON-6-solving-rational-equations-and-inequalities.pptx
PPT
Lecture 01 - Linear Equations.ppt
PPTX
PDF
Pre-Cal 20S December 17, 2008
PPTX
RATIONAL FUNCTIONS, EQUATIONS AND INEQUALITIES.pptx
PDF
PPTX
PPTX
Powerpoint presentation on rational equations
PPTX
PPT
PPTX
Punctuation & Capitalization_Presentation.pptx
PPTX
Lesson 2.1 Algebra 2.pptx iwqbadci ki cxj djjs a
More Related Content
PPTX
Solving rational equations
PPT
Solving Rational Equations-General Mathematics
PPT
Solving Fractional Equations - Quadratic.ppt
PPT
Rational Equation for Grade 11 studentss
PPTX
PDF
1.6 Other Types of Equations
PPTX
rational equation transformable to quadratic equation.pptx
PPTX
Rational Algebraic Equations Transformable to Quadratic Equation.pptx
Similar to 10_6 solving rational equations Trout 09.ppt
PDF
1.6 Rational and Radical Equations
PDF
2.6 Other Types of Equations
PPTX
rationalequationtransformabletoquadratic
PDF
Solving Equations Transformable to Quadratic Equation Including Rational Alge...
PPTX
PPTX
Math 9 Rational Algebraic Equations.pptx
PPTX
PPTX
lect 22 quantitative reasoning.pptx .
PPTX
PPTX
Section 14.6 solving equations with rational expressions
PPTX
LESSON-6-solving-rational-equations-and-inequalities.pptx
PPT
Lecture 01 - Linear Equations.ppt
PPTX
PDF
Pre-Cal 20S December 17, 2008
PPTX
RATIONAL FUNCTIONS, EQUATIONS AND INEQUALITIES.pptx
PDF
PPTX
PPTX
Powerpoint presentation on rational equations
PPTX
PPT
More from psyrillejosephhurtad
PPTX
Punctuation & Capitalization_Presentation.pptx
PPTX
Lesson 2.1 Algebra 2.pptx iwqbadci ki cxj djjs a
PPTX
COHESIVE DEVICES.pptx. english 8 quarter
PPTX
GROUP 3 - MAPEH REPORTING.pptx...................
PDF
Q2-SLM3-W3-FILIPINO.pdf learning activity sheets
DOC
THANKSGIVING-LINEUP-WPS-Office.docx......
PPTX
TSINO.pptx presentation araling panlipunan
PPTX
kabihasnan . p p t x p r e s e n t ation
PPTX
Ang Mesopotamia, na nangangahulugang lupain sa pagitan ng dalawang ilog, ay m...
PPTX
basic-algebra-q2-for-student.pptx lesson
PDF
constructing figures.pdf geometry lesson
Recently uploaded
PPTX
Safe_Spaces_Act_Modern_Presentation.pptx
PPTX
1. Prepare for the application of health survey.pptx
PPTX
ELECTRICITY SECTOR IN PHILIPHINE .pptx
PPTX
Presentation 2 - USE OF EC7 IN PLAXIS .pptx
PDF
HTML-Unit 4 css introduction hi my name is css and i am from html - CSS.pdf
PPTX
essential in computer science structure and other
PPTX
[DSC Europe 25] Andy Cotgreave - Nothing is new in analytics.pptx
PPTX
Copy of First ENGR 100 Presentation.pptx
PDF
10 PyData Piraeus Meetup: Retrieval and Matching at Scale: from embeddings to...
PDF
Kate Scrivens-OECD-Community well-being and climate risks.pdf
PPTX
Understanding Double Bar Graphs for grade 5
PPTX
Creating-Effective-Scientific-Posters (1).pptx
PDF
[DSC Europe 25] Nikola Rajovic - Hardware Technologies Under the Hood: RISC-V...
PPTX
Presentation (2).pptxbbnnnnnnnnnnnnnnnnnnn
PPTX
[DSC Europe 25] Bogdan Daniel Maruneac - AI - It starts with you.pptx
PPTX
Two Factor Authentication for CSE Students.pptx
PPTX
[DSC Europe 25] Dusan Jovicic - AI Story: From on-prem to cloud and back agai...
PPTX
Time serise forcasting of non-durble consumer goods industry
PPTX
[DSC Europe 25] Petar Zivanov - AI meets documents From chatbots to AI-powere...
PPTX
Betsi- Zero-Trust Security Securing the Modern Enterprise.pptx
10_6 solving rational equations Trout 09.ppt 1. 2. 3. Steps to solve Rational Equations
1. Find the LCD
2. Multiply every term on both sides of the
equation by the LCD over 1
3. Cross Cancel
4. Solve for the variable
a. Linear equation: get variables on one side and
constants on the other
b. Quadratic: set your equation = 0 and factor.
4. Extraneous Solutions
• When both sides of the equation are mult by
a variable, the equation is transformed into a
new equation and may have an extra
solution.
• Check each solution in the original rational
equation
• Make sure that your answer does not make
the denominator 0
5. Solving Rational Equations
Solving Rational Equations
Multiply both sides of the equation
by the LCM of the denominators.
x
x
4
1
1
Least Common Multiple: Each
factor raised to the greatest
exponent.
x
x 4
LCM is 4
x x
x
x
4
x
x
4
x
2
4 x
2
6. 7. 8. 9. 10. 11. 12. Cross products
Short cut:
7 1
2 4
x
x
4 7
x
extraneous solution?
1 2
x
4 28 2
x x
1x
1x
3 28 2
x
3 30
x
10
x
13. 14. 15. Cross products: 2 1
3 1
x x
x x
2
2
x x
2
4 3
x x
2
x
2
x
2 4 3
x x
3 2 3
x 5
3
x
4x
4x
3 5
x
16.