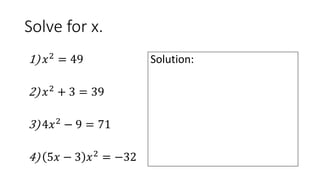Embed presentation
Downloaded 13 times







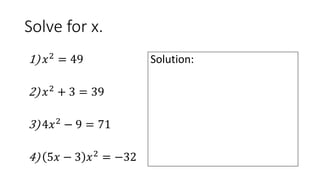
This document discusses quadratic equations and functions. It explains that a quadratic equation is an equation of degree 2 that can be written in standard form as ax2 + bx + c = 0. It provides examples of quadratic equations and shows how to write equations in standard form. The document also discusses several methods for solving quadratic equations, including factoring, graphing, completing the square, and using the quadratic formula. It introduces the square root principle for solving equations of the form x2 = a.