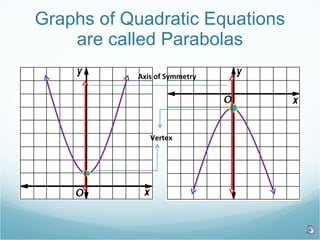
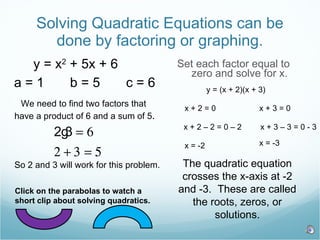
The document discusses graphing and solving quadratic equations. It defines key terms like parabolas, vertices, and axes of symmetry. It provides examples of using the quadratic formula to find the vertex and shows how to factor and set factors equal to zero to solve quadratic equations and find their roots.

1. Module 11 Topic 1 Graphing and Solving Quadratic Equations Goal 4: The learner will use relations and functions to solve problems and justify results. Objective 4.02: Graph, factor, and evaluate quadratic functions to solve problems.

2. Graphs of Quadratic Equations are called Parabolas Vertex Axis of Symmetry

3. y = ax 2 + bx + c Click on the parabola below to watch a short clip on graphing quadratics. a is a coefficient that determines if the parabola opens upward or downward a , b and c are used to find the vertex using the following formula Example 1: Determine if the parabola for the following functions open upward or downward. a) y = x 2 + 4x - 6 The graph opens upward because the value of a is 1 which is positive. b) y = -3x 2 + 6x – 2 The graph opens downward because the value of a is -3 which is negative.

4. Example 2: Find the Vertex Let’s identify a, b and c Use the vertex formula to find the vertex. y = x 2 – 6x + 4 a = 1 b = -6 c = 4

5. Example 3: Find the Vertex when b = 0 Let’s identify a, b and c Use the vertex formula to find the vertex. y = -3x 2 + 6 a = -3 b = 0 c = 6

6. Solving Quadratic Equations can be done by factoring or graphing. Set each factor equal to zero and solve for x. y = x 2 + 5x + 6 a = 1 b = 5 c = 6 We need to find two factors that have a product of 6 and a sum of 5 . So 2 and 3 will work for this problem. Click on the parabolas to watch a short clip about solving quadratics. y = (x + 2)(x + 3) x + 2 = 0 x + 2 – 2 = 0 – 2 x = -2 x + 3 = 0 x + 3 – 3 = 0 - 3 x = -3 The quadratic equation crosses the x-axis at -2 and -3. These are called the roots, zeros, or solutions.