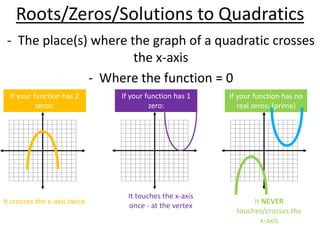
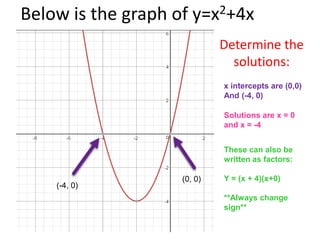
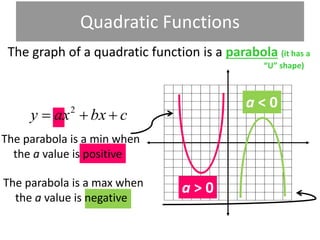
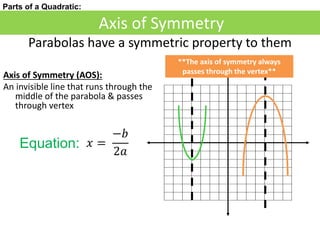
This document discusses key properties of quadratic graphs and functions including: 1) The standard form of a quadratic function is ax^2 + bx + c. The a value determines the width and whether there is a maximum or minimum. 2) The vertex is the maximum or minimum point, which can be found using the formula x = -b/2a. 3) The axis of symmetry is the line that passes through the vertex and the parabola is symmetric about this line. The axis of symmetry is defined by the equation x = -b/2a.

1. Quadratic Graphs & their Properties
Examples:
cbxaxy  2Standard form of
A quadratic function
Quadratic Term
**Determines
width, max/min**
Linear Term Constant Term
**y-intercept**
a =
b =
c =
a =
b =
c =
a =
b =
c =
23 2
 xxy 82
 xy 2
5xy 
3 1 -5
-1 0 0
-2 -8 0

2. cbxaxy  2
The parabola is a min when
the a value is positive
a > 0The parabola is a max when
the a value is negative
a < 0
Quadratic Functions
The graph of a quadratic function is a parabola (it has a
“U” shape)

3. Vertex: The maximum or minimum point of a parabola
(where the parabola changes directions). It is written as an ordered pair (x,y)
A min can be found when the parabola opens up or when a > 0
A max can be found when the parabola opens down or when a < 0
This is the lowest point so it is the vertex & it
Is a MINIMUM
This is the highest point so it is the vertex
& it is a MAXIMUM
Parts of a Quadratic:

4. Axis of Symmetry (AOS):
An invisible line that runs through the
middle of the parabola & passes
through vertex
Axis of Symmetry
Parabolas have a symmetric property to them
**The axis of symmetry always
passes through the vertex**
Parts of a Quadratic:
𝑥 =
−𝑏
2𝑎
Equation:

5. Vertex & Axis of Symmetry
Vertex is the Max or Min of a parabola
The AOS is the invisible line that passes through the vertex. It
is also an equation.
1. Find AOS: 2. Find Vertex:
962
 xxy
𝑥 =
−𝑏
2𝑎
𝑥 =
−(−6)
2(1)
𝑥 =
6
2
𝑥 = 3
a b c
𝑦 = 𝑥2
− 6𝑥 + 9
𝑦 = ( )2
−6( ) + 9
𝑦 = (3)2−6( 3) + 9
𝑦 = 9 − 18 + 9
𝑦 = 0
Vertex: (3,0)

6. Roots/Zeros/Solutions to Quadratics
- The place(s) where the graph of a quadratic crosses
the x-axis
- Where the function = 0
If your function has 2
zeros:
It crosses the x-axis twice
If your function has 1
zero:
It touches the x-axis
once - at the vertex
If your function has no
real zeros: (prime)
It NEVER
touches/crosses the
x-axis

7. Below is the graph of y=x2+4x
Determine the
solutions:
(-4, 0)
(0, 0)
x intercepts are (0,0)
And (-4, 0)
Solutions are x = 0
and x = -4
These can also be
written as factors:
Y = (x + 4)(x+0)
**Always change
sign**

8. Find the solution to each factored
quadratic
1. Y = (x – 5)(x+ 2) --- set each factor = 0 & solve
x – 5 = 0 x + 2 = 0
+5 +5 - 2 -2
x = 5 x = -2
2. Y = (2x + 5)(x – 4) – set each factor = 0 & solve
2x + 5 = 0 x – 4 = 0
-5 -5 + 4 + 4
2x = -5 x = 4
x = -5/2