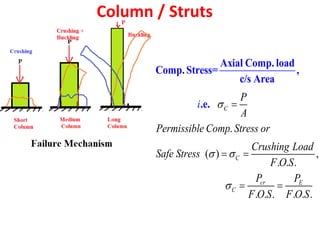
1) The document discusses column theory and different types of columns. It defines a column as a vertical compression member that carries axial loads. 2) It describes three types of columns: short columns fail due to crushing, medium columns fail due to buckling or crushing, and long columns always fail due to buckling. 3) The document presents Euler's theory and Rankine's theory as two methods to calculate the critical buckling or crippling load of columns, with Euler's theory used for long columns. It provides Euler's formula and explains key terms like effective length and slenderness ratio.

1. Sub- Solid Mechanics
Axially and Eccentrically Loaded Columns
Lect. 1 Introduction to Column theory
Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423603
An Autonomous Institute, Affiliated to Savitribai Phule Pune University, Pune
ISO 9001:2015 Certified, Approved by AICTE, Accredited by NAAC (A Grade) & NBA
Department of Civil Engineering
Prepared by:
Dr. Ghumare S. M.
Asso Professor, Civil Engg. Department,

2. Column / Struts
Introduction:
 Column is a vertical compression member generally used
to carry compressive axial loads.
 Steel Column- Stanchion
 Wooden Column- Post
 Concrete column- R..C.C Column
 Masonry columns- Pillars
Column may fail due to buckling, crushing or due to both.
Types of Columns:
1. Short Column- Short column fails due to excessive
crushing load.
2. Medium Column- Medium column fails due to buckling
or crushing.
3. Long Column- Long column always fails due to buckling
only.

3. Column / Struts
Types of Columns:
1. Short Column- Fails by crushing load.
2. Medium Column- Fails by crushing or buckling.
3. Long Column- Fails by buckling only.
Long columns fails by buckling
only.
Hence the load at which the
long columns fails is called as
Buckling Load or Crippling load
or Critical load.
Axial Comp. load
Comp. Stress= ,
c/s Area
C
P
A
 

4. Column / Struts
.
( ) ,
. . .
. . . . . .
Axial Comp. load
Comp.Stress= ,
c/s Area
.e. C
C
cr E
C
P
A
Permissible Comp Stress or
Crushing Load
Safe Stress
F O S
P P
F O S F O S
i 
 


 
 

5. Methods of analysis of Buckling or
Crippling load
Critical buckling Load can be calculated using
two methods.
1. Euler’s Theory or Euler’s Column Theory
(Used only for Long Columns)
2. Rankine’s Theory or Rankine’s Column Theory
(Used for Short as well as Long Columns)

6. Euler’s Theory or Euler’s Column Theory
(Used only for Long Columns)
 Assumptions in Euler’s Theory
1. Column is axially loaded and perfectly straight.
2. Column is made up of homogeneous, isotropic, perfectly
elastic material and obeys Hooke’s Law
3. The self weight of column is negligible or neglected.
4. The failure of the column is due to buckling only
5. Length of the column is very large compare to c/s
dimensions. (Lateral dimensions)

7. Sign Convention

8. Euler’s Formula to find Buckling Load
(Used for Long Columns)
 Euler’s Formula
2
2
min
2 2
m
mi
in
n
, .
. . x
E
x
e e
e
yy
yy
Where Effective length of the Column
It depends on End contions
Minimum M I Minimum of I and I
Generally I I
Modulus of Elastic
E I
E I
P
L L
L
I
E ity





 
 


9. .
.
Effective Length (Le)
Definition: It is the length between the two points
of zero Bending moments or
It is the length of an equivalent column of the same material
and c/s with both ends hinged and having same value of
crippling load.

10. Effective Length (Le)
Sr.
No.
End Condition Eff. Length Euler’s Formula
1 Both Ends Fixed
Le = L/2
2 One end is Fixed
and Other End
Hinged
Le = L/
3 Both Ends Hinged
Le= L
4 One end is Fixed
and Other is free Le= 2L
2
min
2
4
E
E I
P
L


2
min
2
2
E
E I
P
L


2
min
2
E
E I
P
L


2
min
2
4
E
E I
P
L



11. .
.
Slenderness Ratio ( )
Definition: It is the ratio of effective length to radius
of gyration .
,
here k r Radious of gyration
 
Le Le
k r
  
Column always buckles about axis of least resistance
2 2
I
,
I
; I
min min
From defination,
Radius of Gyration(k or r ),
k or r
k
A
Ak
A

  

12. .
.
Slenderness Ratio ( )
 
 
2 2 2
2
min
2 2
2
2
2
2 2
2
I
, , ,
/
/
,
( )
( )
Using Euler's Formula,
Buckling or Crippling Stress E
E E
e
E
e
e
E
E
e
E I E Ak
P Ak P
L L
L
E A
P where Slenderness Ratio
k
L
k
E A
L k
P E
A
P
A L
t t n
A
k
u he








   
 
 
 
 
  
    

13. .
.
Slenderness Ratio ( )
 
 
 
2
2
2 5 2 5
2
2
, 320
/
2 10 2 10
320 , / ,
320
/
/ 78.5 80
. . 80, ' ,
80
( )
'
, ,
Buckling or Crippling Stress c
E c
e
e
e
e
E
E
for Mild steel mpa
L k
X X X X
L k
L k
L k
i e For is less than Euler s formula is not applicable
Long Column
or
Euler s formula is a


 
 




 
 
  

8
: '
0, ,
pplicable for Long column
Limitaions Euler s formula is not applicable fo
Shor
r sho
t Col
rt co
u n
mn
m
lu
 

14. .
.
Stability conditions for Axially Loaded Columns
1. Stable Equilibrium: When axial load P is smaller than
critical load (failure load) then column remains straight
and undergoes only axial compression. i.e. lateral
deflection is zero.
2. Neutral Equilibrium: If axial load P increases
gradually, the stage will reach that column will buckle or
bent but will not regain its original shape.
3. Unstable Equilibrium: If axial load P further
increased, the column will be unstable and collapse due
to bending or buckling.
,
cr
P
P P and
A
 
cr
P P

cr
P P


15. Stability conditions for Axially Loaded Columns
Stable Equilibrium Neutral Equilibrium Un-Stable Equilibrium

16. Thank You