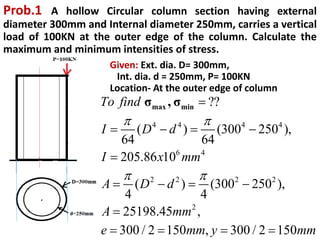
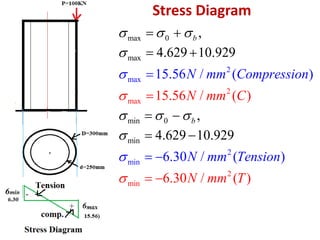
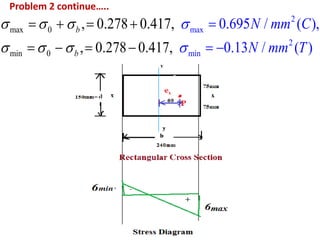
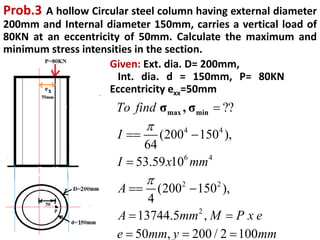
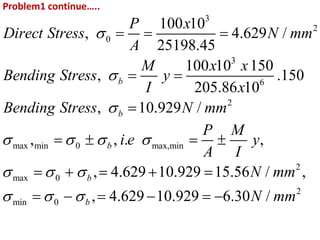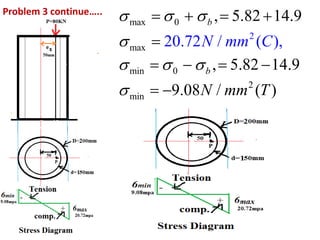
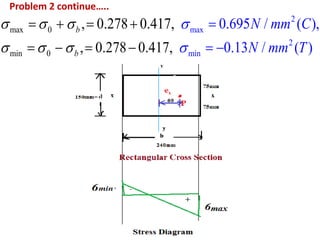
1) Eccentrically loaded columns experience both direct stress from the applied load as well as bending stress due to the eccentricity of the load. The maximum and minimum stresses are calculated as the sum and difference of these direct and bending stresses. 2) Three examples of eccentrically loaded columns are provided: a hollow circular column, a rectangular column, and another hollow circular column. The maximum and minimum stresses are calculated for each example by determining the direct and bending stresses from the given load, dimensions, and eccentricity, and summing or differencing as required. 3) Stress diagrams are shown for each example, indicating the variation of compressive and tensile stress across the cross section due to the eccentric

1. Sub- Solid Mechanics
Eccentrically Loaded Columns
Lect. 5 Direct & Bending Stresses
Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423603
An Autonomous Institute, Affiliated to Savitribai Phule Pune University, Pune
ISO 9001:2015 Certified, Approved by AICTE, Accredited by NAAC (A Grade) & NBA
Department of Civil Engineering
Prepared by:
Dr. Ghumare S. M.
Asso Professor, Civil Engg. Department

2. Direct and Bending Stress
0
, ,
,
max min 0 b
max min
Max,Min
Eccentric load produces the
Direct stress as well as
bending stress.
σ , =σ ± σ ,
P M
σ , = ± y,
A I
P 6e
σ = 1±
A b
b
P
Direct Stress
A
M
Bending Stress y
I




 
 
 

3. Prob.1 A hollow Circular column section having external
diameter 300mm and Internal diameter 250mm, carries a vertical
load of 100KN at the outer edge of the column. Calculate the
maximum and minimum intensities of stress.
Given: Ext. dia. D= 300mm,
Int. dia. d = 250mm, P= 100KN
Location- At the outer edge of column
4 4 4 4
6 4
2 2 2 2
2
??
( ) (300 250 ),
64 64
205.86 10
( ) (300 250 ),
4 4
25198.45 ,
300 / 2 150 , 300 / 2 150
max min
σ , σ
To find
I D d
I x mm
A D d
A mm
e mm y mm
 
 

   

   

   

4. 3
2
0
3
6
2
max min 0 max,min
2
max 0
min 0
100 10
, 4.629 /
25198.45
100 10 150
, .150
205.86 10
, 10.929 /
, , . ,
, 4.629 10.929 15.56 / ,
,
b
b
b
b
b
P x
Direct Stress N mm
A
M x x
Bending Stress y
I x
Bending Stress N mm
P M
i e y
A I
N mm



   
  
  
  
 

   
    
  2
4.629 10.929 6.30 /
N mm
   
Problem1 continue…..

5. Stress Diagram
2
max
2
mi
2
max
2
mi
max 0
max
min 0
m
n
n
in
15.56 / ( )
6.30 / (
15.56 / ( )
6.30 / ( )
,
4.629 10.929
,
4.629 10.
)
929
b
b
N mm C
N mm Compression
N mm Te
N
n
m
s
m T
ion



  

  



 

 
 
 
 
 

6. Prob.2 A rectangular column of size 240mm x 150mm,is
subjected to a vertical load of 10KN placed at eccentricity of
60mm in a plane bisecting 150mm side. Determine the maximum
and minimum stress intensities in the section.
Given:
Rect. Column = 240x 150mmmm,
Vertical load P= 10KN, ex = 60mm,
Plane bisecting 150mm side. Load cause
the moment @y-y axis. Consider Iyy
3 3
6 4
2
??
150 240
12 12
172.8 10
240 150 36000 ,
60 ,
240 / 2 120
max min
σ , σ
yy
yy
x
To find
DB X
I
I x mm
A x mm
e mm
y mm

 

 

 

7. 3
2
0
3
6
2
max min 0 max,min
2
max 0
min 0
10 10
, 0.278 /
36000
10 10 60
, .120
172.8 10
, 0.417 /
, , . ,
, 0.278 0.417 0.695 / ,
, 0.278 0.
b
b
b
b
b
P x
Direct Stress N mm
A
M x x
Bending Stress y
I x
Bending Stress N mm
P M
i e y
A I
N mm



   
  
  
  
 

   
    
    2
417 0.13 /
N mm
 
Problem 2 continue…..

8. max 0
m
2
max
2
m
in 0 in
0.695 / ( ),
, 0.278 0.417,
, 0.278 0.417, 0.13 / ( )
b
b
N mm C
N mm T


  
  
   
  

 

Problem 2 continue…..

9. Prob.3 A hollow Circular steel column having external diameter
200mm and Internal diameter 150mm, carries a vertical load of
80KN at an eccentricity of 50mm. Calculate the maximum and
minimum stress intensities in the section.
Given: Ext. dia. D= 200mm,
Int. dia. d = 150mm, P= 80KN
Eccentricity exx=50mm
4 4
6 4
2 2
2
??
(200 150 ),
64
53.59 10
(200 150 ),
4
13744.5 ,
50 , 200 / 2 100
max min
σ , σ
To find
I
I x mm
A
A mm M P x e
e mm y mm



 

 
 
  

10. 3
2
0
3
6
2
max min 0 max,min
2
max 0
min 0
80 10
, 5.82 /
13744.5
80 10 50
, .100
53.59 10
, 14.9 /
, , . ,
, 5.82 14.9 20.72 / ,
, 5.82 14.9
b
b
b
b
b
P x
Direct Stress N mm
A
M x x
Bending Stress y
I x
Bending Stress N mm
P M
i e y
A I
N mm



   
  
  
  
 

   
    
     2
9.08 /
N mm

Problem 3 continue…..

11. max 0
max
min 0
2
min
2
20.72 / ( ),
, 5.82 14.9
, 5.82 14.9
9.08 / ( )
b
b
N mm C
N mm T
  

  

   

   
 
Problem 3 continue…..

12. max 0
m
2
max
2
m
in 0 in
0.695 / ( ),
, 0.278 0.417,
, 0.278 0.417, 0.13 / ( )
b
b
N mm C
N mm T


  
  
   
  

 

Problem 2 continue…..

13. Next lecture numerical on stresses
at corner of columns
Thank you