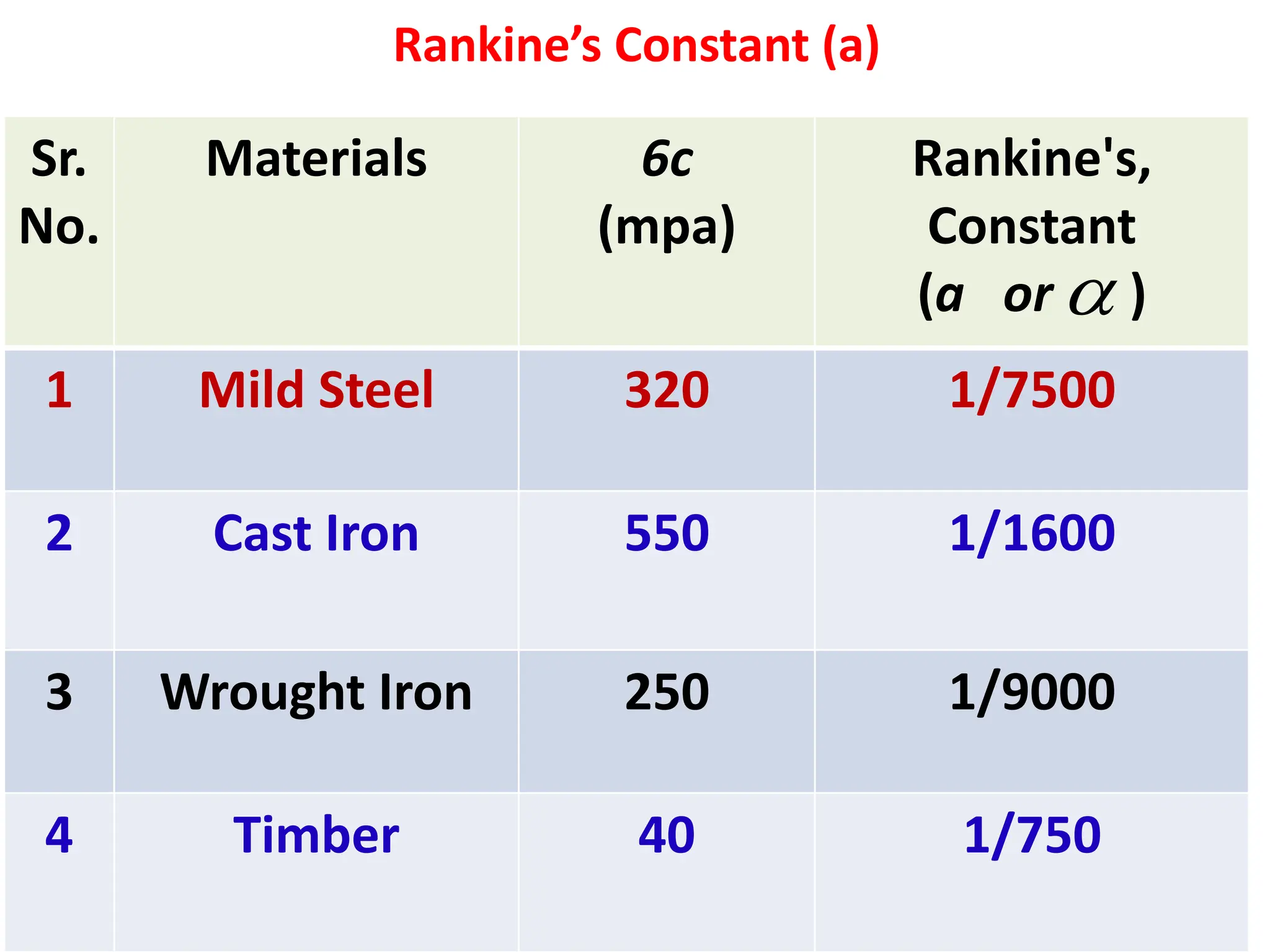
1) Rankine's formula considers both compressive stress and buckling stress in columns. It can be used for short as well as long columns with a slenderness ratio greater than 80. 2) The formula is: P = σA + [σA(λ2 - 1)/(1 + aλ2)] where P is the Rankine buckling/crippling load, σ is the crushing stress, A is the cross-sectional area, λ is the slenderness ratio, and a is the Rankine constant which depends on the material. 3) Several examples are provided to demonstrate calculating the safe load of columns using Rankine's formula for different end conditions and materials like steel

1. Sub- Solid Mechanics
Axially and Eccentrically Loaded Columns
Lect. 4 Rankine’s Formula
Sanjivani Rural Education Society’s
Sanjivani College of Engineering, Kopargaon-423603
An Autonomous Institute, Affiliated to Savitribai Phule Pune University, Pune
ISO 9001:2015 Certified, Approved by AICTE, Accredited by NAAC (A Grade) & NBA
Department of Civil Engineering
Prepared by:
Dr. Ghumare S. M.
Asso Professor, Civil Engg. Department

2. Rankine’s Formula to find the Buckling or Crippling load
Rankine’s Formula: Rankine’s formula is used for short as
well as for long columns where slenderness ratio is grater
than 80.
It considers stress due to compressive load as well as
buckling (bending).
2
2
1 1 1
, ,
' ,
,
'
R C E
R
C c
E E
e
Hence
P P P
P Rankine s Crippling load
P X A Crushing load acting short column
E I
P Euler s Crippling Load X A
L



 

 
  

3. Rankine’s Formula
2
2
.
R C E
E C C E C
R
E C
R C E E C
E
C
R
C
E
c
2
C c E 2
e
c
c c
R 2
C
R 2
e
c c e
2 2
E
2
e
1 1 1
Hence, = + ,
P P P
P +P P P P
1
= , P = = ,
P +P
P P P P +P
P
P
P = ,
P
1+
P
σ A σ A σ A I
P = = = , ,k= , Put, I
P σ A σ A L A
1+
π E I
1+ 1+
put P =σ A & P =
L
σ A
P = =Rankine's Formu
L
1+
π E I
P π E
k
A
a
k
L
here A
in Eq
k
 
 


 
 
 
 
&
2
e
c
σ
here, a=
π E
L
la
k

 

 
 

4. ' :
c
R 2
e
e c
2
R
c
e
σ A
P = , -----------(A)
L
1+a
k
L σ
In Eq. (A), =λ(Slenderness Ratio) & a=
k π E
here,P =Rankine's Buckling or Crippling Load
σ =Crushing stress,
L =Effective length based on End condition,
k =Radiou
Rankine Formula
 
 
 
 
 
 
I
s of Gyration= ,
A
a=Rankine's Comstant depends on type of material,
A=Area of Column
Rankine’s Formula

5. Rankine’s Constant (a)
Sr.
No.
Materials 6c
(mpa)
Rankine's,
Constant
(a or )
1 Mild Steel 320 1/7500
2 Cast Iron 550 1/1600
3 Wrought Iron 250 1/9000
4 Timber 40 1/750


6. Numerical on Rankine’s formula
2
1
c
R
e
A
P
L
a
k


 
  
 

7. Problem 1: A column section having external dia. 200mm
and thickness 20mm is used as column. The length of
column is 4.5m. It is fixed at both ends. Find the safe load
using Rankine’s formula. F.O.S.= 4. Take 6c=550mpa &
a=1/1600
Given, D=200mm, t=20mm, 6c=550mpa, P=60KN=60x103N,
L=4.5m=4500mm, F.O.S.= 4, a=1/1600, PR=????
   
   
2 2 2 2
4 4 4
2
6
4
3
4
11.309 10 ,
46.36 1
200 160
4 4
200 160
64
0
,
4
A D d
I
A X mm
I X mm
D d
 
 

 

 
   

8. Problem 1 Continue……
 
 
6
3
3
/ 2 4500 / 2 2250 ,
46.36 10
,
11.309 10
2500
64.
sin '
03
550 11.309
64
1
.03
35
,
.
0
14
1
(
1
):
End Cond.:Both ends fixed e
C
R
R
L L mm
I X
Radious ofGyration
A X
Le
Slenderness Ratio
k
A x x
P
Le
a
k
U g Rankine s Formula Fi
k
nd
mm
P


  
  
  
 
  
  
 
 
2
3
6
6
877.6
3.51 10 ,
1
35.14
1600
3.51 10
,
4
1 10 877.61
R
x N
P
Critical Load x
Safe Load
FO
Safe Load
S FOS
x N KN

 
 


9. Problem 2: A Strut of length 2m is made of Aluminium
tube that has 32mm outer dia. and 4mm wall thickness. Use
FOS=2, a=1/7500 & 6c=550mpa. Determine load for
following conditions. 1) When both ends fixed 2) Both ends
Hinged.
Given, L = 2m = 2000mm, d=32mm, d= 24mm, FOS=2,
a=1/7500 , 6c=550mpa. PR=???
Case: I- Both Ends Fixed Eff. Length, Le=L/2=1000mm,
   
   
2 2 2
2
3 4
2
4 4 4 4
32 24
4 4
32 24 200 160 ,
64
351.85 ,
35.18 1
4
0
A mm
I X mm
A D d
I
 
 
   
   



10.  
 
 
3
3
2
35.18 10
,
351.85
1000
100,
10
550 351.85
82.936 10 ,
1
1 100
1
7
sin
10
82.9
' , (
500
3
)
6
:
C
R
R
R
Case I Both Ends Fixed
U g R
I X
Radious ofGyration
A
Le
Slenderness Ratio
k
A x
ankine s Formul
P x N
Le
a
k
Safe Load
k mm
a
N
F n
K
i d P
P


  
  
  
  
  
 



82.936
41.52 ,
R
P
KN
 
Problem 2 Continue……

11.  
 
 
3
3
2
35.18 10
,
351.85
200
s
0
200,
10
550 351.85
30.55 10 ,
1
i
1 200
1
750
n ' , ( )
, 2000
10
30.55
0
:
R
R
C
R
Case II Both Ends Hinged
I X
Radious ofGyration
A
Le
Slenderness Ratio
k
A x
P x N
L
U g Rankine s Formul
e
a
k
Le L mm
k
a F n P
mm
P
i d


  
  
  
 
  



 
 
30.55
15.25 ,
R
P
Safe Load KN
KN
  
Problem 2 Continue……

12. Problem 3: Compare the Crippling load given by Euler’s
formula & Rankine’s formula for circular c/s of 40mm outer
dia. and 2m length. Take, a=1/7500, Yield stress 6c=300mpa
and E=200Gpa. Assume both ends Hinged.
Given, D=40mm, a=1/7500 , PR=???, Yield stress 6c=300mpa
Both Ends Hinged, Eff. Length, Le=L=2000mm, E=200Gpa.
   
   
2
3
2 2
4 4 4
40
4 4
40 40 ,
64 6
1256.4
125.6 10
4
1
125.6 10
1256.4
0 ,
2000
200
10
e
mm
X m
A D
I
I
k mm
A
L
k
m
X
 
 

 
 
  
 




13. Problem 3 Continue……
2
min
2
2 3 3
2
2
2
,
200 10 125.6 10
(2000)
300 1256.4
,
1
1 (200)
1 7500
62.0
62.013
59.525
1
5
,
3
1. Using Euler's Formula,
2. Using Rankine's Formula,
Compare Euler's Load and Rankine's Load:
E
e
E
c
R
e
E
R
KN
E I
P
L
X X X X
P
A X
P
L
a
k
P
P
KN




 
  
  
  
 
 1.0418
9.525


14. Problem 4: A hollow cast iron column whose outside
diameter is 250mm and 15mm thickness. Column is 4.5m
long and fixed at both ends. Calculate the safe load by
Rankine’s Formula when Factor of Safety is 4. Also calculate
the slenderness ratio and Rankine’s Crippling load.
Take E=94Gpa, a=1/1600 and 6c=550mpa
 
6 4
1. . 76.7185 10 ,
2. 83.254 ,
3. 27.026
4. ' P 41.82 ,
5. P 10.45
:
e
R
R
M I I X mm
Radious of Gyration k mm
L
Slenderness Ratio
k
Rankine Formula KN
Safe loa
A
d KN
ns  

 

 
 



15. Next Lecture Eccentrically Loaded
Column
(Direct and Bending Stresses)

16. Thank You