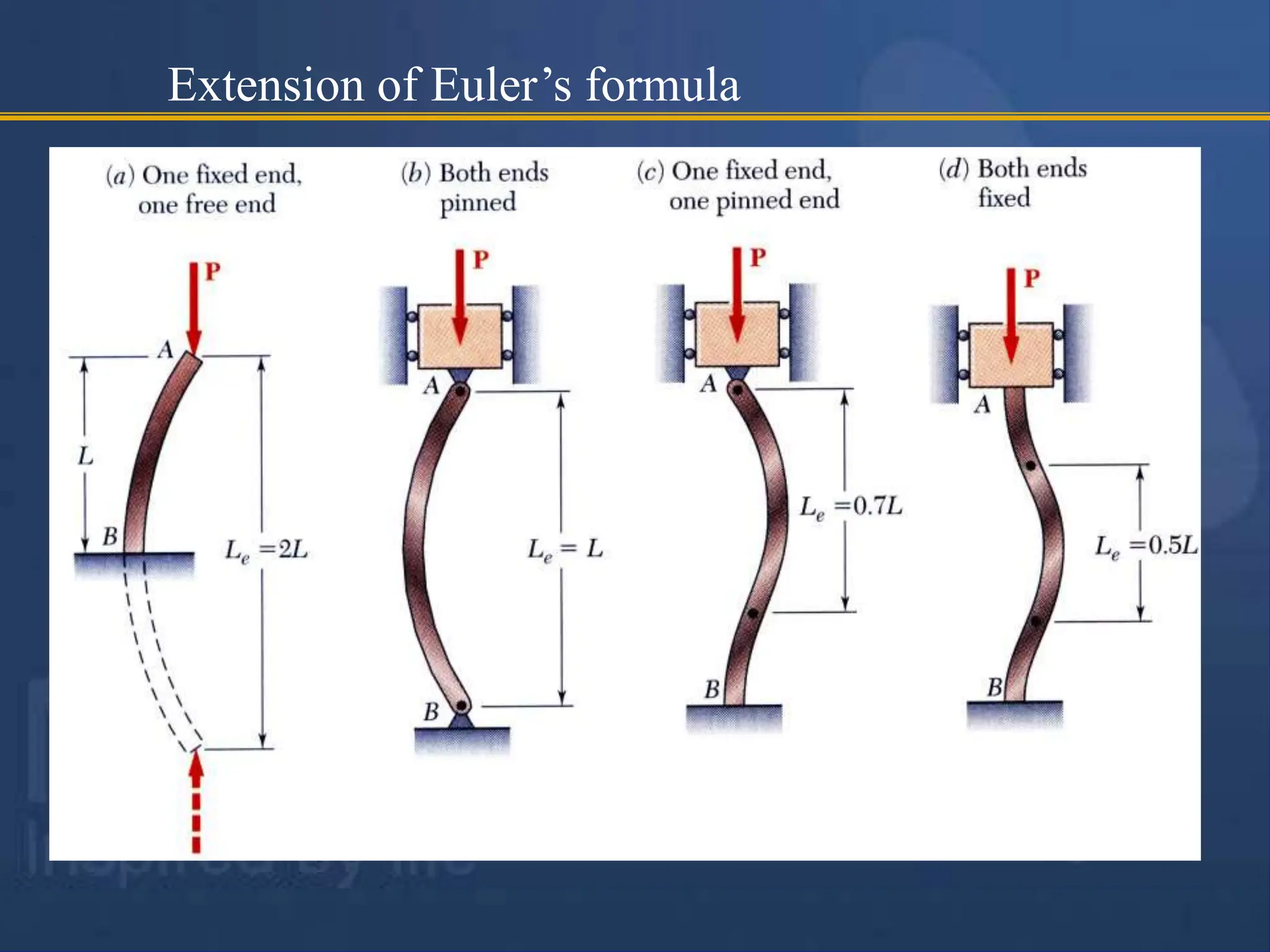
The document discusses the stability of columns and struts, defining their roles as structural members subjected to compression. It elaborates on various equilibrium states (stable, neutral, unstable), buckling load, safe load, and failure modes for short and long columns, as well as providing Euler's theory and formulas related to critical load and slenderness ratio. Numerical examples illustrate the application of Euler's formula in determining safe loads for different column configurations.

1. Stability
of
columns

2. Columns and struts: Structural members subjected to
compression and which are relatively long compared to
their lateral dimensions are called columns or Struts.
Generally, the term column is used to denote vertical
members and the term strut denotes inclined members
Examples: strut in a truss, Piston rods, side links in
forging machines, connecting rods etc.

3. Stable, Neutral and unstable Equilibrium
Stable equilibrium: A stable equilibrium is one in which a
body in static equilibrium on being displaced slightly,
returns to its original position and continues to remain in
equilibrium.

4. Neutral equilibrium: A neutral equilibrium is one in
which a body in equilibrium, on being displaced does
not returns to its original position, but its motion stops
and resumes its equilibrium state in its new position.

5. Unstable equilibrium: An unstable equilibrium is one in
which a body in equilibrium on being slightly disturbed,
moves away from its equilibrium position and loses its
state of equilibrium.

6. Buckling Load: The maximum load which a column can support
before becoming unstable is known as buckling load or crippling
load or critical load
The buckling takes place about the axis having
minimum radius of gyration or least moment of
inertia.
At this stage, the maximum stress in the column will be less than the
yield stress (crushing stress) of the material.

7. Safe load: It is the load to which a column is subjected
to and is well below the buckling load. It is obtained by
dividing the buckling load by a suitable factor of safety.
safe load = buckling load / factor of safety

8. MODES OF FAILURE OF THE COLUMNS
P
P
The load carrying capacity of a short column depends
only on its cross sectional area(A) and the crushing stress
of the material(σcu). The crushing load Pu for axially
loaded short column is given by Pcu =σcu × A .
The safe load on the column is obtained by dividing the crushing
load by suitable factor of safety. i.e., Psafe =Pcu/ FS
The mode of failure of columns depends upon their lengths and
depending on the mode of failure columns are classified as
a. Short columns b. Long columns
Short Columns: A short column buckles under compression as
shown in figure and fails by crushing. The load causing failure is
called crushing load.

9. Long columns: Long columns, which are also called
slender columns, when subjected to compression,
deflects or bends in a lateral direction as shown in the
figure. The lateral deflection of the long column is
called buckling.
The load carrying capacity of long column depends upon several
factors like the length of the column, M.I of its cross–section,
Modulus of elasticity of the material, nature of its support, in
addition to area of cross section and the crushing strength of the
material.
Critical load denotes the maximum load carrying
capacity of the long column.
The long column fails when there is excessive
buckling .ie when the load on the column exceeds critical
load.

10. Short columns fails by crushing or yielding of the material under
the load P1
Long column fails by buckling at a substantially smaller load P2
(less than P1).
P
1
P
2
The buckling load is less than the crushing
load for a long column
The value of buckling load for long column is
low whereas for short column the value of
buckling load is relatively high.

11. Failure of long columns(contd)
Stress due to buckling
σb = ( M.ymax)/ I
= {(P.e). ymax}/ I
= ( P.e) / Z
Where e = maximum bending of the column
at the centre
Consider a long column of uniform cross sectional area A
throughout its length L subjected to an axial compressive
load P. The load at which the column just buckles is known
as buckling load or crippling load.
Stress due to axial load σc = P/A
P
L e

12. Failure of long columns(contd)
σmax = σc + σb
Extreme stress at centre of column will be the sum of direct
compressive stress and buckling stress
In case of long columns, the direct compressive
stresses are negligible when compared to buckling
stress. So always long columns fail due to buckling.

13. Euler’s Theory (For long columns)
Assumptions:
1. The column is initially straight and of uniform
lateral dimension
2. The material of the column is homogeneous,
isotropic, obeys Hookes law
3. The stresses are within elastic limit
4. The compressive load is axial and passes through
the centroid of the section
5. The self weight of the column itself is neglected.
6. The column fails by buckling alone

14. Euler’s Theory (For long columns)
A Bending moment which bends the
column as to present convexity
towards the initial centre line of the
member will be regarded as positive
Bending moment which bends the
column as to present concavity
towards the initial centre line of the
member will be regarded as negative
Sign convention for Bending Moments

15. Euler’s Formula for Pin-Ended Beams
(both ends hinged)
L
y x
P
P
A
B
PE =
π2E I
L2
This load is called critical or buckling load
or crippling load

16. case End condition Equivalent
length(Le)
Euler’s Buckling load
1 Both ends hinged Le=L PE= (π 2E I) / Le
2
2 One end fixed, other
end free
Le=2L PE= (π 2EI) / 4L2
3 One end fixed, other
end pin jointed
Le=L / √2 PE= 2(π 2EI) / L2
4 Both ends fixed Le=L/2 PE= 4(π 2 EI) / L2
Note: L is the actual length of respective column and Le is to be
considered in calculating Euler's buckling load

17. Extension of Euler’s formula

18. Slenderness ratio: It is the Ratio of the effective length of the
column to the least radius of gyration of the cross sectional ends of
the column.
The Effective length: of a column with given end conditions is the
length of an equivalent column with both ends hinged, made up of
same material having same cross section, subjected to same
crippling load (buckling load) as that of given column.
Slenderness ratio, λ =Le /k
Least radius of gyration, k= √ Imin/A
Imin is the least of I xx and I yy
L =actual length of the column
Le=effective length of the column
A= area of cross section of the

19. Based on slenderness ratio ,columns are classified as
short or long column.
Generally the slenderness ratio of short column is less
than 32 ,and that of long column is greater than 120.

20. Limitation of Euler's theory
Pcr
= (π 2 EI) / Le
2
But I =Ak2
∴ Pcr/A= π 2E/(Le/K)2
σcr = π2E/(Le/K)2
Where σcr is crippling stress or critical stress or stress at failure
The validity of Euler’s theory is subjected to condition that
failure is due to buckling. The Euler’s formula for crippling is
The term Le/K is called slenderness ratio. As slenderness ratio
increases critical load/stress reduces. The variation of critical stress
with respect to slenderness ratio is shown in figure 1. As Le/K
approaches to zero the critical stress tends to infinity. But this
cannot happen. Before this stage the material will get crushed.

21. ILLUSTRATIVE NUMERICAL EXAMPLES
Euler’s crippling load =PE= (π2EI) / Le 2
= [π 2 × 200 × 109 × π × (0.06)4 /64] / (1.7682)
= 401.7 ×103 N =401.4 kN
Safe compressive load = PE /3 =133.9kN
1. A solid round bar 60mm in diameter and 2.5m long is
used as a strut. One end of the strut is fixed, while its other
end is hinged. Find the safe compressive load, for this strut,
using Euler’s formula. Assume E=200GN/m2 and factor of
safety =3.
end condition: one end hinged, other end fixed
effective length Le = L /(√ 2)= 2.5/ (√ 2)= 1.768m
Solution:

22. outside diameter of the column =D =50mm
=0.05m; E=70 × 10 9N/m2
Inside diameter = ?
2.A slender pin ended aluminium column 1.8m long and of
circular cross-section is to have an outside diameter of
50mm. Calculate the necessary internal diameter to prevent
failure by buckling if the actual load applied is 13.6kN and
the critical load applied is twice the actual load. Take
Ea = 70GN/m2.
Solution:

23. End condition: pin-ended ( hinged)
Le =L =1.8m
Euler’s crippling load =PE= π 2 (EI) / Le
2
d = 0.0437m = 43.7mm
2
4
4
3
8
.
1
64
)
05
.
0
(
10
70
10
2
.
27
9
2
d








Critical load =PE = 2 × safe load (given condition)
= 2 × 13.6=27.2kN
I= π (D4-d4) /64 = π (0.054-d4) /64

24. 3. A built up beam shown in the figure is simply supported at its
ends. Compute its length, given that when it subjected to a load of
40kN per meter length. The length of column is 14.15 m. Find the
safe load, if this beam is used as a column with both ends fixed.
Assume a factor of safety of 4. use Euler’s formula. Take E =
210GN/m2.
300 mm
50 mm
1000 mm
20 mm

25. Moment of inertia of section about X-X axis,
Load =40kN/m , length of the beam = 14.15 m
= 994166 × 104 mm4= 99.41×10-4 m
12
1000
20
525
)
50
300
(
12
50
300
2
3
3
2












xx
I
Iyy = 2[ (50 × 300 3) /12] + (1000 × 20 3 ) /12
= 22567 × 10 4 mm4 = 2.25 × 10 -4 m4
Moment of inertia of section about Y-Y axis,

26. Safe load, the beam can carry as column:
End condition: Both ends fixed
PE = π 2 (EIyy) / Le
2
= (π 2 × 210 × 109 × 2.25 × 10 -4) / (7.07)2
= 9.33 × 10 6 N = 9.33 × 10 3 kN
Safe load = Pe /F.S = 9.33 × 10 3 / 4 = 2.333 × 10 3 kN
Le = L/2 = 14.15/2 = 7.07m