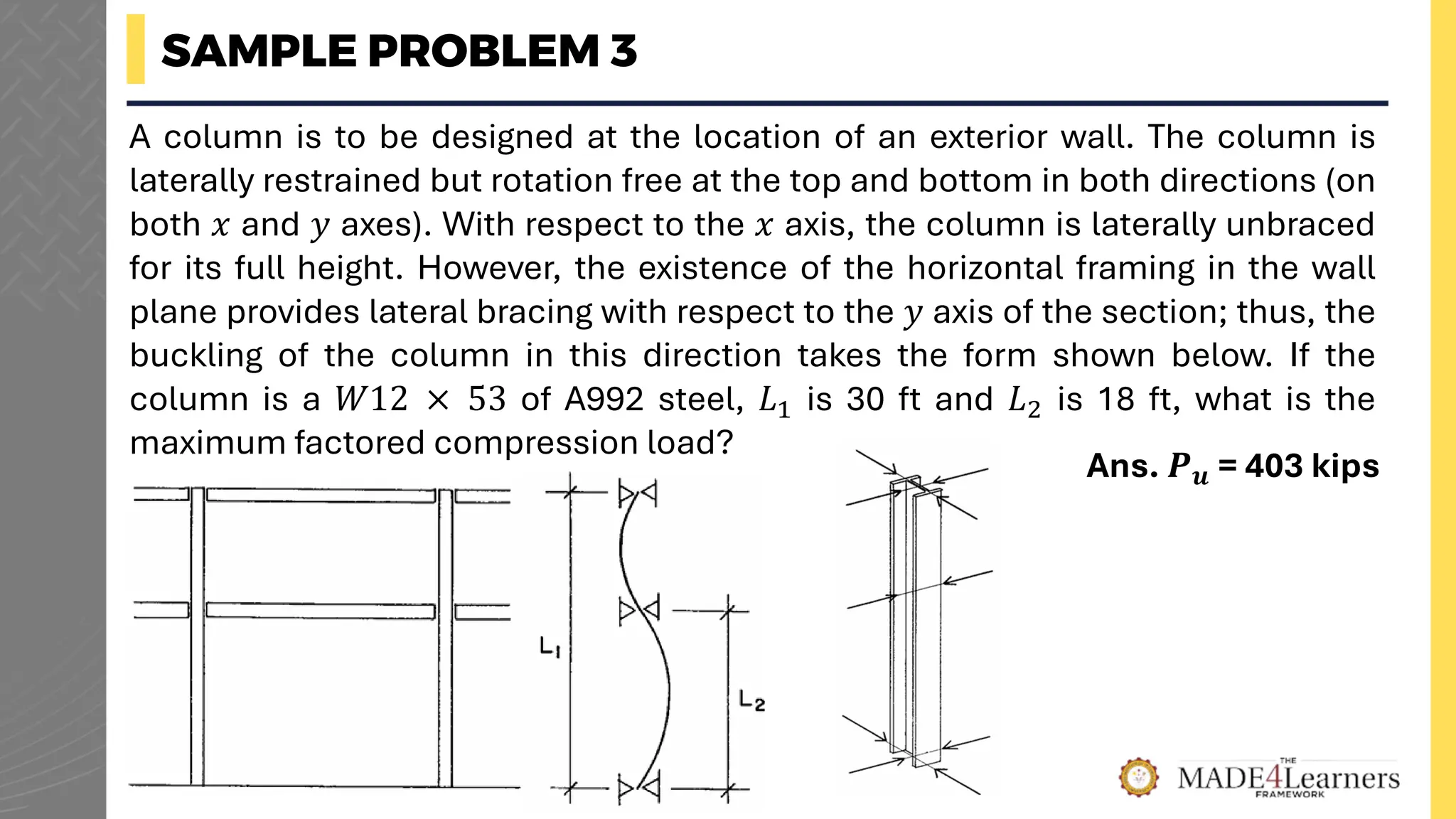
The document discusses compression members in structural engineering, particularly focusing on their behavior under axial loads and the resulting buckling phenomena. It details the critical buckling load derived from Euler's theory, including various calculations and assumptions necessary for the analysis. Additionally, it includes example problems illustrating the application of design standards and factors affecting the stability and strength of compression members in structures.

1. CE497
COMPRESSION MEMBERS
ENGR. DJ LEX YNOT
STEEL AND TIMBER DESIGN

2. COMPRESSION MEMBERS
Compression members are structural elements that are subjected only to axial
compressive forces (i.e. loads are applied along a longitudinal axis through the
centroid of the member cross section)
This ideal state is never achieved in reality because some eccentricity is
inevitable. Bending will result, but it can usually be regarded as secondary and
can be neglected if the theoretical loading condition is closely approximated
The most common type of compression member occurring in buildings and
bridges is the column, a vertical member whose primary function is to support
vertical load

3. COMPRESSION MEMBERS
Column Theory
Consider a long, slender compression member resisting a vertical load 𝑃 at the
top. If the axial load 𝑃 is slowly applied, the compression member will
ultimately become unstable and buckle about its axis with a corresponding load
called the critical buckling load.
If the member is stockier, a larger load will be required to bring the member to
the point of instability. For extremely stocky members, failure may occur by
compressive yielding rather than buckling.
Prior to failure, the compressive stress 𝑃/A will be uniform over the cross
section at any point along the length, whether the failure is yielding or buckling.
The load at which buckling occurs is a function of slenderness, and for very
slender members this load could be quite small.

4. COMPRESSION MEMBERS
Column Theory
If the member is so slender that the stress just before buckling is below the
proportional limit – that is, the member is still elastic – the critical buckling load
is given by:
𝑷𝒄𝒓 =
𝝅𝟐
𝑬𝑰
𝑳𝟐
where: E = modulus of elasticity of the material
I = moment of inertia of the cross-sectional area with respect to the
minor principal axis
L = length of the member between points of support

5. COMPRESSION MEMBERS
For the equation to be valid, member must be elastic, and its ends must be free
to rotate but not translate laterally. This end condition is satisfied by hinges or
pins.
Column Theory
This remarkable relationship was first formulated by Swiss mathematician
Leonhard Euler. The critical load 𝑃𝑐𝑟 is sometimes referred to as the Euler load
or Euler buckling load. It is the load that is just large enough to maintain the
deflected shape when the temporary transverse load is removed.

6. COMPRESSION MEMBERS
If the critical load is divided by the cross-sectional area, the critical buckling
stress is obtained:
Column Theory
𝝈𝒄𝒓 =
𝑷𝒄𝒓
𝑨
where: 𝐴 = cross-sectional area
𝑟 = radius of gyration with respect to the axis of buckling
𝐿/𝑟 = slenderness ratio
=
𝝅𝟐𝑬
(𝑳/𝒓)𝟐

7. COMPRESSION MEMBERS
Column Theory
At this compressive stress, buckling will occur about the axis corresponding to
𝑟. Buckling will take place as soon as the load reaches the value of 𝑃𝑐𝑟, and the
column will become unstable about the principal axis corresponding to the
largest slenderness ratio. This axis usually is the axis with the smaller moment
of inertia.

8. SAMPLE PROBLEM 1
A 𝑊12 × 50 is used as a column to support an axial compressive load of 145
kips. The length is 20 feet, and the ends are pinned. Without regard to load or
resistance factors, investigate this member for stability. 𝐸𝑠𝑡𝑒𝑒𝑙 = 29,000 ksi
For 𝑊12 × 50 :
Minimum 𝑟 = 𝑟𝑦 = 1.96 in.
Area, 𝐴 = 14.6 in2
Ans. Safe, F.S. = 1.92

9. SAMPLE PROBLEM 1
Solution:
Maximum
L
r =
20 ft (12 in/ft)
1.96 in
= 122.4
𝑃𝑐𝑟 =
𝜋2𝐸
(𝐿/𝑟)2
𝐴 =
𝜋2(29,000)(14.6 in2)
(122.4)2
= 278.9 kips
Because the applied load of 145 kips is less than 𝑃𝑐𝑟, the column remains stable and has an
overall factor of safety against buckling of 278.9 kips / 145 kips = 1.92.

10. COMPRESSION MEMBERS
Effective Length
The Euler equation is based on the following assumptions:
The first two conditions mean that there is no bending moment in the member
before buckling. The requirement for pinned ends, however, is a serious
limitation, and provisions must be made for other support conditions. The
pinned-end condition requires that the member be restrained from lateral
translation, but not rotation, at the ends
1. The column is perfectly straight, with no initial crookedness.
2. The load is axial, with no eccentricity.
3. The column is pinned at both ends.

11. COMPRESSION MEMBERS
Effective Length
For convenience, the equations for critical buckling load will be written as:
𝑷𝒄𝒓 =
𝝅𝟐𝑬𝑨
(𝒌𝑳/𝒓)𝟐
where: 𝑘𝐿 = effective length
𝑘 = effective length factor
𝒌 = 𝟏. 𝟎 for pinned compression member
𝒌 = 𝟎. 𝟕𝟎 for fixed-pinned compression member
𝒌 = 𝟎. 𝟓𝟎 for both ends fixed against rotation and translation

12. COMPRESSION MEMBERS

13. COMPRESSION MEMBERS
AISC Requirements
The nominal compressive strength is:
𝑷𝒏 = 𝑭𝒄𝒓𝑨𝒈
For LRFD,
𝑷𝒖 ≤ 𝝓𝒄𝑷𝒏
where: 𝑃𝑢 = sum of the factored loads
𝝓𝒄 = resistance factor for compression = 0.90
𝝓𝒄𝑃𝑛 = design compressive strength

14. COMPRESSION MEMBERS
AISC Requirements
For ASD,
𝑷𝒂 ≤
𝑷𝒏
𝛀𝒄
where: 𝑃𝑎 = sum of the service loads
𝛺𝑐= safety factor for compression = 1.67
𝑃𝑛/𝛺𝑐= allowable compressive strength

15. COMPRESSION MEMBERS
AISC Requirements
If an allowable stress formulation is used,
𝒇𝒂 ≤ 𝑭𝒂
where: 𝑓𝑎 = computed axial compressive stress
𝐹𝑎 = allowable axial compressive stress

16. COMPRESSION MEMBERS
Values for full-member increments of 𝑘𝐿/𝑟 for A992 and A36 steel, derived from
the AISC specification formulas, are given in Table 10.1

17. SAMPLE PROBLEM 2
A 𝑊12 × 53 shape of A992 steel is used as a column with an unbraced length
of 16 ft. Compute the maximum factored load using the AISC table. Use 𝐹𝑦 = 50
kips
For 𝑊12 × 53 :
𝑟𝑥 = 5.23 in.
𝑟𝑦 = 2.48 in.
Area, 𝐴 = 15.6 in2
Ans. 𝑷𝒖 = 455 kips

18. SAMPLE PROBLEM 2
Solution:
𝑘𝐿
𝑟𝑚𝑖𝑛
=
1.0 × 16 × 12
2.48
= 77.42
It is usually considered acceptable to round the slenderness ratio off to the nearest whole
number. Thus, with 𝑘𝐿/𝑟 = 77 and with 𝐹𝑦= 50 kips, the critical stress 𝐹𝑐 is 32.4 kips
𝑃𝑢 = 𝜙𝑐𝐹𝑐𝐴 = 0.90 × 32.4 × 15.6 = 𝟒𝟓𝟒. 𝟗𝟎 𝐤𝐢𝐩𝐬

19. SAMPLE PROBLEM 3
A column is to be designed at the location of an exterior wall. The column is
laterally restrained but rotation free at the top and bottom in both directions (on
both 𝑥 and 𝑦 axes). With respect to the 𝑥 axis, the column is laterally unbraced
for its full height. However, the existence of the horizontal framing in the wall
plane provides lateral bracing with respect to the 𝑦 axis of the section; thus, the
buckling of the column in this direction takes the form shown below. If the
column is a 𝑊12 × 53 of A992 steel, 𝐿1 is 30 ft and 𝐿2 is 18 ft, what is the
maximum factored compression load?
Ans. 𝑷𝒖 = 403 kips

20. SAMPLE PROBLEM 3
Solution:
For 𝑊12 × 53 :
𝑟𝑥 = 5.23 in.
𝑟𝑦 = 2.48 in.
𝐴 = 15.6 in2
𝑥-axis:
𝑘𝐿𝑥
𝑟𝑥
=
1 × 30 × 12
5.23
= 68.83 ≈ 69
𝑦-axis:
𝑘𝐿𝑦
𝑟𝑦
=
1 × 18 × 12
2.48
= 87.10 ≈ 87
It is usually considered acceptable to round the slenderness ratio off to the nearest whole
number. Thus, with 𝑘𝐿/𝑟 = 77 and with 𝐹𝑦= 50 kips, the critical stress 𝐹𝑐 is 32.4 kips
𝑃𝑢 = 𝜙𝑐𝐹𝑐𝐴 = 0.90 × 28.7 × 15.6 = 𝟒𝟎𝟐. 𝟗𝟓 𝐤𝐢𝐩𝐬

21. COMPRESSION MEMBERS
AISC Requirements
The Euler stress equation is
𝑭𝒆 =
𝑷𝒆
𝑨
=
𝝅𝟐𝑬
(𝒌𝑳/𝒓)𝟐
With a slight modification, this expression will be used for the critical stress
in the elastic range. To obtain the critical stress for elastic columns, the Euler
stress is reduced as follows to account for the effects of initial crookedness:
𝑭𝒄𝒓 = 𝟎. 𝟖𝟕𝟕𝑭𝒆

22. COMPRESSION MEMBERS
AISC Requirements
For inelastic columns, the tangent modulus equation is replaced by the
exponential equation
𝑭𝒄𝒓 = 𝟎. 𝟔𝟓𝟖
𝑭𝒚
𝑭𝒆 𝑭𝒚

23. COMPRESSION MEMBERS
AISC Requirements
𝐹𝑐𝑟
𝑘𝐿
𝑟
𝐹𝑦
𝑭𝒄𝒓 = 𝟎. 𝟔𝟓𝟖
𝑭𝒚
𝑭𝒆 𝑭𝒚
Inelastic buckling
𝑭𝒄𝒓 = 𝟎. 𝟖𝟕𝟕𝑭𝒆
Elastic buckling
4.71 𝐸/𝐹𝑦

24. COMPRESSION MEMBERS
AISC Requirements
To summarize,
When
𝑘𝐿
𝑟
≤ 4.71
𝐸
𝐹
𝑦
𝑭𝒄𝒓 = 𝟎. 𝟔𝟓𝟖
𝑭𝒚
𝑭𝒆 𝑭𝒚
When
𝑘𝐿
𝑟
> 4.71
𝐸
𝐹
𝑦
𝑭𝒄𝒓 = 𝟎. 𝟖𝟕𝟕𝑭𝒆

25. SAMPLE PROBLEM 4
A W14 x 74 of A992 steel has a length of 20 feet and pinned ends. Compute
the design compressive strength for LRFD and the allowable compressive
strength for ASD. Use 𝐴𝑔= 21.8 in2, 𝐹𝑦 = 50 ksi and 𝐸 = 29000 ksi
Ans. 𝝓𝒄𝑷𝒏 = 495 kips
𝑷𝒏/𝜴𝒄 = 329 kips

26. SAMPLE PROBLEM 4
Solution:
Maximum
𝑘𝐿
𝑟
=
𝑘𝐿
𝑟𝑦
=
1.0 20 × 12
2.48
= 96.77
4.71
𝐸
𝐹𝑦
= 4.71
29 000
50
= 113.43
Since
𝑘𝐿
𝑟
< 4.71
𝐸
𝐹𝑦
, the column will undergo inelastic buckling 𝐹𝑐𝑟 = 0.658
𝐹𝑦
𝐹𝑒 𝐹𝑦
𝐹𝑒 =
𝜋2𝐸
𝑘𝐿/𝑟 2 =
𝜋2
(29000)
96.77 2
= 30.56 ksi
𝐹𝑐𝑟 = 0.658
𝐹𝑦
𝐹𝑒 𝐹𝑦 = 0.658
50
30.56 × 50 = 25.21 ksi
Nominal strength: 𝑃𝑛 = 𝐹𝑐𝑟𝐴𝑔 = 25.21 21.8 = 549.58 ksi

27. SAMPLE PROBLEM 4
Solution:
Nominal strength: 𝑃𝑛 = 𝐹𝑐𝑟𝐴𝑔 = 25.21 21.8 = 549.58 ksi
Design strength:
𝜙𝑐𝑃𝑛 = 0.90 549.58 = 𝟒𝟗𝟒. 𝟔𝟐 𝐤𝐬𝐢
Allowable strength:
𝑃𝑛
𝛺𝑐
=
549.58
1.67
= 𝟑𝟐𝟗. 𝟎𝟗 𝐤𝐬𝐢