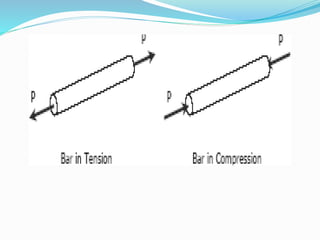
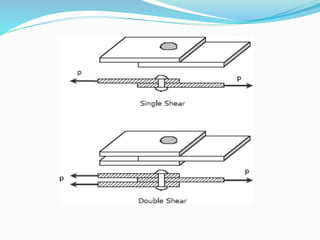
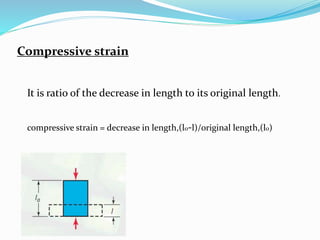
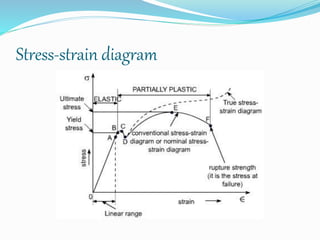
The document discusses different types of stresses and strains experienced by materials. It defines normal stress as stress perpendicular to the resisting area, with tensile and compressive stresses elongating and shortening materials. Combined stress includes shear and torsional stresses from parallel forces. Strain is defined as the change in dimension due to an applied force. The stress-strain diagram is then explained, showing the material's behavior from the proportional limit through yielding and strain hardening until ultimate failure. Key points on the curve include the proportionality limit, elastic limit, yield points, and ultimate stress.

1. 1

3. PARTICIPANTS NAME
 SATYAM SINGH (11SETME252)
 SAYANTAN DAS (11SETEM480)
 VIBHAS KUMAR (11SETME165)
 SUMIT RAJ (11SETME363)
 VISHAL BASNET (11SETME411)

4. Stress
Simple stresses are expressed as the ratio of the applied
force divided by the resisting area or
σ = Force / Area.
There are two types of simple stress namely;
normal stress,
combined stress

5. Normal Stress
The resisting area is perpendicular to the applied force, thus normal. There are
two types of normal stresses;
Tensile stress
Compressive stress.
Tensile stress applied to bar tends the bar to elongate
while compressive stress tend to shorten the bar.
where P is the applied normal load in Newton and A is the area in mm2.

7. Combined Stress
In combined stress there are two types of stress
 Shear stress
Tortional stress

8. Shear Stress
Forces parallel to the area resisting the force cause
shearing stress.
It differs to tensile and compressive stresses, which are
caused by forces perpendicular to the area on which they
act.
Shearing stress is also known as tangential stress.
where V is the resultant shearing force which passes which
passes through the centroid of the area A being sheared.

10. Tortional stress
The stresses and deformations induced in a circular shaft by a
twisting moment.

11. Strain
Also known as unit deformation, strain is the ratio of the change
in dimension caused by the applied force, to the original
dimension.
where δ is the deformation and L is the original length, thus ε is
dimensionless.

12. Types of strain:
Tensile strain
Compressive strain
Shear strain
Volumetric strain

13. Tensile strain
It is the ratio of the increase in length to its original length.
Tensile strain = increase in length,(l-l0)/original length,(l0)

14. Compressive strain
It is ratio of the decrease in length to its original length.
compressive strain = decrease in length,(l0-l)/original length,(l0)

15. Shear strain
We can define shear strain exactly the way we do longitudinal strain: the ratio of
deformation to original dimensions.
tan

16. Volumetric strain
Volumetric strain of a deformed body is defined as the ratio of the change in volume of the
body to the deformation to its original volume.
volumetric strain = change in volume/original volume

17. Stress-strain diagram

18. The curve starts from the origin ‘O’ showing thereby that there
is no initial stress or strain in the test specimen.
Up to point ‘A’ Hooke’s law is obeyed and stress is proportional
to strain therefore ‘OA’ is straight line and point ‘A’ is called
the proportionality limit stress.
The portion between ‘AB’ is not a straight line, but up to point
‘B’, the material remains elastic.

19. The point ‘B’ is called the elastic limit point and the stress
corresponding to that is called the elastic limit stress.
Beyond the point ‘B’, the material goes to plastic stage until the
upper yield point ‘C’ is reached.
At this point the cross-sectional area of the material starts
decreasing and the stress decreases to a lower value to a point ‘D’,
called the lower yield point.
Corresponding to point ‘C’, the stress is known as upper yield
point stress.

20. At point ‘D’ the specimen elongates by a considerable amount
without any increase in stress and up to point ‘E’.
The portion ‘DE’ is called the yielding of the material at
constant stress.
From point ‘E’ onwards , the strain hardening phenomena
becomes pre-dominant and the strength of the material
increases thereby requiring more stress for deformation,
until point ‘F’ is reached.

21. Point ‘F’ is called the ultimate point and the stress
corresponding to this point is called the ultimate stress.
It is the maximum stress to which the material can be
subjected in a simple tensile test.
At point ‘F’ the necking of the material begins and the cross-sectional
area starts decreasing at a rapid rate.
Due to this local necking the stress in the material goes on
decreasing inspite of the fact that actual stress intensity goes
on increasing.

22. Ultimately the specimen breaks at point ‘G’, known as the
breaking point, and the corresponding stress is called the
normal breaking stress bared up to original area of cross-section.

23. Thanks for your kind attention….