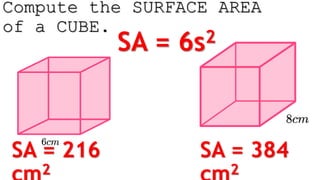
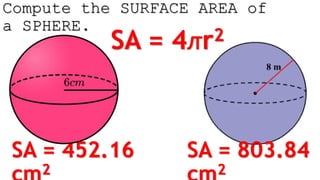
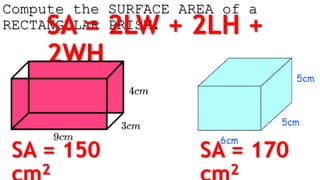
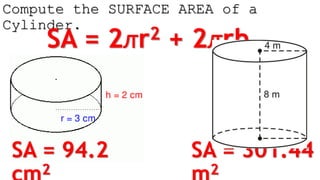
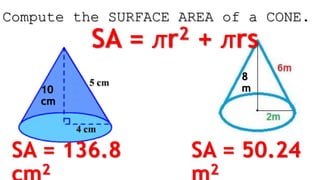
The document outlines methods for calculating the surface areas of various three-dimensional shapes including cubes, prisms, pyramids, cylinders, cones, and spheres. It provides specific formulas for each shape, illustrated with examples such as wrapping a gift and calculating the surface area for items like a pool and a cylindrical tank. Additionally, it details how much surface cover (such as gift wrap or glitter) is required for these objects based on their dimensions.

2. Learning Target:
b. Find the surface area of cube,
prism, pyramid, cylinder, cone,
and sphere.
a. Derive a formula for finding the
surface area of cube, prism, pyramid,
cylinder, cone and sphere; and

3. How do I find
out how much
gift-wrap I need
to buy for this
box?
You need to get
the surface area
of the box.

4.  is the total area of
the surface of a three-
dimensional object.

5. Ana wraps her gift for Elsa. The
measure of the edge of the cube is 10
inches. She does not have extra
paper, so she does not overlap any of
the edges. How much paper was used
to cover Ana’s gift?
Formula:
Cube
SA =
6s2
=
6
x 10
in
2
= 6 x 100
in2
= 600 in2

6. Compute the SURFACE AREA
of a CUBE.
SA = 6s2
SA = 216
2
SA = 384
2

7. A Christmas ball has a radius of 11
cm. If its surface area is to be
filled up with glitters, how much
area will be covered with glitters?
Formula:
Sphere
SA = 4ꙥr2
= 4ꙥx 11 cm2
= 4ꙥ x 121 cm2
= 1519.76 cm2
= 4 x 3.14 x 121 cm2

8. Compute the SURFACE AREA of
a SPHERE.
SA = 4ꙥr2
SA = 452.16
2
SA = 803.84
2

9. Mark has a pool filled with water. The
pool is 10 m long, 8 m wide, and 4 m
deep. Find the surface area of the
pool.
Formula:
Rectangular
Prism
SA = 2LW + 2LH +
2WH
= 2(10 x 8) + 2(10 x 4) +
2 (8 x 4)
= 2 (80) + 2 (40) + 2
(32)
= 304 m2
= 160 + 80 + 64

10. Compute the SURFACE AREA of a
RECTANGULAR PRISM.
SA = 2LW + 2LH +
2WH
SA = 150
2
SA = 170
2

11. Our cylindrical tank has a radius
of 5 ft and height of 10 ft. How
much paint is needed to paint its
surface?
Formula:
Cylinder
SA = 2ꙥr2 +
2ꙥrh
= 2(3.14 x 52) + 2(3.14 x 5 x
10)
= 2(3.14 x 25) + 2(3.14 x 50)
= 2(78.5) + 2(157)
= 157 + 314
= 471 ft2

12. Compute the SURFACE AREA of a
Cylinder.
SA = 2ꙥr2 + 2ꙥrh
SA = 94.2
2
SA = 301.44
2

13. A cone has a radius of 3 cm,
height of 4 cm and the slant
measures 5 cm. Find the total
surface area of the cone.
Formula:
Cone
SA = ꙥr2 + ꙥrs
= 3.14 x 32 + 3.14 x 3 x 5
= 3.14 x 9 + 3.14 x 15)
= 28.26 + 47.1
= 75.36 cm2

14. Compute the SURFACE AREA of a CONE.
SA = ꙥr2 + ꙥrs
SA = 136.8
2
SA = 50.24
2
10
cm
8
m