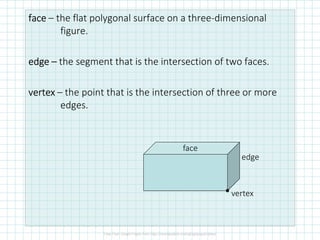
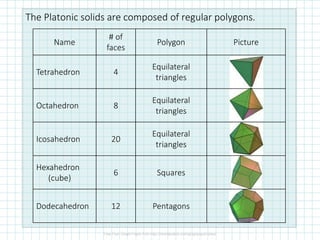
Solid geometry involves classifying and analyzing three-dimensional shapes. Key concepts include polyhedra composed of polygons, prisms with two parallel congruent bases, pyramids with a polygonal base meeting at a common vertex, and using nets which can be folded to form three-dimensional shapes. Formulas relate the number of vertices, edges and faces of polyhedra. Surface area calculations involve finding the total area of each face.

1. Solid Geometry
The student is able to (I can):
• Classify three-dimensional figures according to their
properties
• Associate two-dimensional nets with their three-
dimensional shapes
• Analyze the cross-sections of three-dimensional shapes

2. facefacefaceface – the flat polygonal surface on a three-dimensional
figure.
edgeedgeedgeedge –––– the segment that is the intersection of two faces.
vertexvertexvertexvertex – the point that is the intersection of three or more
edges.
face
edge
vertex•

3. polyhedronpolyhedronpolyhedronpolyhedron – a three-dimensional figure composed of
polygons. (plural polyhedrapolyhedrapolyhedrapolyhedra)
prismprismprismprism – two parallel congruent polygon bases connected by
faces that are parallelograms.
cylindercylindercylindercylinder – two parallel congruent circular bases and a curved
surface that connects the bases.

4. pyramidpyramidpyramidpyramid – a polygonal base with triangular faces that meet at
a common vertex.
coneconeconecone – a circular base and a curved surface that connects the
base to a vertex.

5. rightrightrightright prismprismprismprism – a prism whose faces are all rectangles. (Assume
a prism is a right prism unless noted otherwise.)
obliqueobliqueobliqueoblique prismprismprismprism – a prism whose faces are not rectangles.
altitudealtitudealtitudealtitude – a perpendicular segment joining the planes of the
bases (the height).

6. crosscrosscrosscross sectionsectionsectionsection – the intersection of a three-dimensional figure
and a plane.

7. Examples Describe the cross sections:
1.
2.

8. Examples Describe the cross sections:
1.
2.
A hexagon
A triangle

9. A cubecubecubecube is a prism with six square faces. Other prisms and
pyramids are named for the shape of their bases:

10. The Platonic solids are composed of regular polygons.
Name
# of
faces
Polygon Picture
Tetrahedron 4
Equilateral
triangles
Octahedron 8
Equilateral
triangles
Icosahedron 20
Equilateral
triangles
Hexahedron
(cube)
6 Squares
Dodecahedron 12 Pentagons

11. Euler’s Formula
For any polyhedron with V vertices, E edges, and F faces:
V − E + F = 2.
Example: If a given polyhedron has 12 vertices and 18 edges,
how many faces does it have?
− + =
− + =
=
2
12 18 2
8
V E F
F
F

12. netnetnetnet – a diagram of the surfaces of a three-dimensional figure
that can be folded to form the figure.
To identify a figure from a net, look at the number of faces
and the shape of each face.
This is the net of a
cube because it
has six squares.

13. Examples Describe the three-dimensional figure from
the net.
1.
2.
Triangular
Pyramid
Cylinder

14. The surface areasurface areasurface areasurface area is the total area of all faces and curved
surfaces of a three-dimensional figure. The lateral arealateral arealateral arealateral area of a
prism is the sum of the areas of the lateral faces.
Let’s look at a net for a hexagonal prism:

15. If each side of the hexagon is 10 in., what is the area of the
hexagon?
What is the area of each rectanglular face if the height of the
prism is 16 in?
What is the total surface area?

16. If each side of the hexagon is 10 in., what is the area of the
hexagon?
What is the area of each rectanglular face if the height of the
prism is 16 in?
What is the total surface area?
( )
2
210 3
6 6 25 3 150 3 in
4
 
= = 
 
2
150 3 in
2
150 3 in
( )( ) 2
10 16 160 in=
160in2
( ) ( ) 2
2 150 3 6 160 1479.6 in+ ≈

17. If we take the shape below and rotate it about the indicated
axis, we will generate a three-dimensional figure. The type of
figure generated depends on the initial shape andandandand the axis
around which it is rotated.
Thus, rotating the rectangle about the axis has created a
cylinder.