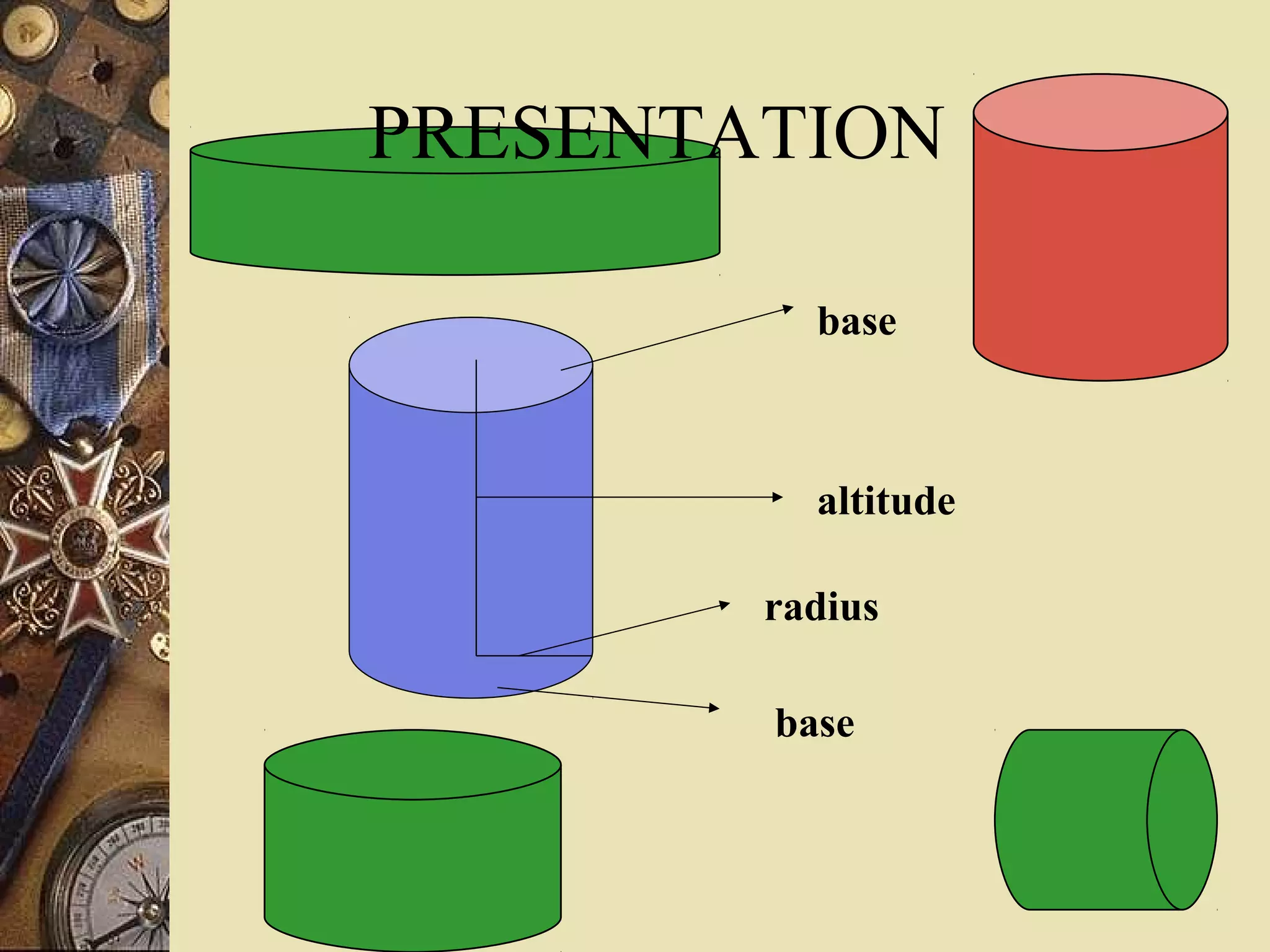
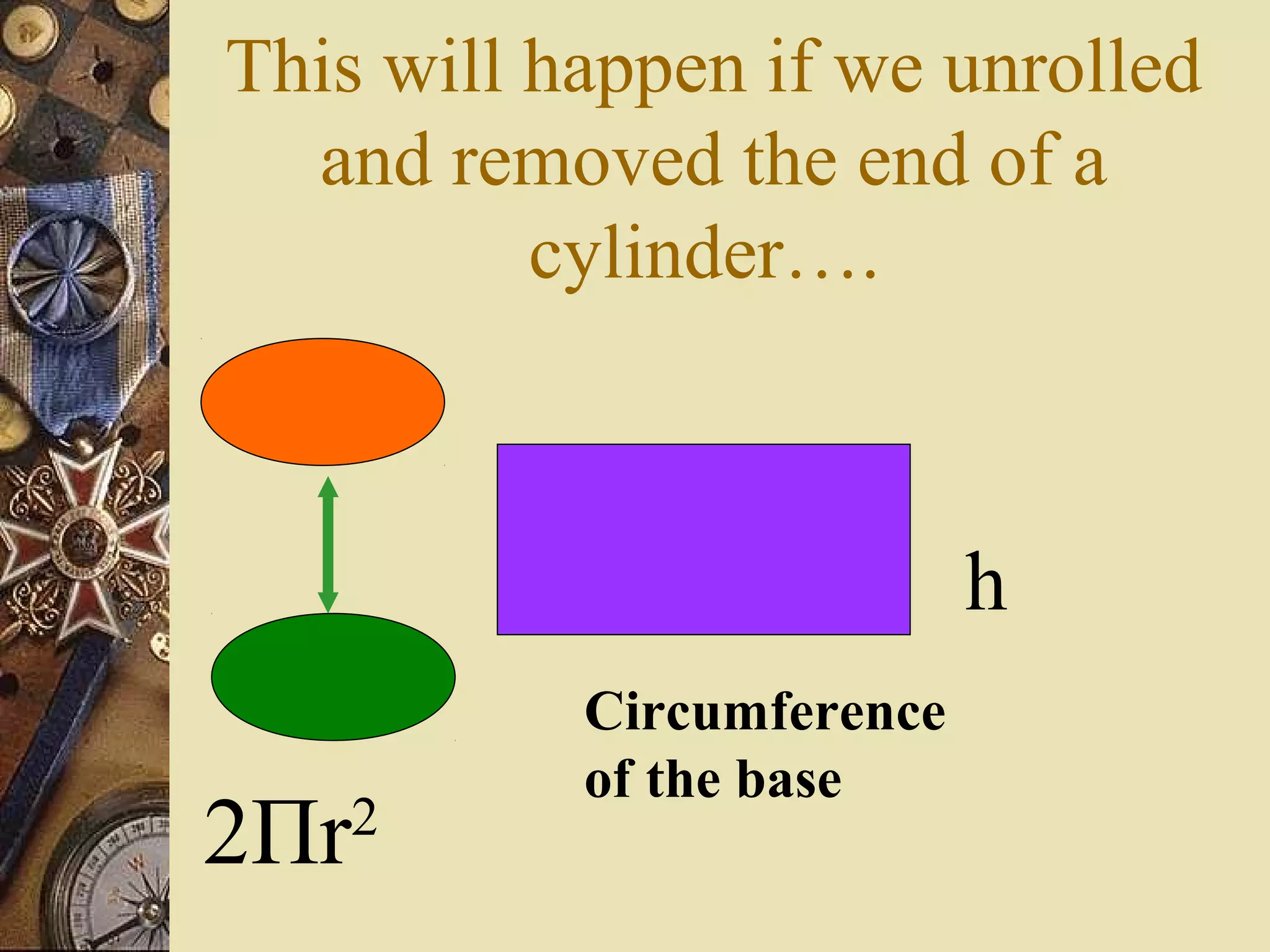
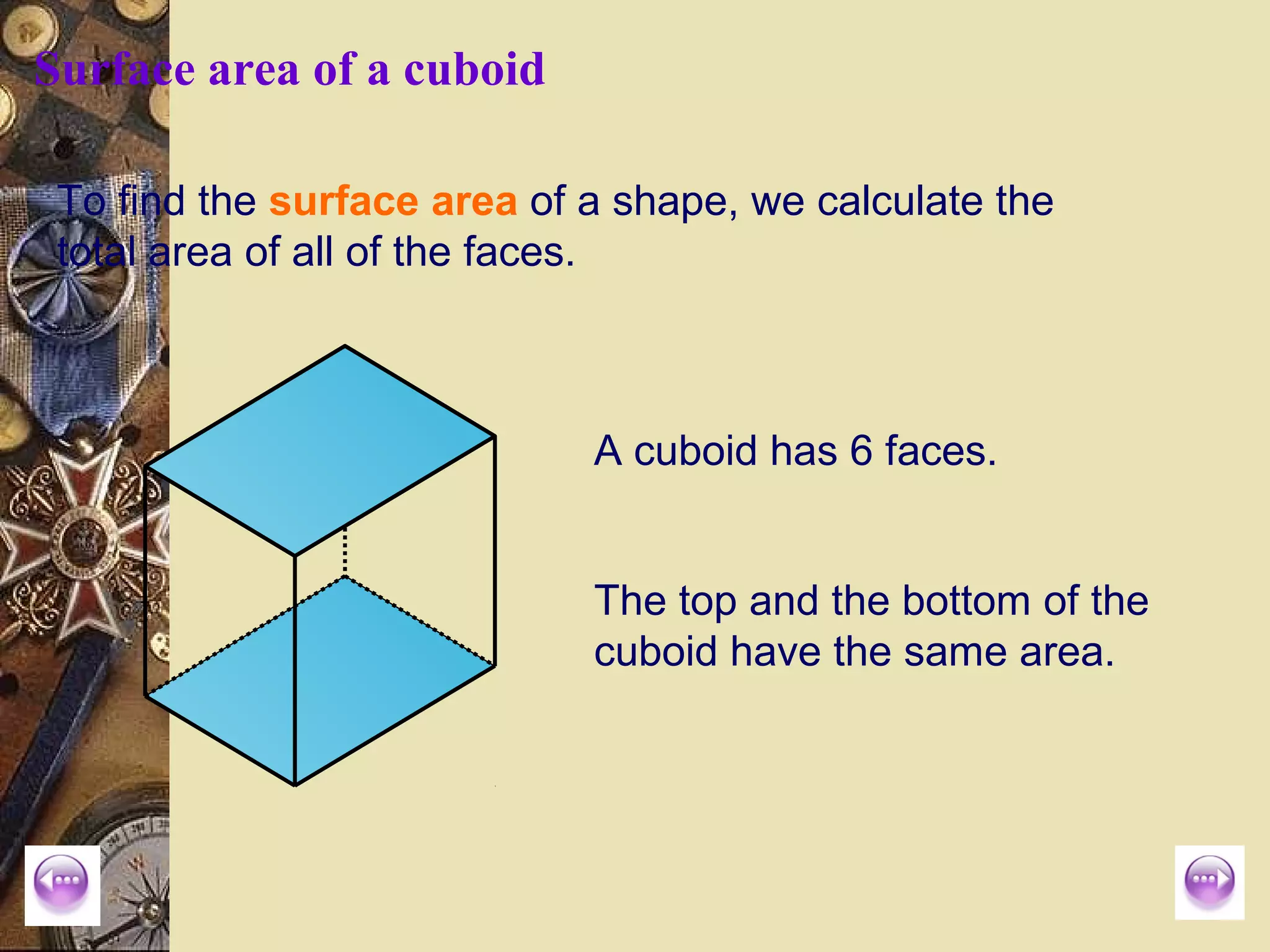
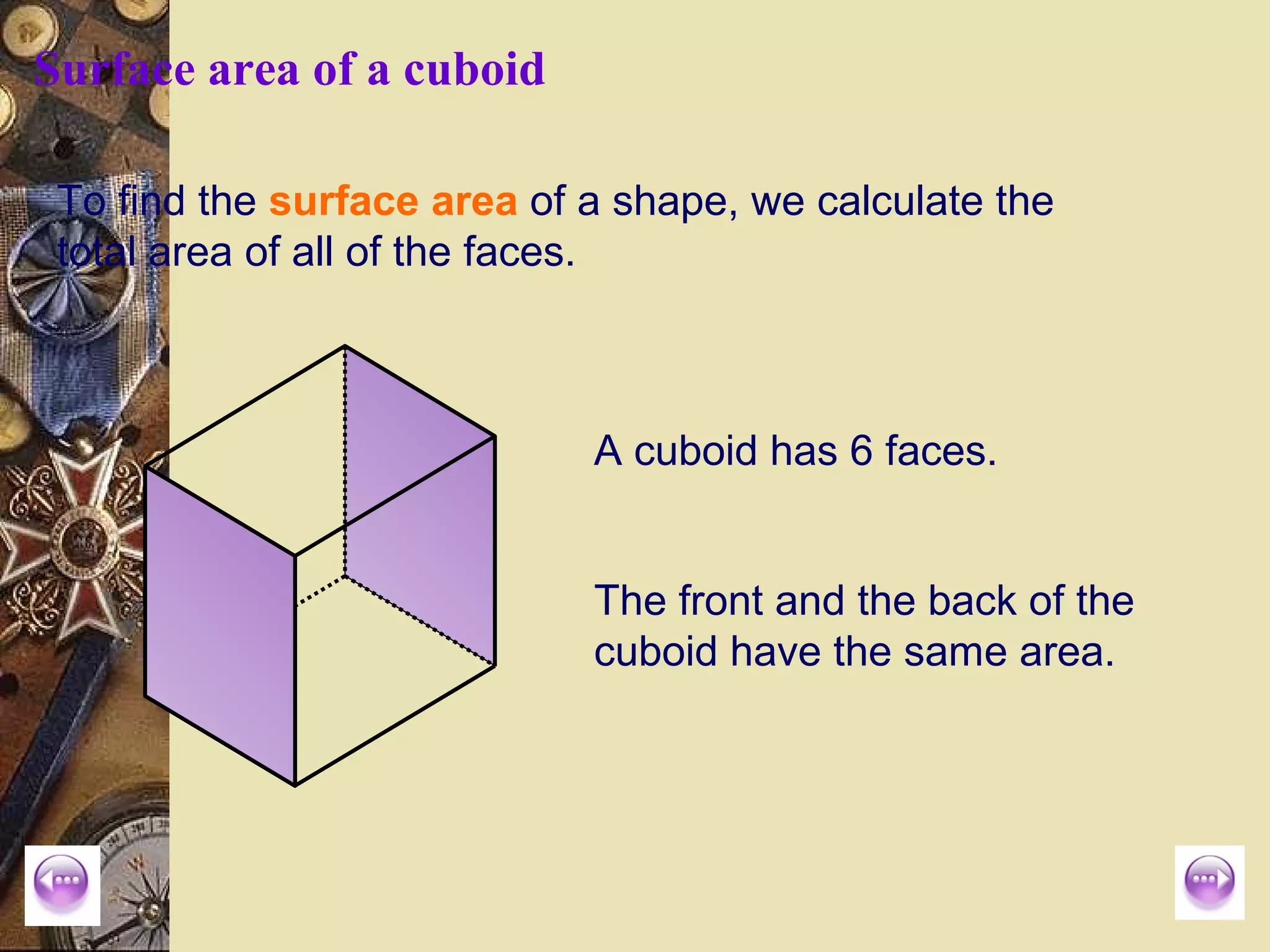
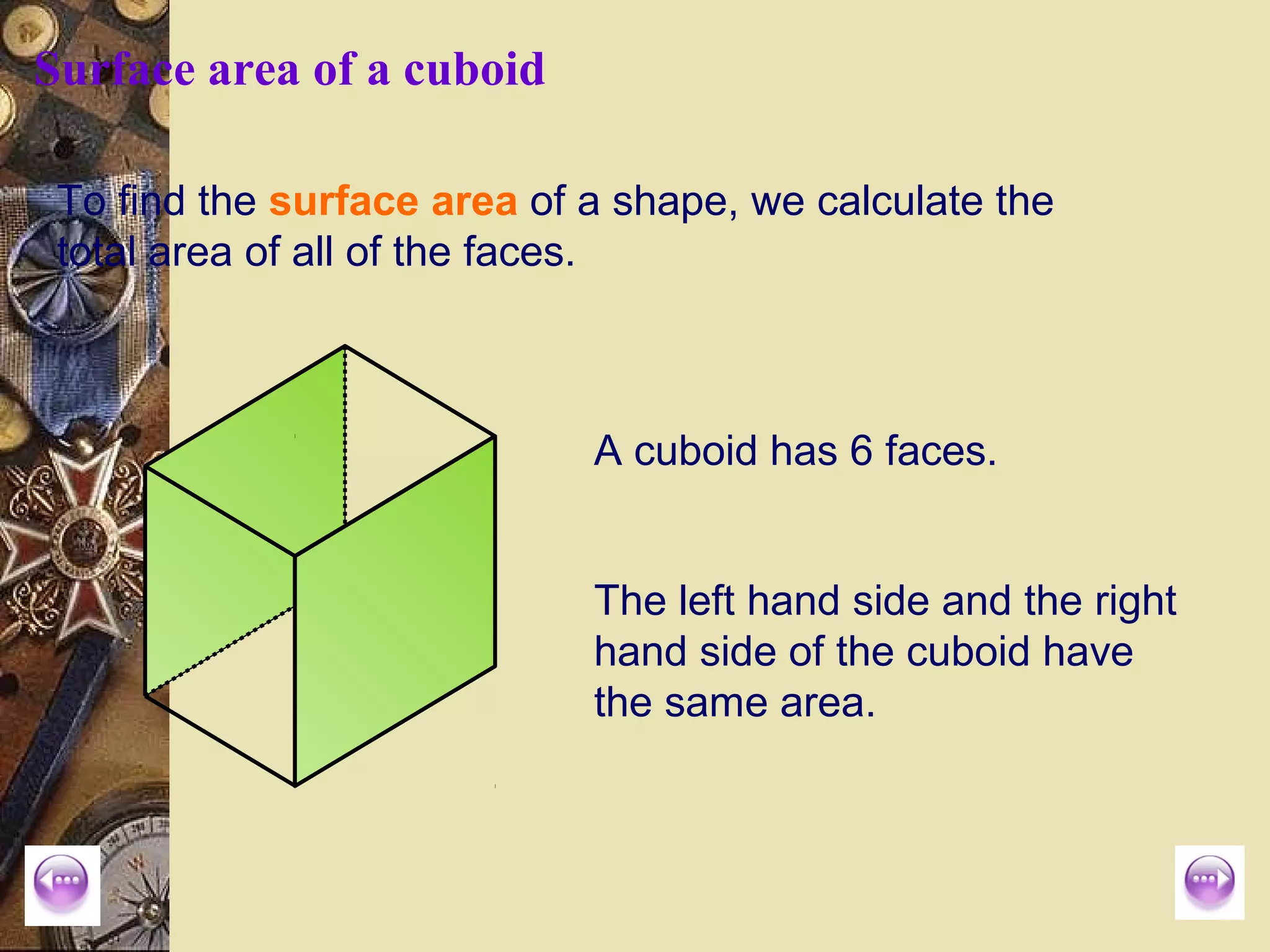
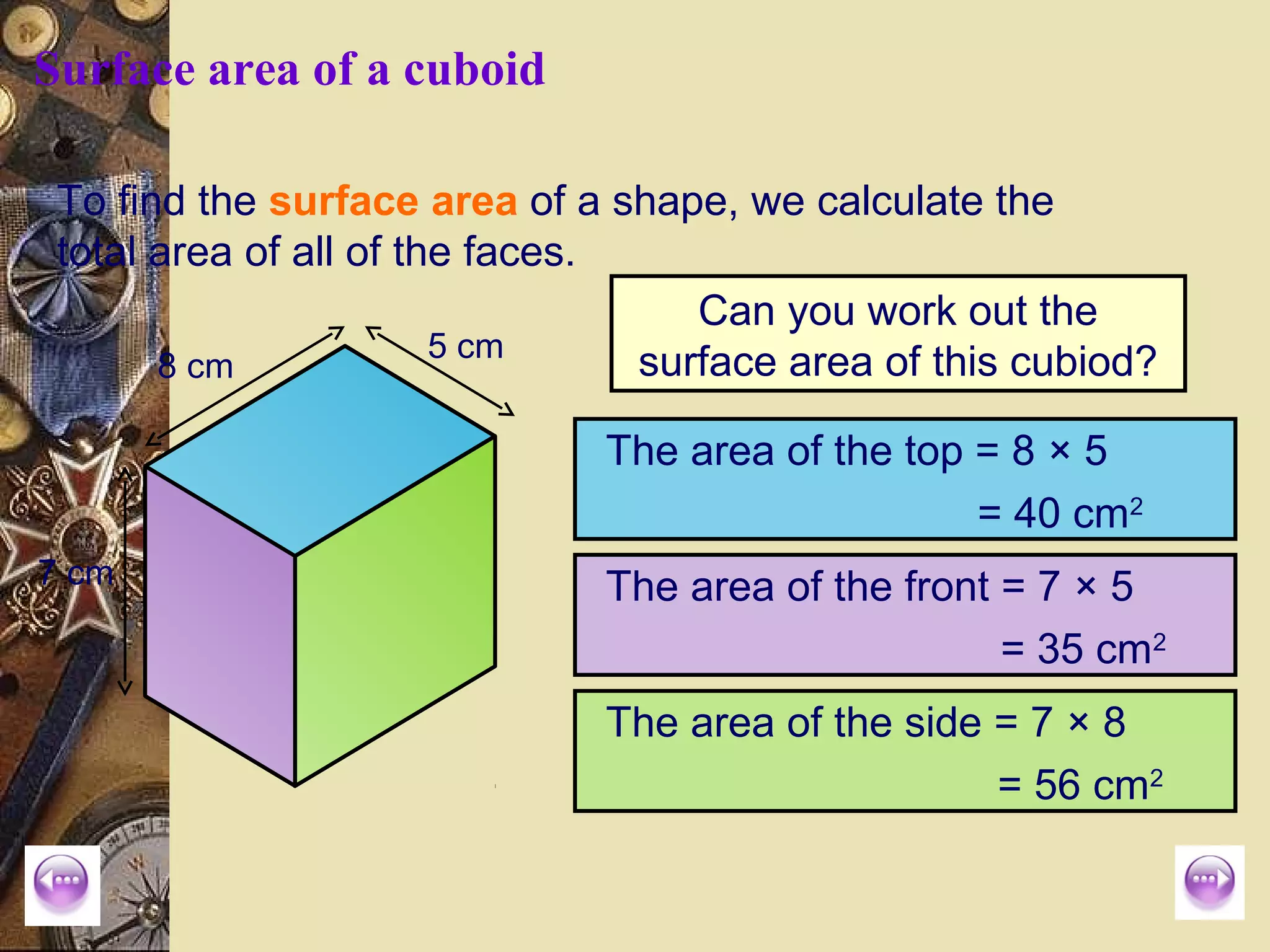
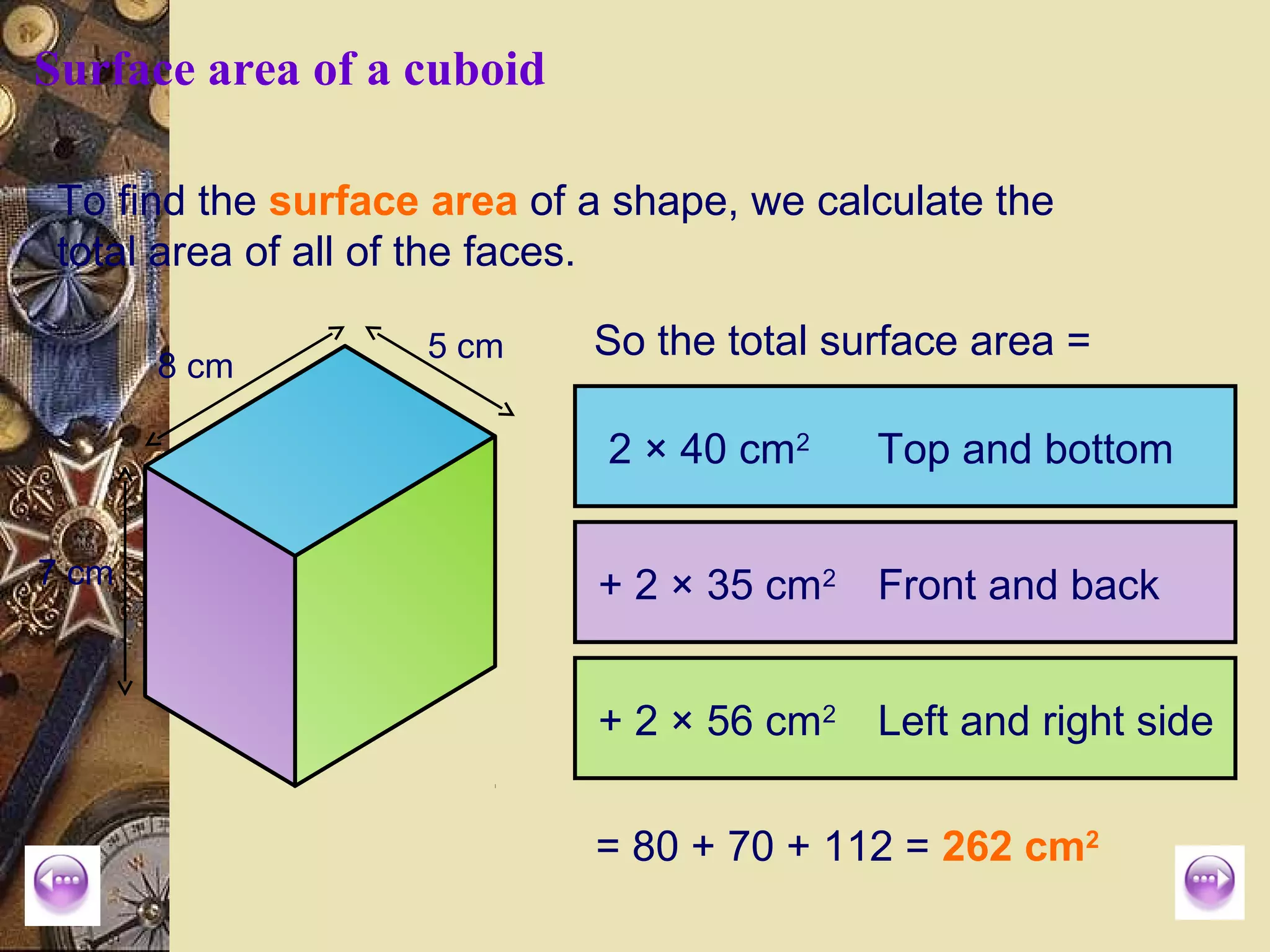
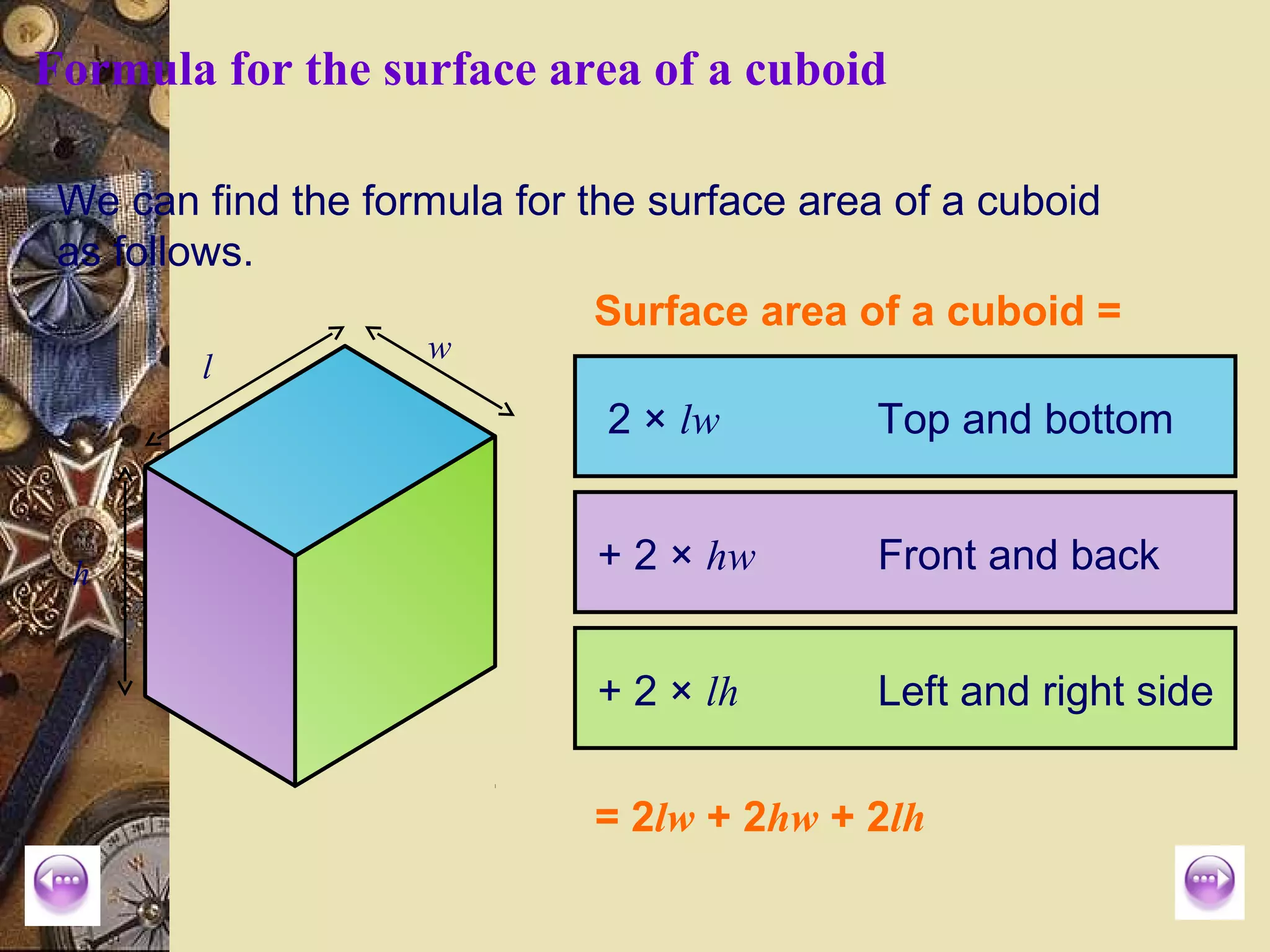
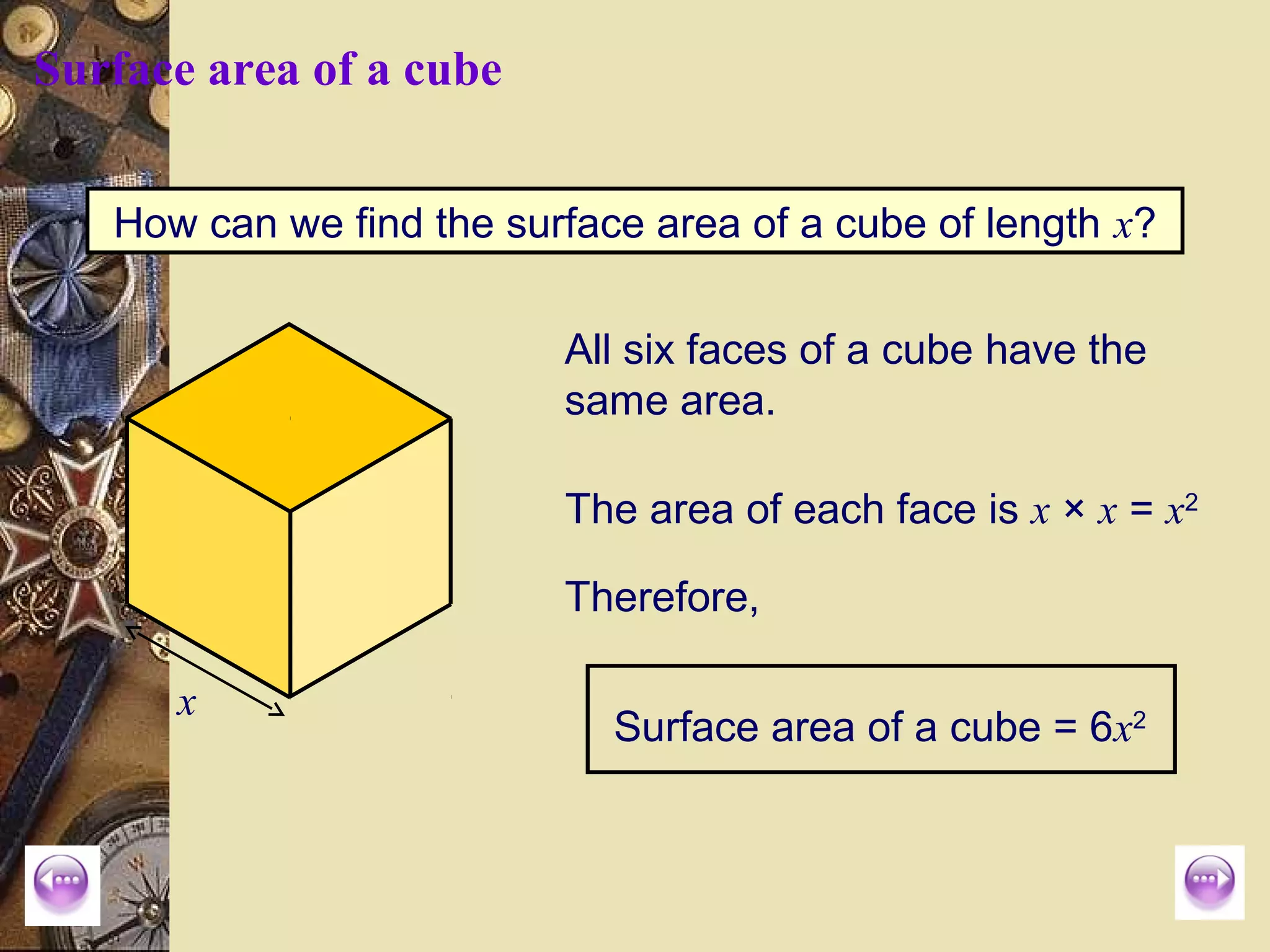
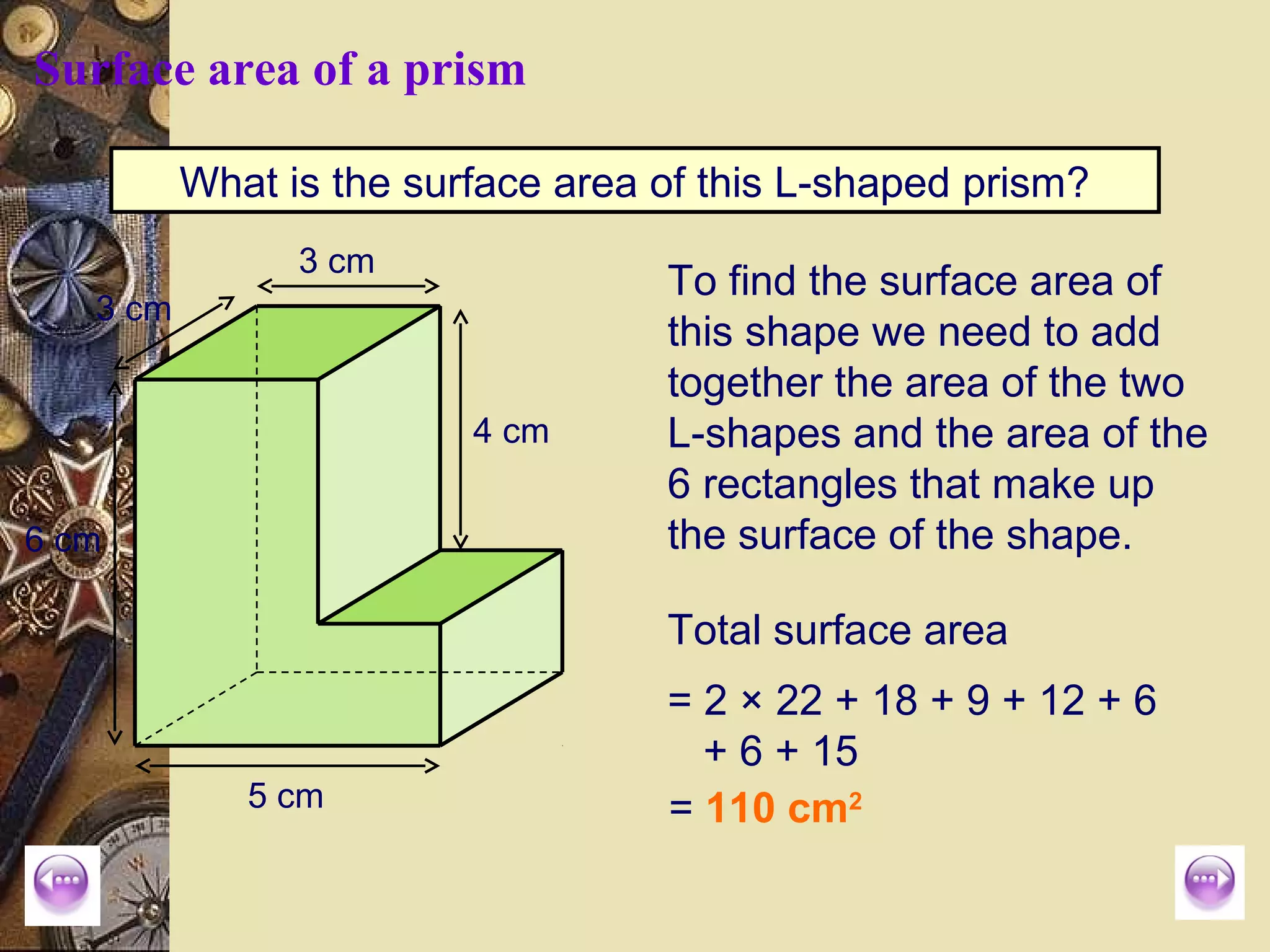
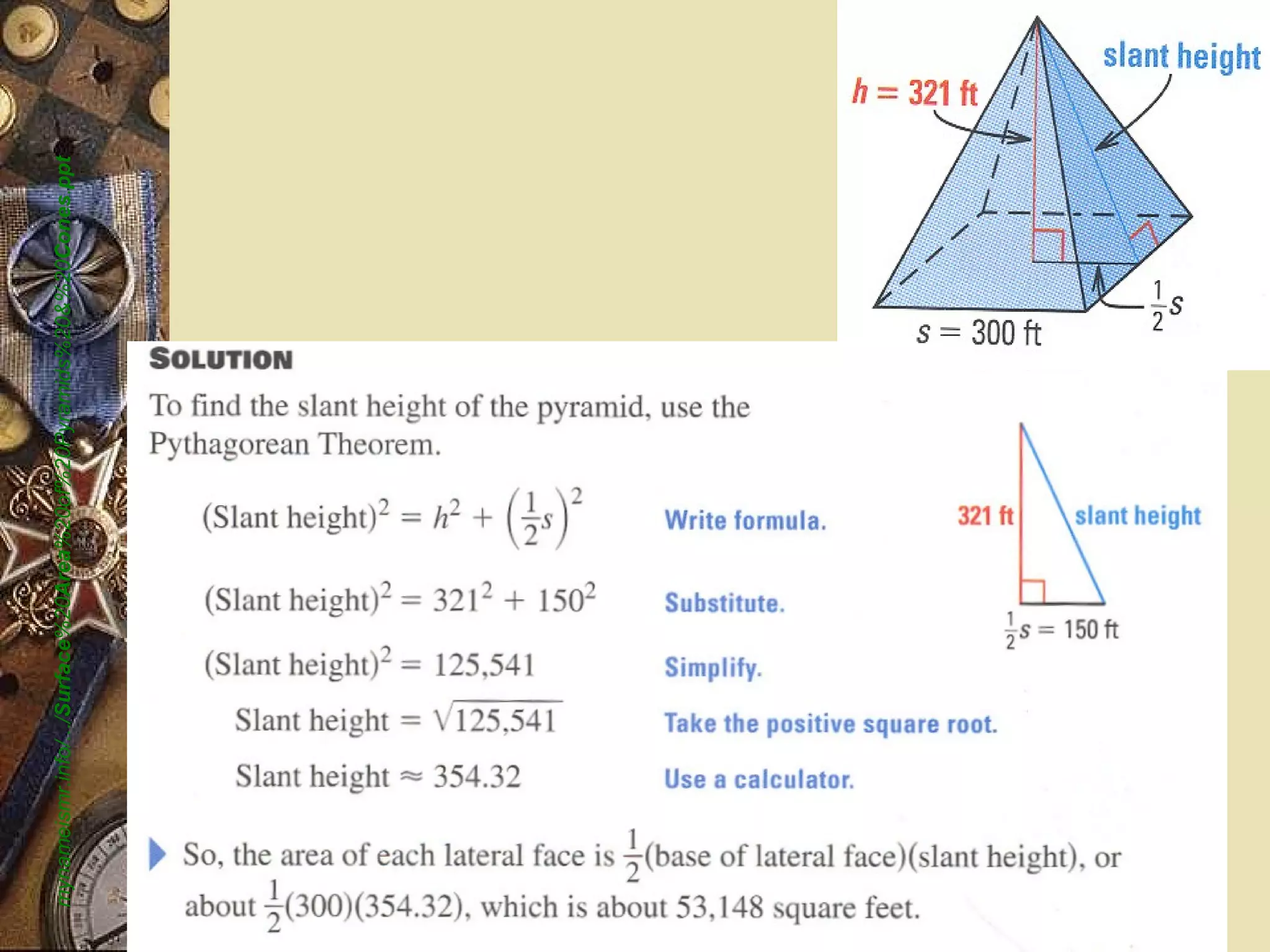
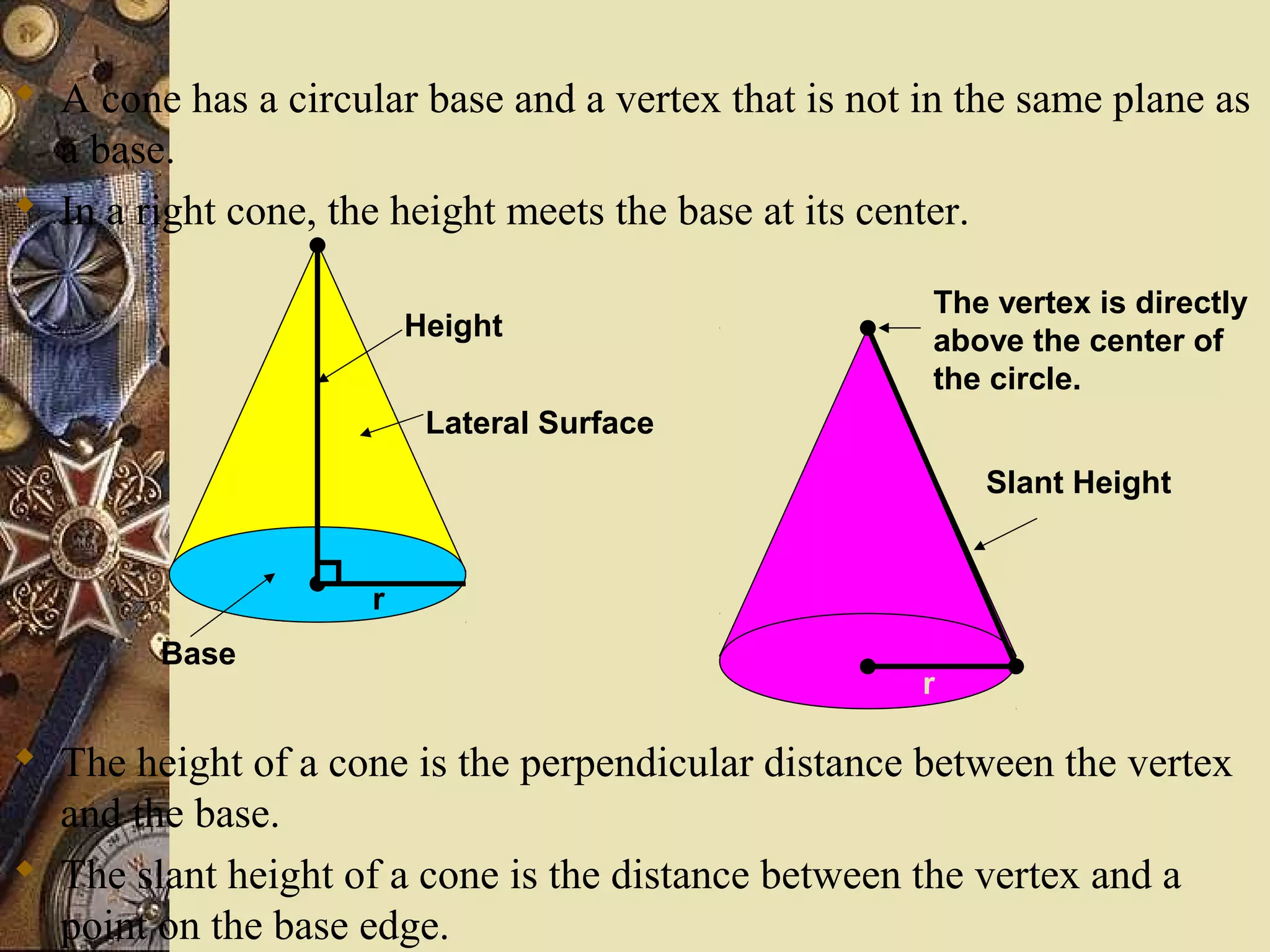
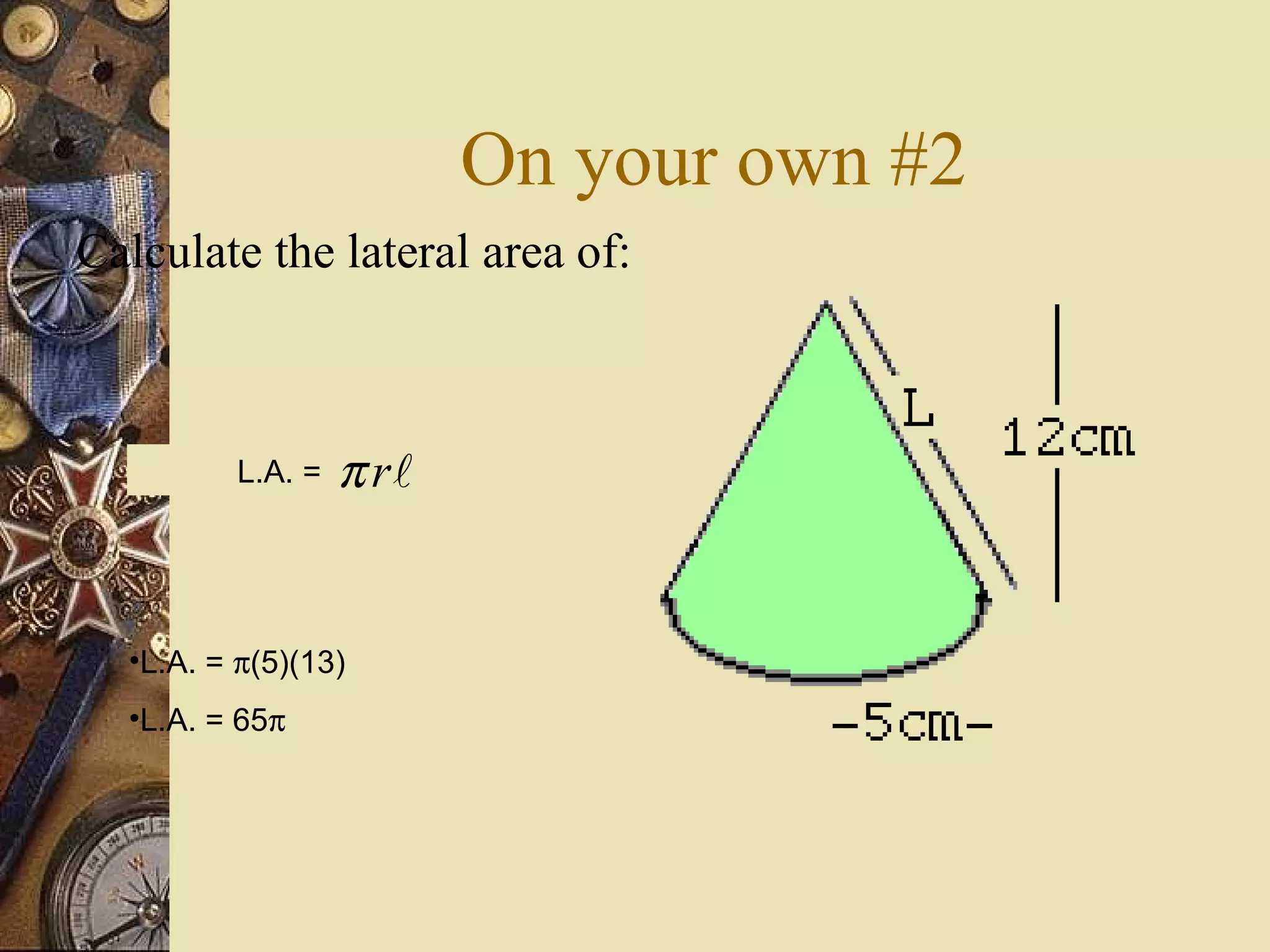
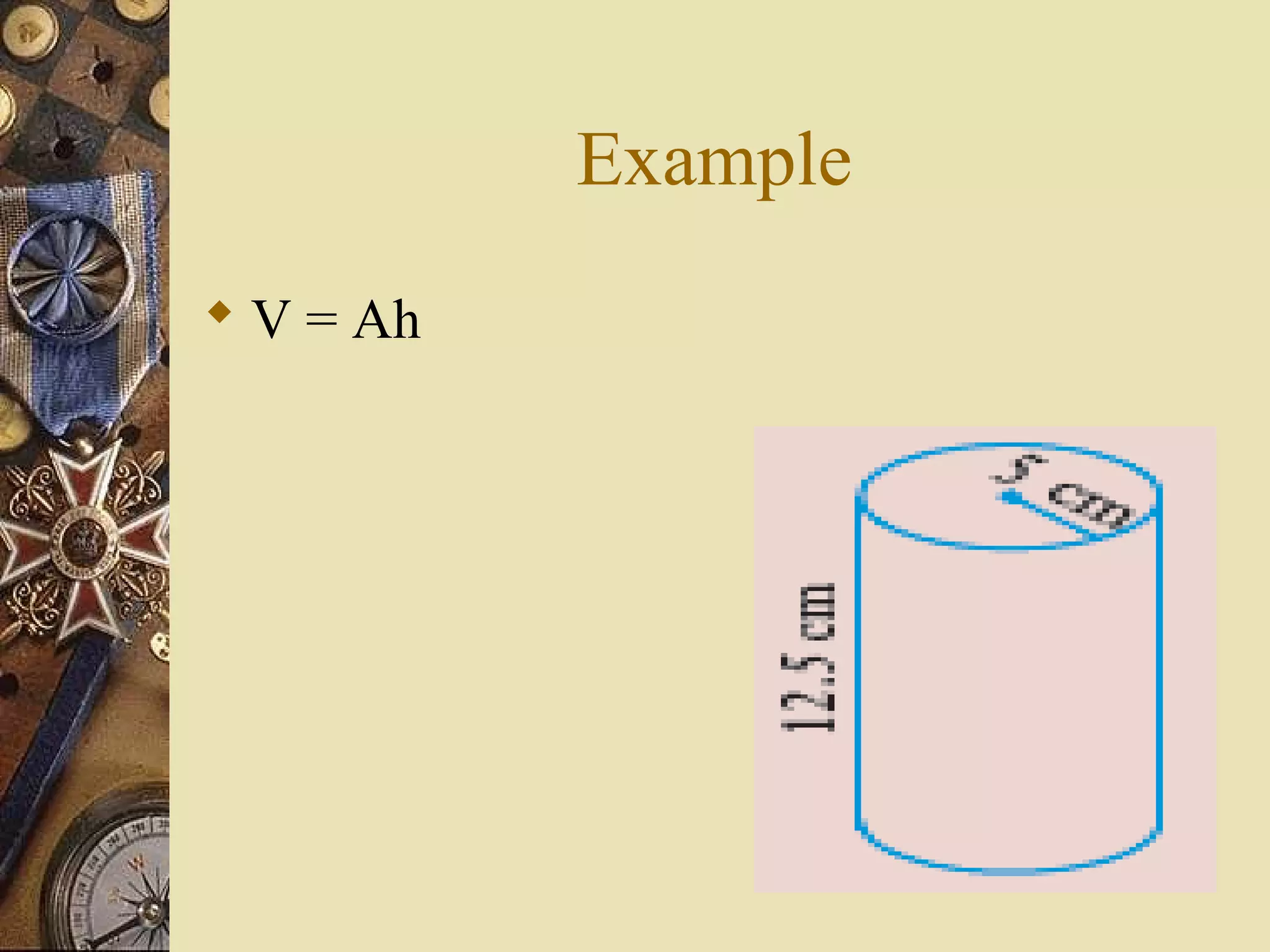
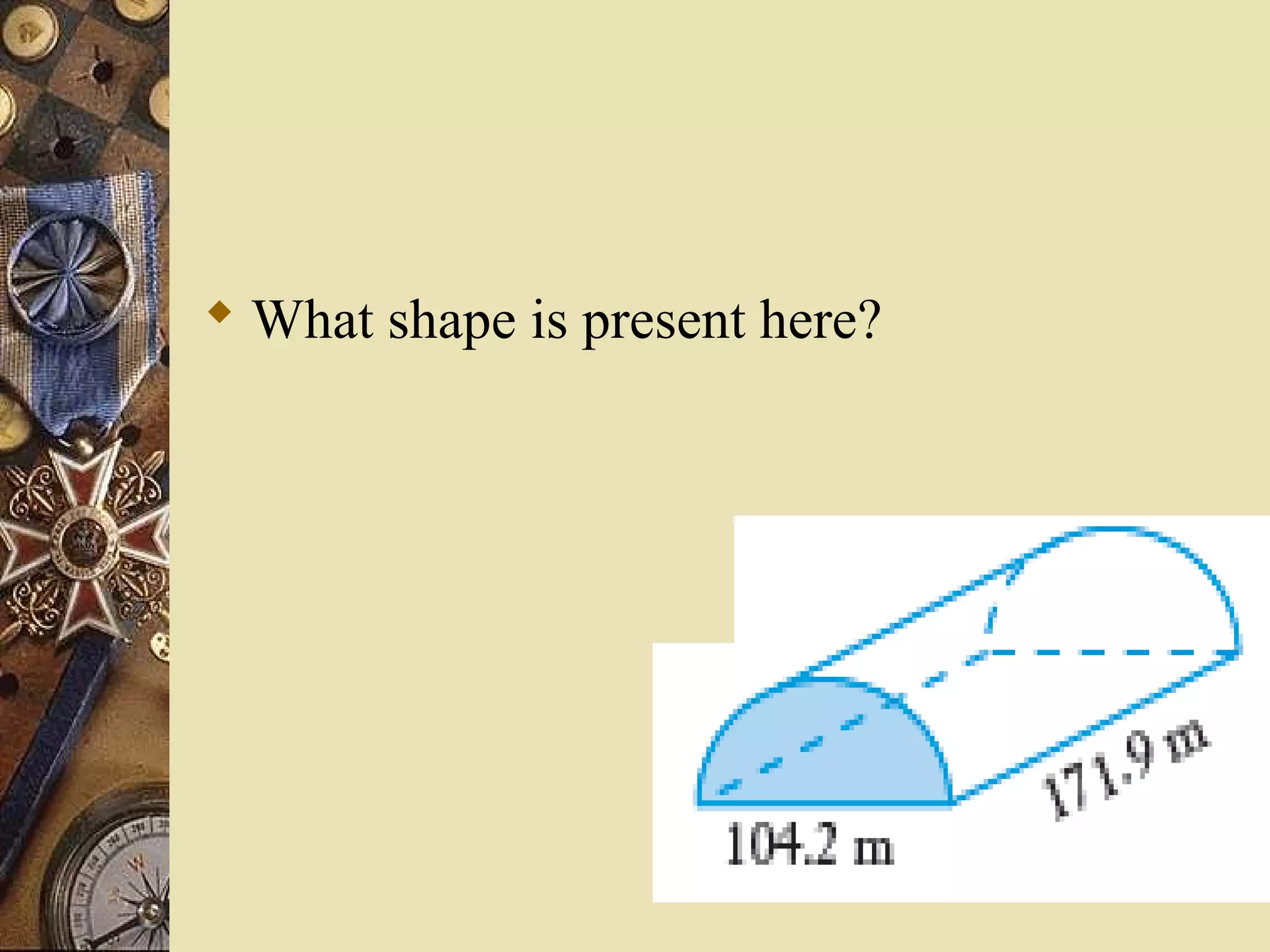
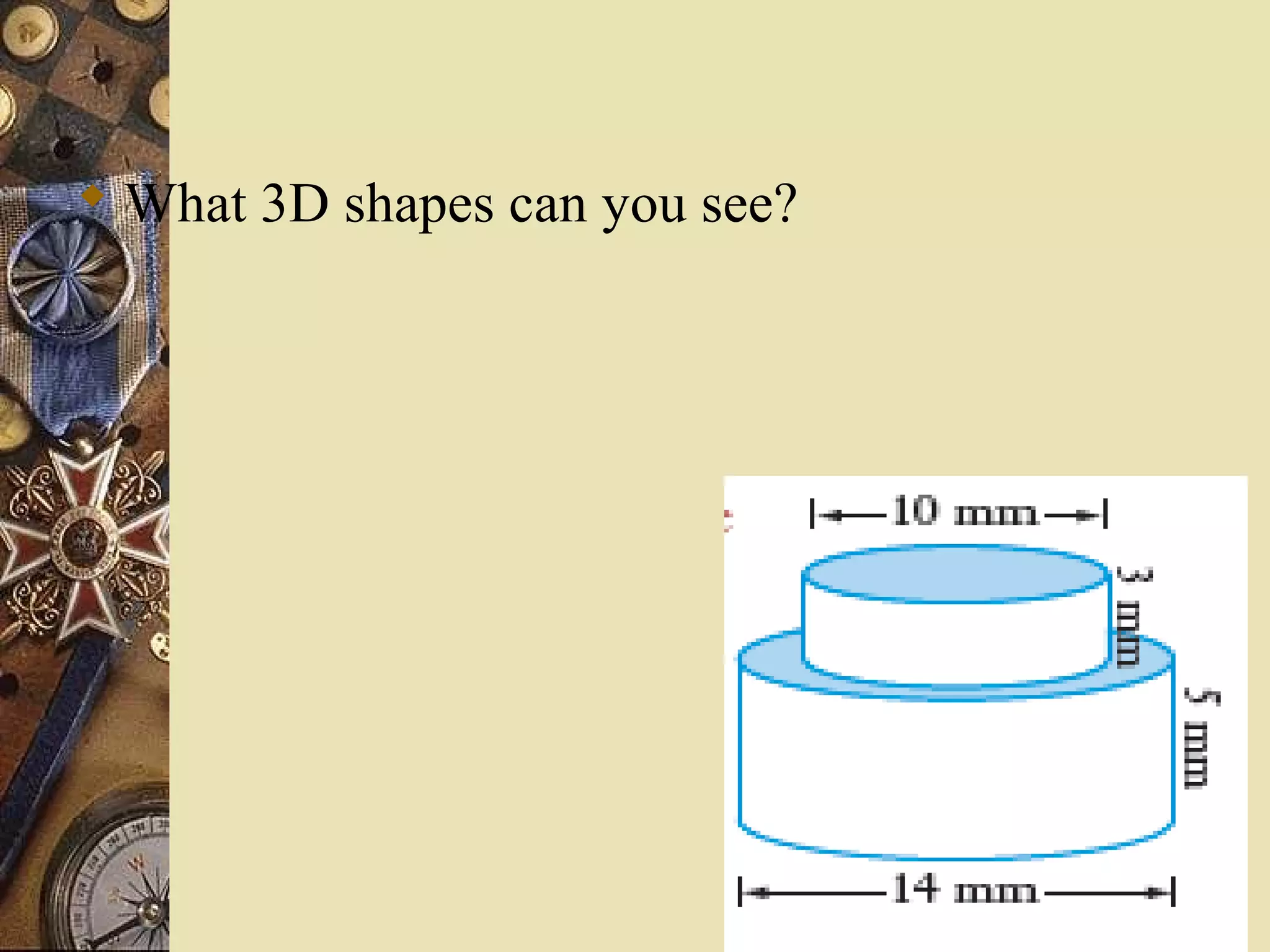
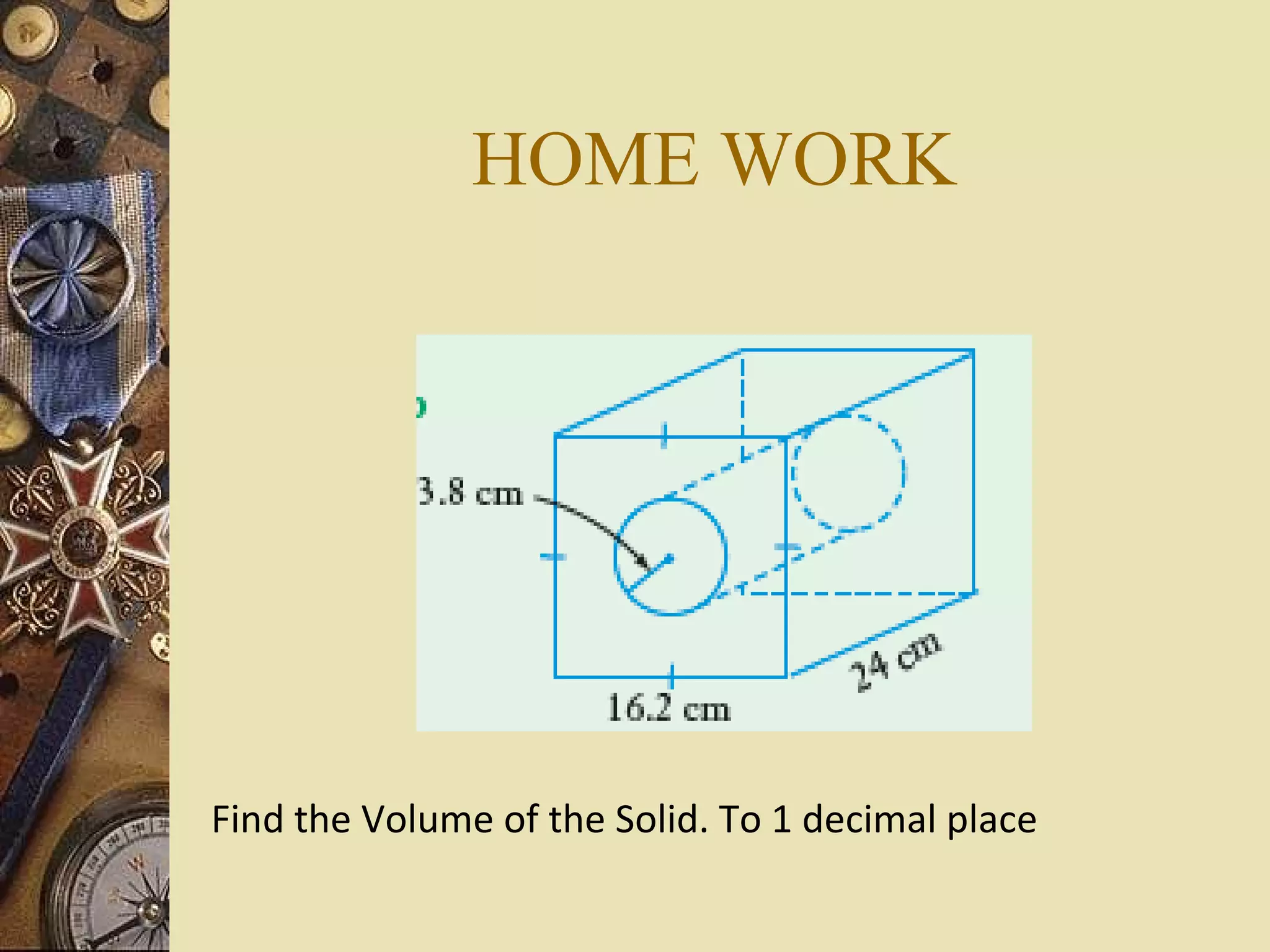
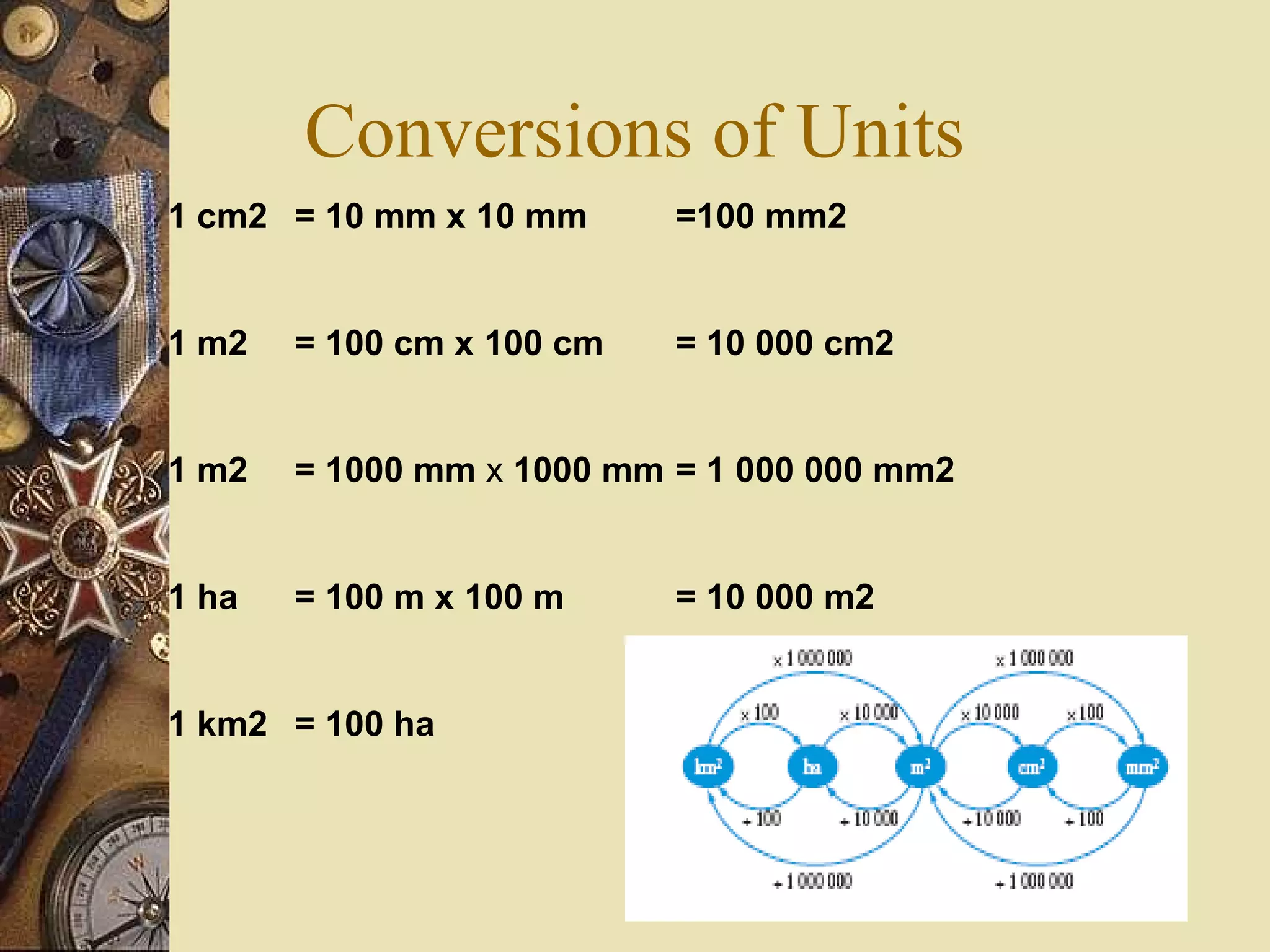
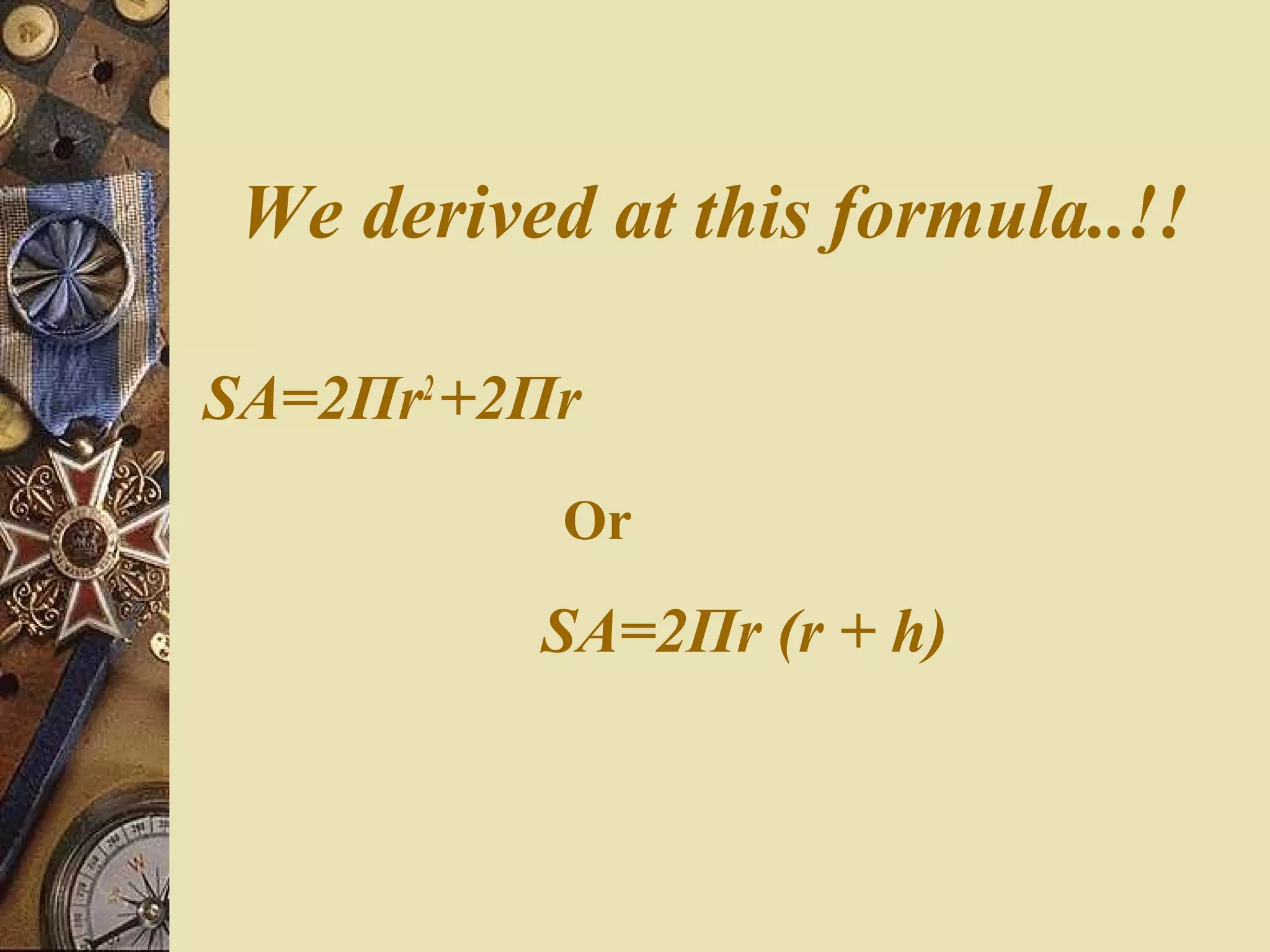The document provides a comprehensive lesson on calculating the surface area and volume of various geometric shapes, including cylinders, cuboids, and cones. Key formulas, examples, and step-by-step calculations are given to enhance students' understanding of surface area and volume measurement. The lesson includes practical applications and a series of exercises for students to practice these concepts.

1. K.V
Faridkot
Harkamalpreet
Singh Brar
9 -B
th

2. Topic

3. Objectives
 At the end of the lesson the students
should be able;
To find the surface area of a
cylinder ..

4. What is a cylinder?
 The term Cylinder refers to a right
circular cylinder. Like a right prism, its
altitude is perpendicular to the bases
and has an endpoint in each base.

5. PRESENTATION
base
altitude
radius
base

6. What will happen if we
removed the end of the
cylinder and unrolled the
body?
Lets find out
!!!!

7. This will happen if we unrolled
and removed the end of a
cylinder….
h
Circumference
of the base
2Πr 2

8. Notice that we had formed 2
circles and a 1 rectangle….
 The 2 circles serves as our bases of
our cylinder and the rectangular
region represent the body

9. How can we solved the surface
area of a Cylinder?
 To solve the surface area of a
cylinder, add the areas of the
circular bases and the area of
the rectangular region which is
the body of the cylinder.

10. This is the formula in order to
solved the surface are of a
cylinder.
 SA= area of 2 circular bases
+ are of a rectangle
oR

11. We derived at this formula..!!
SA=2Πr2 +2Πr
Or
SA=2Πr (r + h)

12. Find the surface area of a
cylindrical water tank given the
height of 20m and the radius of
5m? (Use π as 3.14)
Given:
SA=2πr2 +2πrh
h=20m
r=5m =2(3.14)(5m)2 + 2[(3.14)
(5m)(20m)
=157m2 + 628m
SA =785m2

13. 2-Surface Area of a Prism
Cubes and Cuboids

14. Surface area of a cuboid
To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The top and the bottom of the
cuboid have the same area.

15. Surface area of a cuboid
To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The front and the back of the
cuboid have the same area.

16. Surface area of a cuboid
To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The left hand side and the right
hand side of the cuboid have
the same area.

17. Surface area of a cuboid
To find the surface area of a shape, we calculate the
total area of all of the faces.
Can you work out the
5 cm
8 cm surface area of this cubiod?
The area of the top = 8 × 5
= 40 cm2
7 cm The area of the front = 7 × 5
= 35 cm2
The area of the side = 7 × 8
= 56 cm2

18. Surface area of a cuboid
To find the surface area of a shape, we calculate the
total area of all of the faces.
5 cm So the total surface area =
8 cm
2 × 40 cm2 Top and bottom
7 cm + 2 × 35 cm2 Front and back
+ 2 × 56 cm2 Left and right side
= 80 + 70 + 112 = 262 cm2

19. Formula for the surface area of a cuboid
We can find the formula for the surface area of a cuboid
as follows.
Surface area of a cuboid =
w
l
2 × lw Top and bottom
h + 2 × hw Front and back
+ 2 × lh Left and right side
= 2lw + 2hw + 2lh

20. Surface area of a cube
How can we find the surface area of a cube of length x?
All six faces of a cube have the
same area.
The area of each face is x × x = x2
Therefore,
x
Surface area of a cube = 6x2

21. Checkered cuboid problem
This cuboid is made from alternate purple and green
centimetre cubes.
What is its surface area?
Surface area
=2×3×4+2×3×5+2×4×5
= 24 + 30 + 40
= 94 cm2
How much of the
surface area is green?
48 cm2

22. Surface area of a prism
What is the surface area of this L-shaped prism?
3 cm
To find the surface area of
3 cm
this shape we need to add
together the area of the two
4 cm L-shapes and the area of the
6 rectangles that make up
6 cm the surface of the shape.
Total surface area
= 2 × 22 + 18 + 9 + 12 + 6
+ 6 + 15
5 cm = 110 cm2

23. Using nets to find surface area
It can be helpful to use the net of a 3-D shape to calculate its
surface area.
Here is the net of a 3 cm by 5 cm by 6 cm cubiod.
6 cm
Write down the
area of each
3 cm 18 cm2 3 cm
6 cm face.
Then add the
5 cm 15 cm2 30 cm2 15 cm2 30 cm2
areas together
to find the
surface area.
3 cm 18 cm2 3 cm
Surface Area = 126 cm2

24. Using nets to find surface area
Here is the net of a regular tetrahedron.
What is its surface area?
Area of each face = ½bh
= ½ × 6 × 5.2
= 15.6 cm2
5.2 cm Surface area = 4 × 15.6
= 62.4 cm2
6 cm

25. 3-Warm up: Finding the Area of a
Lateral Face
 Architecture. The lateral faces of the
Pyramid Arena in Memphis, Tennessee,
are covered with steal panels. Use the
diagram of the arena to find the area of
each lateral face of this regular pyramid.

26. Pyramid Arena
mynameismr.info/.../Surface%20Area%20of%20Pyramids%20&%20Cones.ppt

27. mynameismr.info/.../Surface%20Area%20of%20Pyramids%20&%20Cones.ppt

28. Surface Area of a Cone
Unit 6, Day 4
Ms. Reed
With slides from www.cohs.com/.../229_9.3%20Surface%20Area%20of
%20Pyramids%20and%20Cones%20C...

29.  A cone has a circular base and a vertex that is not in the same plane as
a base.
 In a right cone, the height meets the base at its center.
The vertex is directly
Height above the center of
the circle.
Lateral Surface
Slant Height
r
Base
r
 The height of a cone is the perpendicular distance between the vertex
and the base.
 The slant height of a cone is the distance between the vertex and a
point on the base edge.

30. Surface Area of a Cone
 Surface Area = area of base + area of sector
= area of base + π(radius of base)(slant height)
S = B + π r l = π r + π rl 2
l
B =πr 2 r

31. Lateral Area of a Cone
 Since Lateral Area = Surface Area – area of the
base
= π r + π rl
L.A. = 2

32. Example 1:
 Find the surface area of the cone to the nearest
whole number.
a. 4 in. r = 4 slant height = 6
S = π r + π rl
2
= π (4) + π (4)(6)
2
6 in.
= 16π + 24π
= 40π
= 40(3.14)
≈ 126in. 2

33. Example 2:
 Find the surface area of the cone to the nearest whole
number.
b. l
5 ft.
12 ft.
First, find the slant height. Next, r = 12, l = 13.
l =r +h
2 2 2 S = π r + π rl
2
= (12) + (5)
2 2 = π (12) + π (12)(13)
2
= 144 + 25 = 169 = 144π + 156π
= 300π
l = 169 = 13 ≈ 942 ft. 2

34. On your own #1
Calculate the surface
area of:
S = π r 2 + π rl
•S = π(7)2 + π(7)(11.40)
•S = 49π + 79.80π
•S = 128.8π

35. On your own #2
Calculate the lateral area of:
S = π r = π rl
L.A. +
2
•L.A. = π(5)(13)
•L.A. = 65π

36. Homework
Work Packet:
Surface Area of Cones

37. 4-Surface Area of a
Sphere

38. Sphere

39. Hemisphere

40. Great Circle

43. (Surface Area of a Sphere) = 4πr2

44. 5-Basic Geometric
Properties
Volume of a
cuboid

45. In this lesson you will learn
to calculate the volume of a
cuboid

46. Cuboids

47. Look at this cuboid
Now imagine it is full
of cubic centimetres
6 cm
1 cm3
4 cm
10 cm
Can you see that there are 10 × 4 = 40 cubic centimetres on the
bottom layer?
There are 6 layers of 40 cubes making 40 × 6 = 240 cm3

48. Let us go back and look at what we did here
6 cm
height
4 cm
breadth
10 cm
length
When we worked out the volume we multiplied the length by the
breadth and then by the height
Volume of a cuboid = length × breadth × height
or
V=lbh

49. Lets us look again
at the same
cuboid and this 6 cm
time try the
formula
4 cm
10 cm
V=lbh
= 10 × 4 × 6 cm3
= 240 cm3
You will see that this is the same answer as we got before

50. 6-Volume of a Cylinder

51. What is Volume?
 The volume of a three-dimensional figure
is the amount of space within it.
 Measured in Units Cubed (e.g. cm3)

52. Volume of a Prism
 Volume of a Prism is calculated by
Volume = Area of cross section x perpendicular height
V = Ah
V = (4 x 4) x 4 = 64 m3

53. What is this?
 It has 2 equal shapes at the base, but it is
not a prism as it has rounded sides
It is a Cylinder

54. Volume of a Cylinder
 How might we find the Volume of a
Cylinder?

55. Example
 V = Ah

56. Pieces Missing
 Find the volume of concrete used to make this
pipe
 Volume of Concrete = Volume of Big
Cylinder – Volume of Small Cylinder (hole)

57.  What shape is present here?

58.  What 3D shapes can you see?

59. HOME WORK
Find the Volume of the Solid. To 1 decimal place

60. Homework/Challenge
 Challenge Question

61. Volume of a Cylinder
 How might we find the Volume of a
Cylinder?
 V = Ah
–=

62. Conversion of units
 1cm – 10mm
 1m – 100cm
 1km – 1000m

63. Conversions of Units
1 cm2 = 10 mm x 10 mm =100 mm2
1 m2 = 100 cm x 100 cm = 10 000 cm2
1 m2 = 1000 mm x 1000 mm = 1 000 000 mm2
1 ha = 100 m x 100 m = 10 000 m2
1 km2 = 100 ha

64. What about when cubic units?
 1 cm3
 = 1cm x 1cm x 1cm
 = 10 mm × 10 mm × 10 mm
 = 1000 mm3
 1 m3
 = 1m x 1m x 1m
 = 100 cm × 100 cm × 100 cm
 = 1 000 000 cm3

65. Capacity
 Volume - The volume of a three-dimensional
figure is the amount of space within it.
 Measured in Units Cubed (e.g. cm3)
 Volume and capacity are related.
 Capacity is the amount of material (usually
liquid) that a container can hold.
 Capacity is measured in millilitres, litres and
kilolitres.

66. Examples of Capacity

67. How does Volume relate to
Capacity?
 1000 mL = 1 L
 1000 L = 1 kL
 1 cm3 = 1 mL
 1,000cm3 = 1000ml = 1L
 1 m3 = 1000 L = 1 kL

68. Examples
 Convert 1800 mL to L
 1800ml = 1800/1000
= 1.8L
 2.3 m3 to L 1m3 = 1000L
(1kL)
 2.3m3 = 2.3kL
= 2300L

69. Length = 5.53cm
Capacity
 Find the Capacity of this cube
 Length = 5.53cm
 V = Ah
 = (5.53 x 5.53) x 5.53
 = 169.11cm3 (1cm3 =
1ml)
 Capacity = 169.11ml

70. Example
 Find the capacity of this rectangular prism.
 Solution
 Volume = Ah
 = (26 x 12) x5
 = 312 × 5
 = 1560 cm3 (1cm3 = 1mL)
 Capacity = 1560 mL or 1.56 L (1000mL
= 1L)

71. Ex 11.08 – Q 7.

72.  What size rainwater tank would be needed to
hold the run-off when 40 mm of rain falls on a
roof 12 m long and 3.6 m wide? (Answer in
litres.)

73. 7-Volume of Cones

74. Volume of Cylinders
 Volume = Base x height
 V = Bh
B
 Base area = π r2 r
h

75. Compare Cone and Cylinder
 Use plastic space figures.
 Fill cone with water.
 Pour water into cylinder.
 Repeat until cylinder is full.
r r
h

76. Volume of Cone?
=
 3 cones fill the cylinder, so…
 Volume = ⅓ Base x height

77. Volume of Cone
 3 cones fill the cylinder
 Volume = ⅓ Base x height
 V = ⅓ Bh h = 7 cm
 Base area = π r2
 V = ⅓ (π . 2.5 2) . 7 r =2.5 cm
 V = ⅓ 3.14 . 6.25 . 7

78. 8-Developing the Formula for the
Volume of a Sphere

79. Volume of a Sphere
Using relational solids and pouring material we noted
that the volume of a cone is the same as the volume of a
hemisphere (with corresponding dimensions)
Using “math language” Volume (cone) = ½ Volume (sphere)
Therefore 2(Volume (cone)) = Volume (sphere)
OR =
+

80. Volume of a Sphere
We already know the formula for the volume of a cone.
Volumecylinder
Volumecone =
3
OR = ÷3

81. Volume of a Sphere
AND we know the formula for the volume of a cylinder
Volumecylinder = ( Area of Base ) X (Height )
Height
BASE

82. Volume of a Sphere
SUMMARIZING:
Volume (cylinder) = (Area Base) (height)
Volume (cone) = Volume (cylinder) /3
= ÷3
Volume (cone) = (Area Base) (height)/3
AND 2(Volume (cone)) = Volume (sphere)
2X =

83. Volume of a Sphere
2(Volume (cone)) = Volume (sphere)
2X =
2(Area of Base) (height) /3= Volume (sphere)
2( πr2)(h)/3= Volume (sphere)
r
BUT h = 2r h
r
2(πr )(2r)/3 = Volume(sphere)
2
4(πr3)/3 = Volume(sphere)

84. 3
4π r 
Volume of a Sphere 4 π r 3
3 3
3
4π r 
Volumesphere =
3
4 π r 3 4 π r 3
3 3