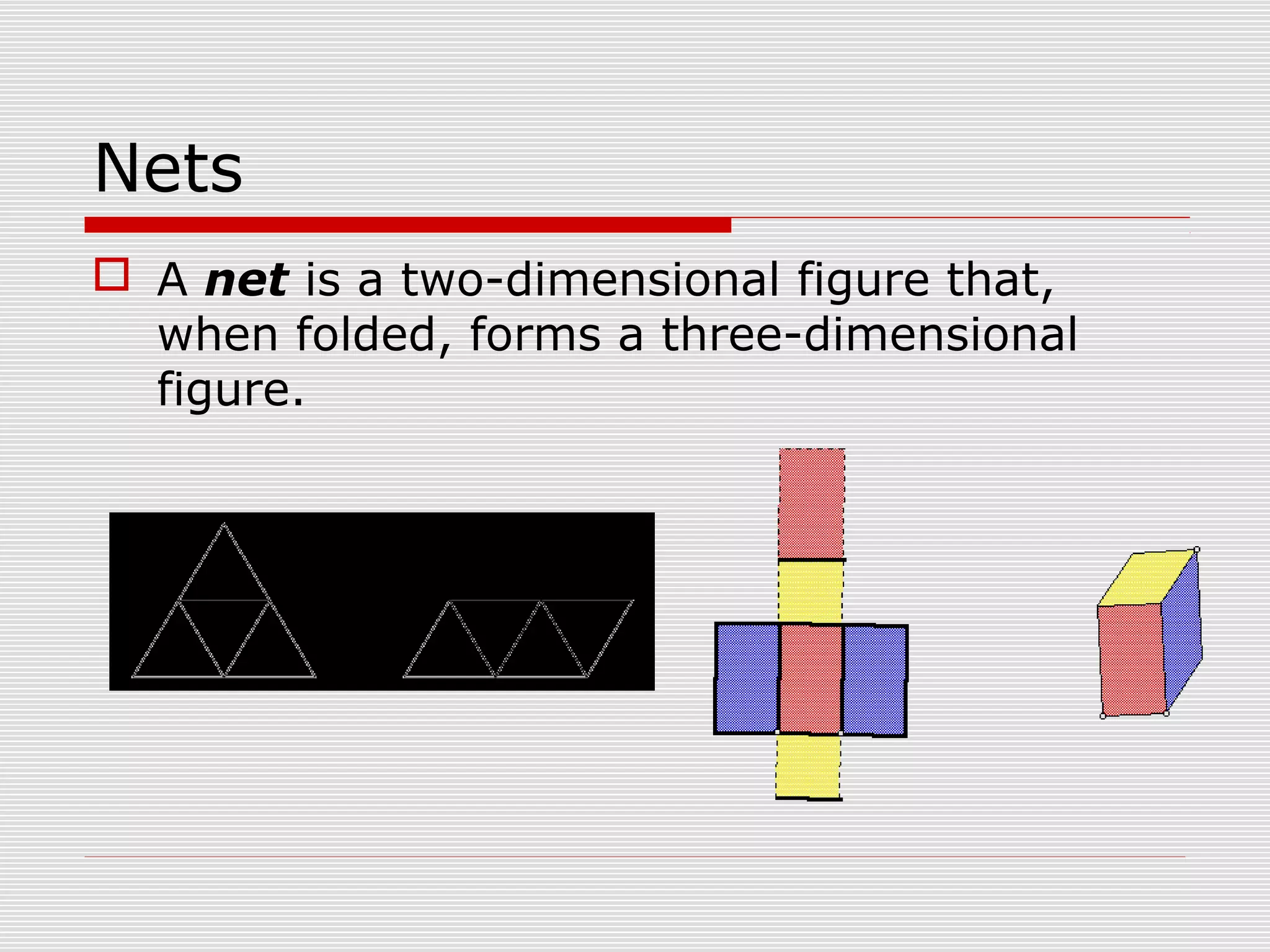
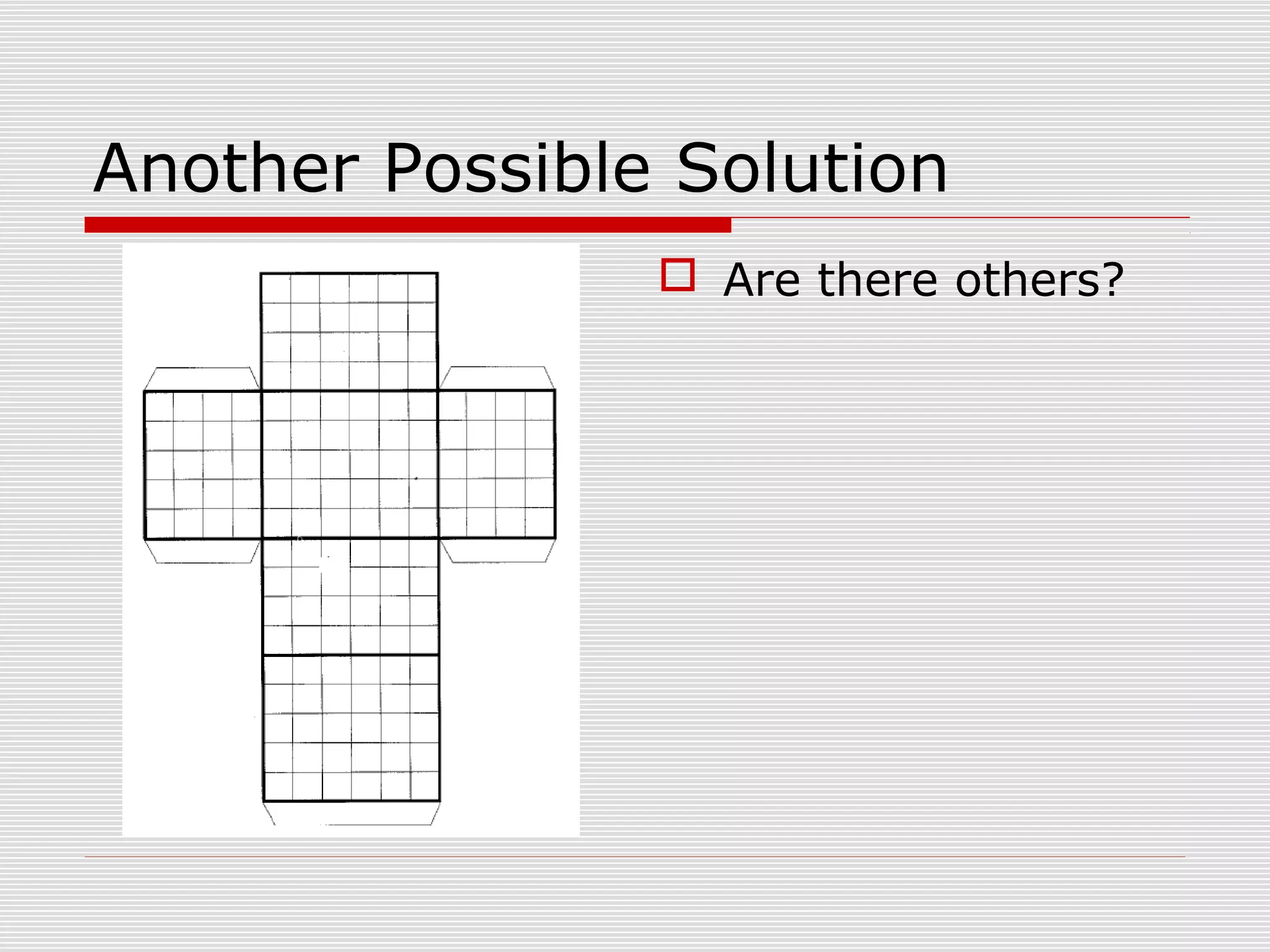
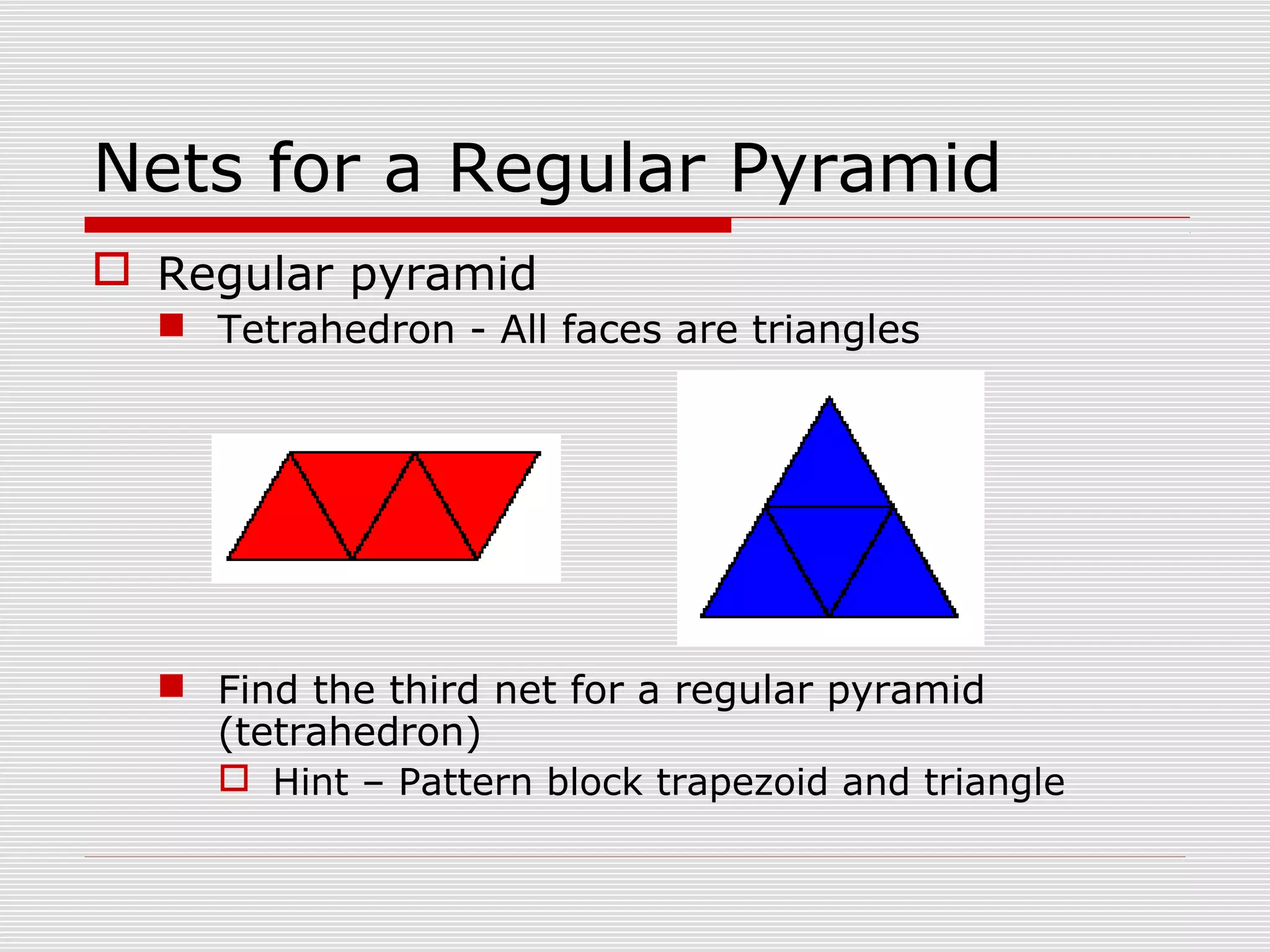
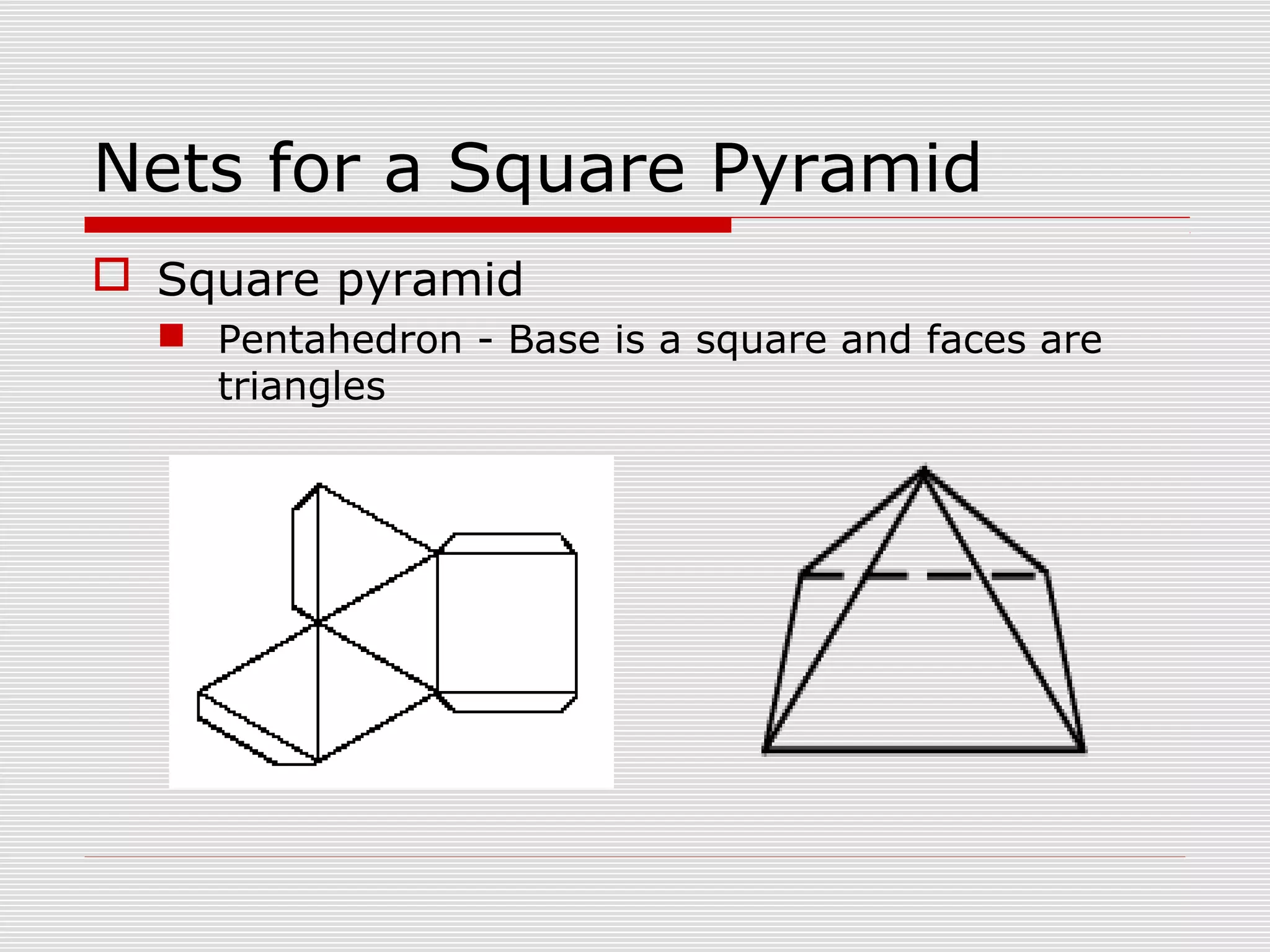
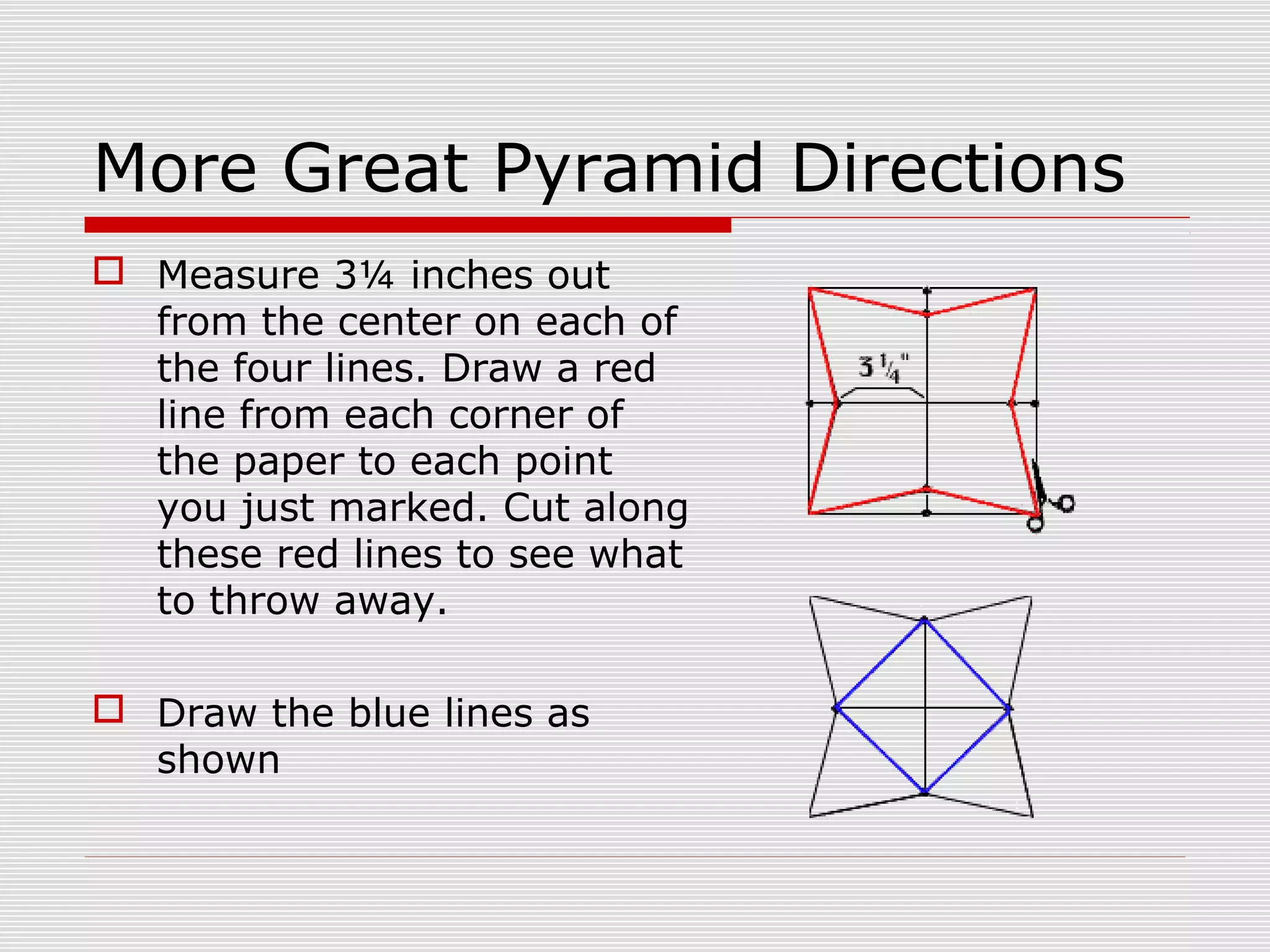
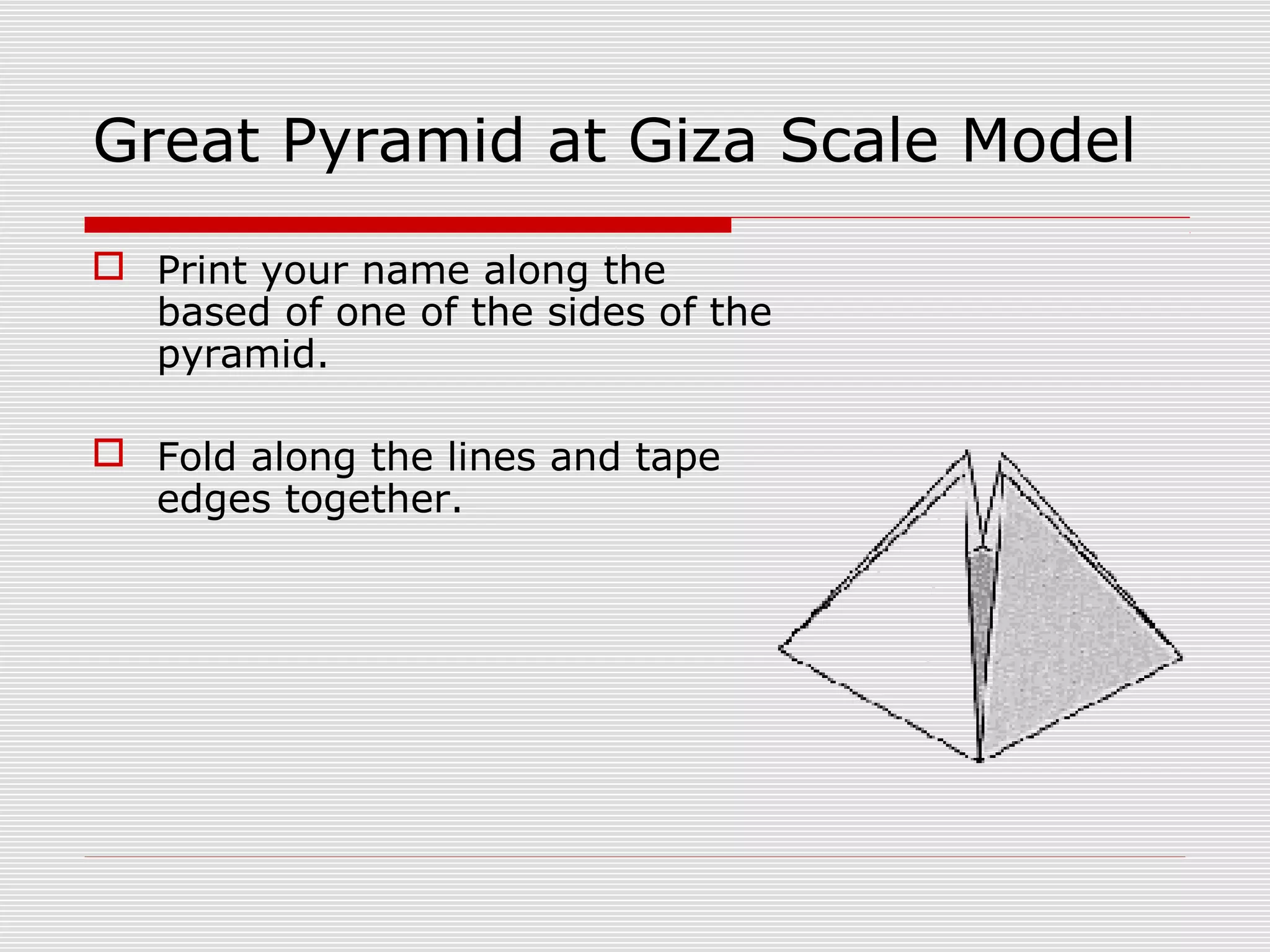
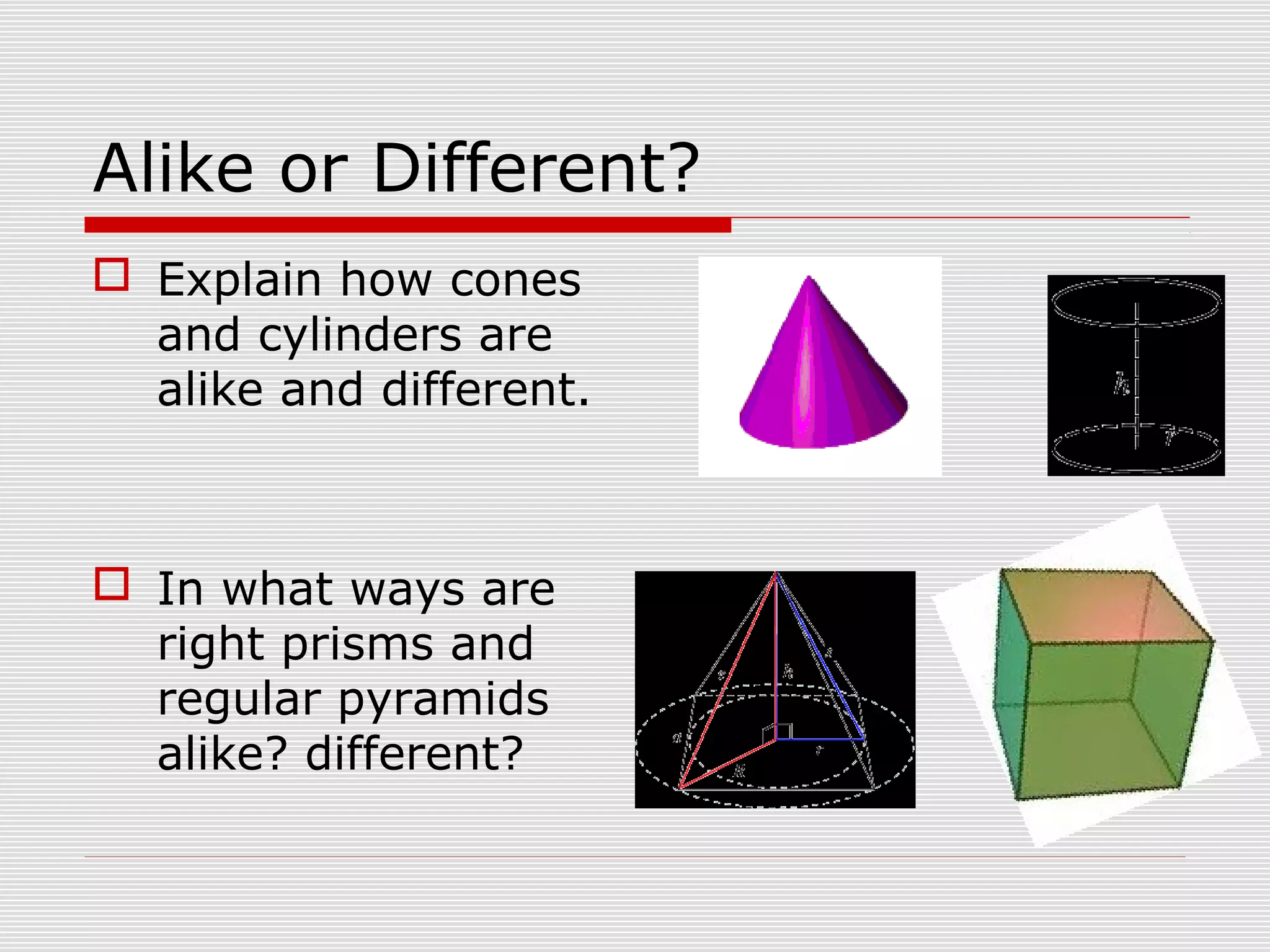
This document provides information about nets and how to construct them for various three-dimensional geometric shapes such as cubes, rectangular prisms, pyramids, cylinders, and cones. It includes directions for folding nets to create models and investigations into properties of shapes made from different nets. The document contains overviews of key aspects of nets, examples of specific nets, and questions or activities for students to explore nets and the relationships between two-dimensional net patterns and the three-dimensional shapes they form.

1. Nets
 A net is a two-dimensional figure that,
when folded, forms a three-dimensional
figure.

2. Identical Nets
 Two nets are identical if they are
congruent; that is, they are the same if
you can rotate or flip one of them and it
looks just like the other.

3. Nets for a Cube
 A net for a cube can be drawn by tracing
faces of a cube as it is rolled forward,
backward, and sideways.
 Using centimeter grid paper
(downloadable), draw all possible nets for
a cube.

4. Nets for a Cube
 There are a total of 11 distinct (different)
nets for a cube.

5. Nets for a Cube
 Cut out a copy of the net below from centimeter grid
paper (downloadable).
 Write the letters M,A,T,H,I, and E on the net so that
when you fold it, you can read the words MATH
around its side in one direction and TIME around its
side in the other direction.
 You will be able to orient all of the letters except one
to be right-side up.

6. Nets for a Rectangular Prism
 One net for the yellow rectangular
prism is illustrated below. Roll a
rectangular prism on a piece of paper
or on centimeter grid paper and trace
to create another net.

7. Another Possible Solution
 Are there others?

8. Nets for a Regular Pyramid
 Regular pyramid
 Tetrahedron - All faces are triangles
 Find the third net for a regular pyramid
(tetrahedron)
 Hint – Pattern block trapezoid and triangle

9. Nets for a Square Pyramid
 Square pyramid
 Pentahedron - Base is a square and faces are
triangles

10. Nets for a Square Pyramid
 Which of the following are nets of a square
pyramid?
 Are these nets distinct?
 Are there other distinct nets? (No)

11. Great Pyramid at Giza
 Construct a scale model from net to geometric
solid (downloadable*)
 Materials per student:
 8.5” by 11” sheet of paper
 Scissors
 Ruler (inches)
 Black, red, and blue markers
 Tape
*http://www.mathforum.com/alejandre/mathfair/pyram
id2.html (Spanish version available)

12. Great Pyramid at Giza Directions
 Fold one corner of the paper
to the opposite side. Cut off
the extra rectangle. The
result is an 8½" square sheet
of paper.
 Fold the paper in half and in
half again. Open the paper
and mark the midpoint of
each side. Draw a line
connecting opposite
midpoints.
4 ¼”
8 ½”

13. More Great Pyramid Directions
 Measure 3¼ inches out
from the center on each of
the four lines. Draw a red
line from each corner of
the paper to each point
you just marked. Cut along
these red lines to see what
to throw away.
 Draw the blue lines as
shown

14. Great Pyramid at Giza Scale Model
 Print your name along the
based of one of the sides of the
pyramid.
 Fold along the lines and tape
edges together.

15. Nets for a Cylinder
 Closed cylinder (top and bottom included)
 Rectangle and two congruent circles
 What relationship must exist between the
rectangle and the circles?
 Are other nets possible?
 Open cylinder - Any rectangular piece of
paper

16. Surface Area of a Cylinder
 Closed cylinder
 Surface Area = 2*Base area + Rectangle area
 2*Area of base (circle) = 2*πr2
 Area of rectangle = Circle circumference * height
= 2πrh
 Surface Area of Closed Cylinder =
(2πr2
+ 2πrh) sq units
 Open cylinder
 Surface Area = Area of rectangle
 Surface Area of Open Cylinder = 2πrh sq units

17. Building a Cylinder
 Construct a net for
a cylinder and form
a geometric solid
 Materials per
student:
 3 pieces of 8½”
by 11” paper
 Scissors
 Tape
 Compass
 Ruler (inches)

18. Building a Cylinder Directions
 Roll one piece of paper to form an
open cylinder.
 Questions for students:
 What size circles are needed for
the top and bottom?
 How long should the diameter or
radius of each circle be?
 Using your compass and ruler,
draw two circles to fit the top and
bottom of the open cylinder. Cut
out both circles.
 Tape the circles to the opened
cylinder.

19. Can Label Investigation
 An intern at a manufacturing plant is given
the job of estimating how much could be
saved by only covering part of a can with a
label. The can is 5.5 inches tall with diameter
of 3 inches. The management suggests that 1
inch at the top and bottom be left uncovered.
If the label costs 4 cents/in2
, how much would
be saved?

20. Nets for a Cone
 Closed cone (top or bottom
included)
 Circle and a sector of a larger
but related circle
 Circumference of the (smaller)
circle must equal the length of
the arc of the given sector
(from the larger circle).
 Open cone (party hat or ice
cream sugar cone)
 Circular sector

21. Cone Investigation
 Cut 3 identical sectors from 3 congruent circles or use
3 identical party hats with 2 of them slit open.
 Cut a slice from the center of one of the opened cones
to its base.
 Cut a different size slice from another cone.
 Roll the 3 different sectors into a cone and secure with
tape.
Questions for Students:
 If you take a larger sector of the same circle, how is
the cone changed? What if you take a smaller sector?
 What can be said about the radii of each of the 3
circles?

22. Cone Investigation continued
 A larger sector would increase the area of the base
and decrease the height of the cone.
 A smaller sector would decrease the area of the
base and increase the height.
 All the radii of the same circle are the same length.

23. Making Your Own Cone Investigation
 When making a cone from an 8.5” by
11” piece of paper, what is the
maximum height? Explain your
thinking and illustrate with a drawing.

24. Creating Nets from Shapes
 In small groups students create nets for
triangular (regular) pyramids
(downloadable isometric dot paper), square
pyramids, rectangular prisms, cylinders,
cones, and triangular prisms.
 Materials needed – Geometric solids, paper
(plain or centimeter grid), tape or glue
Questions for students:
 How many vertices does your net need?
 How many edges does your net need?
 How many faces does your net need?
 Is more than one net possible?

25. Alike or Different?
 Explain how cones
and cylinders are
alike and different.
 In what ways are
right prisms and
regular pyramids
alike? different?

26. Nets for Similar Cubes Using
Centimeter Cubes
 Individually or in pairs,
students build three similar
cubes and create nets
 Materials:
 Centimeter cubes
 Centimeter grid paper
Questions for Students
 What is the surface area of
each cube?
 How does the scale factor
affect the surface area?