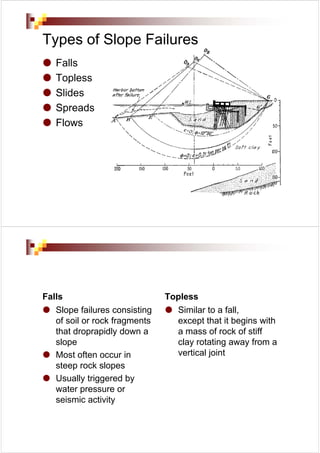
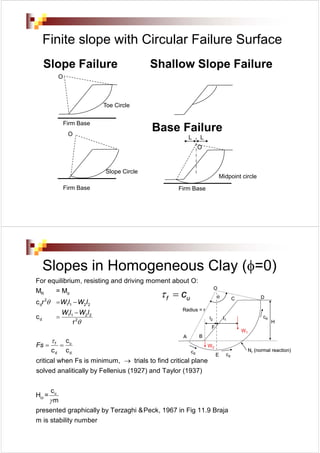
Slope failures can occur in different modes such as falls, topples, slides, spreads, and flows. Slides are further classified into rotational, translational, and complex composite types. Slope stability analysis involves calculating the factor of safety (Fs) which is the ratio of shear strength to shear stress developed along the potential failure surface. An Fs greater than 1.5 indicates stable conditions. Methods for analyzing slope stability include infinite slope analysis, finite slope analysis using plane or circular failure surfaces, and modern methods using soil properties and the method of slices. Computer programs are commonly used to perform detailed slope stability evaluations.

1. Slope Stability
updated June 7, 2007
Haryo Dwito Armono, M.Eng, Ph.D

2. Types of Slope Failures
Falls
Topless
Slides
Spreads
Flows
Falls Topless
Slope failures consisting
p g Similar to a fall,
of soil or rock fragments except that it begins with
that droprapidly down a a mass of rock of stiff
slope
l clay rotating away from a
l t ti f
Most often occur in vertical joint
steep rock slopes
Usually triggered by
water pressure or
seismic activity

3. Slides Spreads
Slope failures that
p Similar to translational
involve one ore more slides except that the
blocks of earth that block separate and
move ddownslope b
l by move apart as they also
t th l
shearing along well move outward
defined surfaces or thin Can be very destructive
shear zones
Flows Types of Slides
Downslope movement of
p Rotational slides
earth where earth Most often occur in
resembles a viscous homogeneous materials
fluid
fl id such as fills or soft clays
Mudflow can start with a Translational slides
snow avalanche, or be in
avalanche Move along planar shear
surfaces
conjuction with flooding
Compound slides
Complex and composite
slides

4. The driving force (g
g (gravity) overcomes the
y)
resistance derived from the shear strength of
the soil along the rupture surface
g p
Slope stability analysis
Calculation to check the safety of natural
slopes, slopes of excavations and of
compacted embankments.
t d b k t
The check involves determining and
comparing the shear stress de eloped
developed
along the most likely rupture surface to
the shear strength of soil.

5. Factor of Safety
τf
Fs =
τd
Fs = factor of safety with respect to strength
τ f = average shear strength of the soil
τ d = average s ea st ess de e oped a o g t e potential failure su ace
a e age shear stress developed along the pote t a a u e surface
τ f = c + σ tan φ
c = cohesion
φ = angle of friction
σ = average normal stress on the potential failure surface
similarly
τ d = cd + σ tan φd
subscript 'd' refer to p
p potential failure surface
c + σ tan φ
Fs =
cd + σ tan φd
when Fs = 1, the slope is in a state of impending of failure.
In general Fs > 1.5 is acceptable
Stability of Slope
Infinite slope without seepage
Infinite slope with seepage
Finite slope with Plane Failure Surface
(Cullman s
(Cullman's Method)
Finite slope with Circular Failure Surface
(Method of Slices)

6. Infinite slope
L
c tan φ
β Fs = +
γ H cos2 β tan β tan β
d
a F
W
Na
B For granular soils, c=0 Fs is independent
soils c 0,
F Ta
c of height H, and the slope is stable as
H
long as β < φ
b Tr
β N
A r
R
L
d
Direction of
γ ' tan φ
a seepage
W c
Na
F =
Fs +
γ sat H cos2 β tan β γ sat tan β
B
Ta
c
H
T
β b r β N
A r
R
Finite slope with Plane Failure Surface
B C
W β + φd
Na
θcr =
Ta 2
τ f = c + σ tan φ
H unit weight of soil = γ
4c ⎡ sin β cos φ ⎤
Tr Nr
R
Hcr =
A
β θ γ ⎢ 1 − cos( β − φ ) ⎥
⎣ ( ⎦

7. Finite slope with Circular Failure Surface
Slope Failure Shallow Slope Failure
O
Toe Circle
Firm Base
O
Base Failure
L L
O
Slope Circle
Midpoint circle
Firm Base Firm Base
Slopes in Homogeneous Clay (φ=0)
For equilibrium, resisting and driving moment about O:
τ f = cu
O
MR = Md
θ C D
c dr 2θ = W1l1 − W2 l 2
Radius = r
W l −W l
cd = 11 2 2 2 l2 l1 cd
rθ H
F
W1
A B
τf cu
Fs = = W2
cd cd cd Nr (normal reaction)
E cd
critical when Fs is minimum, → trials to find critical plane
solved analitically by Fellenius (1927) and Taylor (1937)
cu
Hcr =
γm
presented graphically by Terzaghi &Peck, 1967 in Fig 11.9 Braja
m is stability number

8. Swedish Slip Circle Method
Slopes in Homogeneous Clay (φ>0)
τ f = c + σ tan φ
c d = γ H ⎡f (α , β ,θ ,φ ) ⎤
⎣ ⎦
c
= f (α , β ,θ ,φ ) = m
γ Hcr
where m is stability number

9. Method of Slices
For equilibrium
Nr = Wn cos α n
n=p
∑ ( c ΔL n + Wn cos α n tan φ )
Fs = n =1
n=p
∑W
n =1
n sin α n
bn
ΔLn ≈ where b is the width of nth slice
cos α n
Bishop Method
Bishop (1955) refine solution to the previous
method of slices.
In his method, the effect of forces on the sides
of each slice are accounted for some degree .
n=p
1
∑ ( cb
n =1
n + Wn tan φ )
mα ( n )
Fs = n=p
∑Wn =1
n sin α n
where
tan φ sin α n
mα ( n ) = cos α n +
Fs
The ordinary method of slices is presented as
learning tools. It is rarely used because is too
tools
conservative

10. Computer Programs
STABL
GEO-SLOPE
etc
Bibliography
Holtz, R.D and Kovacs, W.D., “An Introduction to Geotechnical
An
Engineering”
Das, B.M., “Soil Mechanics”
Das, B.M., “Advanced Soil Mechanics”