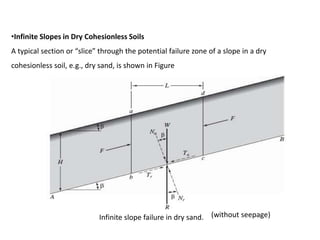
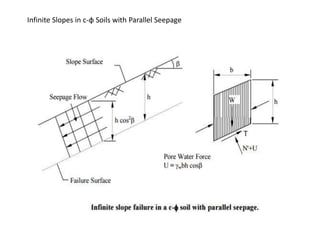
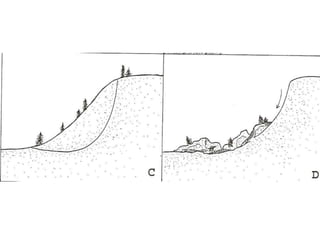
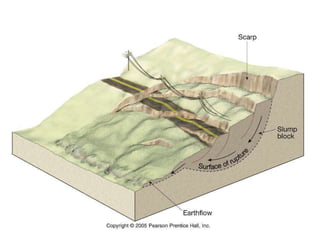
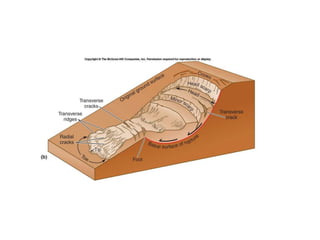
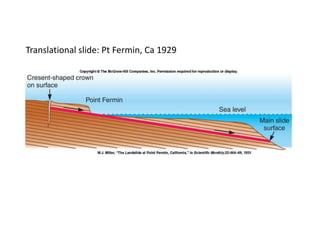
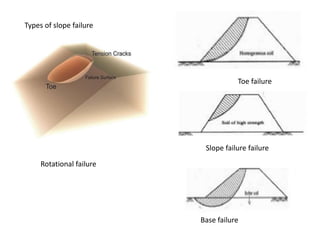
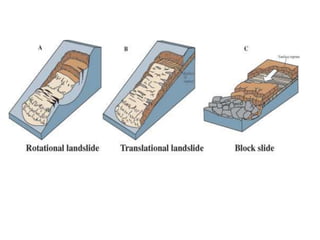
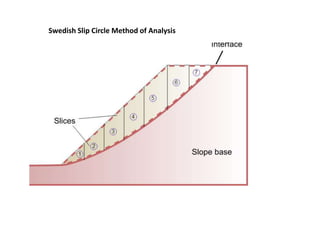
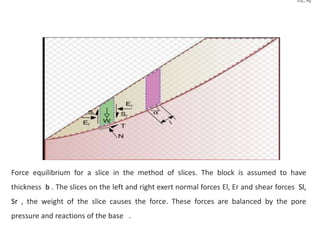
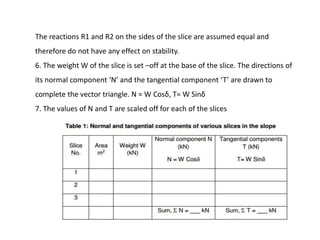
1) Slope stability is analyzed using the factor of safety, which is the ratio of resisting shear strength to driving shear stress. A factor of safety below 1.5 indicates instability. 2) Common slope failure modes include rotational, toe, base, and transitional failures. The Swedish circle method divides a potential failure surface into slices to analyze stability. 3) Factors that influence slope stability include soil properties, geometry, drainage conditions, and external loads. Various techniques can improve stability, such as flattening slopes, installing drainage, or adding retaining structures.

1. Stability of slopes

11. Translational slide: Pt Fermin, Ca 1929

12. Translational slide: Pt Fermin, Ca 1929

14. An exposed ground surface that stands at an angle with the horizontal is called an
unrestrained slope. slope. The slope can be natural or constructed. If the ground surface
is not horizontal, a component of gravity will cause the soil to move downward
If the component of gravity is large enough, slope failure can occur; that is, the soil
mass in zone abcdea can slide downward. The driving force overcomes the resistance
from the shear strength of the soil along the rupture surface.

15. Types of slope failure
Rotational failure
Toe failure
Slope failure failure
Base failure

17. This type of failure occurs by rotation along a slip surface by downward and
outward movement of the soil mass. The slip surface is generally circular and soil
is generally homogeneous.
1) Toe failure:- the slope failure occurs when the failure surface intersect
the slope at toe.
2) Base failure:- the base failure occur when the failure surface passes
through the base of the slope
3) Slope failure:- when failure surface passes through the slope surface.

18. Transitional failure:-
In practice the slope having in
homogenious soil for a considerable
length fail under transitional failure

19. The task of the engineer charged with analyzing slope stability is to determine the factor
of safety. Generally, the factor of safety is defined as
where
FSs: factor of safety with respect to strength
τf average shear strength of the soil
τ d average shear stress developed along the potential failure surface
The shear strength of a soil consists of two components, cohesion and friction,
and may be expressed as

20. Where ϕd and cd are the shear parameters along the developed potential failure
surface. By all above equations,
Fc and Fϕ together results in to the Fs
Now we can introduce some other aspects of the factor of safety—that is, the factor of
safety with respect to cohesion, FSc, and the factor of safety with respect to
friction, FS. They are defined as follows:

21. we see that when FSc becomes equal to FS, that is the factor of safety with respect to
strength. Or, if
When FSs is equal to 1, the slope is in a state of impending failure. Generally, a value
of 1.5 for the factor of safety with respect to strength is acceptable for the design of
a stable slope.

22. •Infinite Slopes in Dry Cohesionless Soils
A typical section or “slice” through the potential failure zone of a slope in a dry
cohesionless soil, e.g., dry sand, is shown in Figure
Infinite slope failure in dry sand. (without seepage)

23. equal and opposite and may be ignored. The effective weight of the soil element
is (with pore water pressure equal to 0)
Eq:-1

24. (2) (2)
(3)

25. For an infinite slope analysis, the FS is independent of the slope depth, h, and depends
only on the angle of internal friction, φ, and the angle of the slope, β. The slope is said
to have reached limit equilibrium when FS=1.0. Also, at a FS = 1.0, the maximum slope
angle will be limited to the angle of internal friction, φ.

26. Infinite Slopes in c-φ Soils with Parallel Seepage

28. By substituting W = γsat b h into the above expression and rearranging terms, the FS is
given by:
From Equation ,it is apparent that for a cohesionless material with parallel
seepage, the FS is also independent of the slope depth, h, just as it is for a dry
cohesionless material

29. The difference is that the FS for the dry material is reduced by the factor γ'/γsat for
saturated cohesionless materials to account for the effect of seepage. For typical soils,
this reduction will be about 50 percent in comparison to dry slopes.

30. Swedish Slip Circle Method of Analysis

31. Force equilibrium for a slice in the method of slices. The block is assumed to have
thickness b . The slices on the left and right exert normal forces El, Er and shear forces Sl,
Sr , the weight of the slice causes the force. These forces are balanced by the pore
pressure and reactions of the base .

32. •In the method of slices,, the sliding mass above the failure surface is divided into a
number of slices. The forces acting on each slice are obtained by considering the
mechanical (force and moment) equilibrium for the slices.
•Each slice is considered on its own and interactions between slices are neglected
because the resultant forces are parallel to the base of each slice.
•However, Newton's third law is not satisfied by this method because, in general, the
resultants on the left and right of a slice do not have the same magnitude and are not
collinear

33. For a c-φ soils the undrained strength envelope shows both c and φ values. The total
stress analysis can be adopted. The procedure is follows
1. Draw the slope to scale
2. 2. A trail slip circle such as AB with radius ‘r’ is drawn from the center of rotation
O.
3. Divide the soil mass above the slip surface into convenient number of slices (more
than 5 is preferred)
4. Determine the area of each slice A1, A2, -------, An A = width of the slice X mid
height = b X Z
5. Determine the total weight W including external load if any as W = γ b Z = γ A
Where, γ = unit weight b = width of slice Z = height of slice.

34. The reactions R1 and R2 on the sides of the slice are assumed equal and
therefore do not have any effect on stability.
6. The weight W of the slice is set –off at the base of the slice. The directions of
its normal component ‘N’ and the tangential component ‘T’ are drawn to
complete the vector triangle. N = W Cosδ, T= W Sinδ
7. The values of N and T are scaled off for each of the slices

35. For the ordinary method of slices, the resultant vertical and horizontal forces are
The calculations are generally done in tabular form it is repeated for number of trial
surfaces and the surface which gives minimum F.S. is considered the most critical
surface.
Repeat step 2 to 9 by considering various trial slip circles and calculate FS for each of
these slip circles. The slip circle with a minimum FS is called critical slip circle.

36. •Improvement of stability of slopes:-
•The slopes that are prone to failure and collapse by sliding can be enhanced and made
serviceable, safe and secure. For this numerous efficient and reliant methods are used
to stabilize the slopes. The methods usually engage one or more of the following
measures, which either reduce the mass that are vulnerable to cause the sliding and
collapse or successfully helps improving the shear strength of the soil in the failure
zone.
1) Slope flattening reduces the weight of the mass tending to slide/collapse. It can be
employed wherever possible.
2) Proving a berm beneath the toe of the slope enhances the resistance to movement.
It is especially useful when there is a possibility of a base line.

37. 4) Densification by the using explosives, vibroflotation or terra probe aids in increasing
the shear strength of cohesionless soils and hence increases stability.
5) Consolidation by surcharging, electro-osmosis or various other reliable effective
methods help in enhancing the stability of slopes in cohesive soils.
6) Grouting and injection of cement concrete mixture along with other compounds into
specific zones help in increasing the stability of slopes.
3) Drainage helps in reducing the seepage forces and thus enhances the stability of
slopes. The zone of subsurface water is lowered and infiltration of the surface water
is prevented.

38. 7)Sheet piles and retaining wall structures can be installed to provide lateral support
and to increase the stability.
8)Stabilization of the soil helps in enhancing the stability of slopes.
9) Other relative inexpensive methods like for slope flattening and drainage control
may be usually applied

39. In a slope the component of the self weight (γ) causes instability and the cohesion
contributes to stability. The maximum height (Hc) of a slope is directly proportional
to unit cohesion (Cu) and inversely proportional to unit weight (γ) . In addition, Hc is
also related to friction angle (φu) and slope angle β.
Stability Number

40. Stability of upstream slope during sudden drawdown : For the upstream
slope of an earth dam the most critical condition occurs when the reservoir is
suddenly emptied without allowing appreciable drainage from the saturated soil
mass. This condition is known as sudden drawdown.
When sudden drawdown take place, the weight of water which is still present in the
soil tends to cause sliding of the wedge, as the water pressure which was acting on
the u/s slope to balance this weight has been suddenly removed.
According to another interpretation, the shearing resistance of the soil is
considerably reduced due to pore pressure existing in the soil, whereas the
disturbing force due to saturated unit weight of the soil remains the same.

41. To take into account this fact in stability analysis the pore water pressures determined
along the portion of the slip surface which lies below the water surface obtaining the
net effective resisting forces and the actuating (disturbing) forces are calculated by
taking the saturated weight of soil mass which lies below water surface, this case also
the pore water pressure may be determine by drawing the flownet .