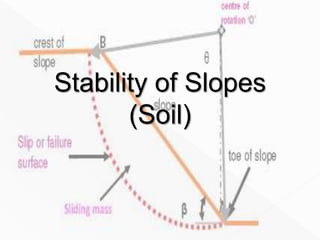
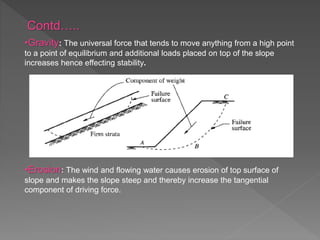
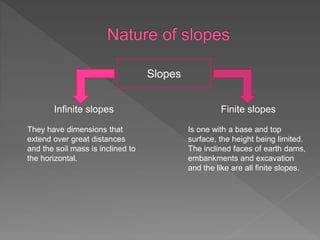
This document discusses slope stability and different types of slope failures including translational and rotational. It describes factors that affect slope stability such as erosion, water seepage, earthquakes, and gravity. Methods for analyzing slope stability are presented, including infinite slope analysis, Culmann's method, friction circle method, method of slices, Bishop's method, and Spencer's method. The key parameters in analyzing slope stability are the factor of safety and stability number.

1. Stability of Slopes
(Soil)

2. Slope & Slope stability of
Soil

3. Failures
Translational type
• Failure of slope along weak zone
of soil.
• Sliding mass travel long distance
before coming to rest.
• Common in coarse grained soil.
Rotational type
• Common in fine grained soils.
• An imaginary axis –point
theory exist along which slope
is said to rotate to reach a
stable position.
• Can be circular & non-circular

4. Erosion
Water Seepage force
Sudden Drawdown
Earthquakes
Gravity

5. •Gravity: The universal force that tends to move anything from a high point
to a point of equilibrium and additional loads placed on top of the slope
increases hence effecting stability.
•Erosion: The wind and flowing water causes erosion of top surface of
slope and makes the slope steep and thereby increase the tangential
component of driving force.
Contd…..

6. •Water Seepage force: Seepage
forces in the sloping direction add to
gravity forces and make the slope
susceptible to instability. The pore water
pressure decrease the shear strength.
This condition is critical for the
downstream slope
•Sudden Drawdown:
In this case there is reversal in the
direction flow and results in instability of
side slope. Due to sudden drawdown the
shear stresses are more due to saturated
unit weight while the shearing resistance
decreases due to pore water pressure
that does not dissipate quickly.

7. •Earthquakes: They induce dynamic
shear forces. In addition there is
sudden buildup of pore water pressure
that reduces available shear strength.

8. Slopes
Natural
•Hilly & Valley slopes.
•River terraces and coastal
cliffs.
Man-made
•Embankment for highways and earth
dams.
•Excavation dumps and waste heaps for
landfill.
•Landscape development

10. Slopes
Infinite slopes
They have dimensions that
extend over great distances
and the soil mass is inclined to
the horizontal.
Finite slopes
Is one with a base and top
surface, the height being limited.
The inclined faces of earth dams,
embankments and excavation
and the like are all finite slopes.

11. Def: Factor of safety of a slope is defined as the ratio of average shear
strength ( 𝜏f ) of a soil to the average shear stress ( 𝜏d) developed along
the potential failure surface.

12. The shearing strength mobilized at each point on a failure surface (10.2)
FoS for cohesion and internal friction if different the eq. of mobilsed
shearing resistance (10.3)

15. Infinite slope (SAND)
Assumptions,
β=angle of infinite slope w.r.t horizontal, a cohesion-less soil slope.

16. If the slope is stable,
slope angle limits to angle
of cohesion
FoS of an infinite slope of
sand

17. Infinite slope (CLAY)
CONDITION 1:No seepage, no pore pressure.
Vertical stress:
Components of
stress:
Value substitution: Allowable height

18.  Stability number=
•A dimensionless quantity, is directly proportional to
required cohesion an is inversely proportional to
allowable height.
Factor of safety,
Critical height

19. CONDITION 2: (A) Seepage parallel to ground
surface
Normal stress:
Shear stress:
Hence, if FoS=1,
Then stability number=

20. CONDITION 2: (B) Slope completely submerged
under water and no seepage
Stability number=
Where,

22. Finite slope
Steps for investigation:
•Assumptions of possible failure surface
•Equilibrium forces acting on the slope.
Methods of Analysis:
 Culmann method (Planar failure).
 Method considering whole free body:
- Slope failure under undrained condition.
- Friction-circle method.
- Tailor stability number
 Method of slice (Swedish c-φ method)

23. Culmann’s Method: for planar
failure surface
Assumptions,
• failure of a slope occurs along a plane
when the average shearing stress
tending to cause the slip is more than
the shear strength of the soil.
• Also, the most critical plane is the one
that has a minimum ratio of the
average shearing stress that tends to
cause failure to the shear strength of
soil.
Methods of Analysis

24. Culmann’s Method……
Solving the equations, and substituting
&

25. Types of Rotational (Circular)
failure
Face (Slope) failure
Toe failure
Base failure

26. Face (Slope) failure
• This type of failure occurs
when the slope angle (β) is
large and when the soil at
the toe portion is strong.

27. Toe failure
• In this case the failure surface
passes through the toe. This
occurs when the slope is steep
and homogeneous.
toe

28. Base failure
• In this case the failure
surface passes below the toe.
This generally occurs when
the soil below the toe is
relatively weak and soft.
Base failed

29. Failure under undrained conditions (φu=0):
Assumptions,
• Soil is homogeneous.
• Potential failure surface is a circular arc.
• This is seen in fully saturated, undrained soil.
 Two failure types
Slope failure
Base failure

30. Factor of safety
Contd….

31. Friction-circle method

32. Contd….
Factor of safety using frictional-circle method

33. Tailor’s stability number:
• Taylor (1937) conceived the idea of analyzing the stability of a
large number of slopes through a wide range of slope angles and
angles of internal friction, and then representing the results by an
abstract number which he called the "stability number".
Stability number
&
Factor of safety

34. Tailor’s chart:
Fos plot Fφ’ vs Fc’ to find Fs

35. • In this procedure, the soil above the surface of sliding is divided
into a number of vertical parallel slices. The stability of each slice
is calculated separately. This is a versatile technique in which the
non homogeneity of the soils and pore water pressure can be
taken into consideration. It also accounts for the variation of the
normal stress along the potential failure surface.
Method of slices:

36. Method of slices: for steady seepage
Graphical method:

37. Contd….

38. Method of slices: Bishop’s method
•A simplified and more refined solution.
• Useful if slope contains different kind of soil
with different C-φ.
Here,
W = weight of the slice
N = total normal force on the failure surface
cd
U = pore water pressure = ul on the failure
surface cd
FR = shear resistance acting on the base of
the slice
Er E2 - normal forces on the vertical faces be
and ad
Tr T2 = shear forces on the vertical faces be
and ad
θ = the inclination of the failure surface cd to
the horizontal

39. =FoS by conventional method
Where, frictional
resistance
And,
Solving and substituting,
Factor of safety
Contd….

40. Bishop’s and Morgenstern method:

41. Spencer method:
•Bishop’s method satisfies the
equation of equilibrium w.r.t
moment but not with force.
Factor of safety:

42. The charts developed by Spencer for
different values of Ns, φ'm and ru:
a
b
c
Worked out example: