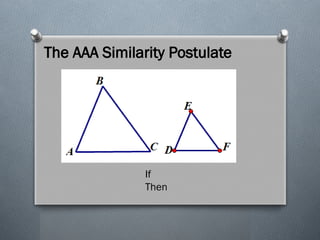
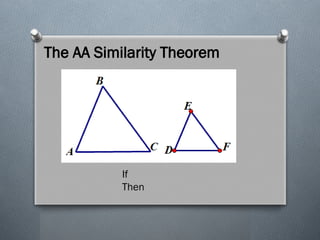
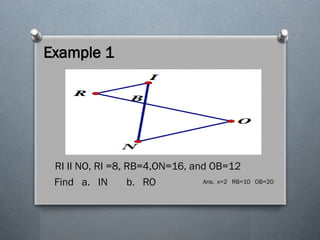
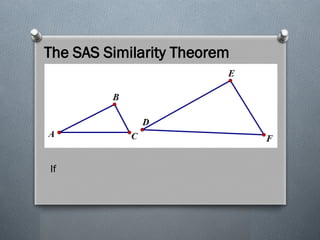
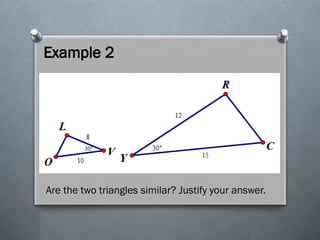
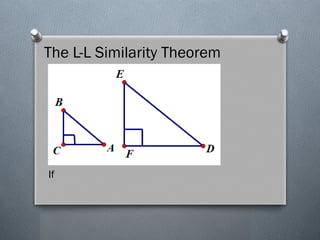
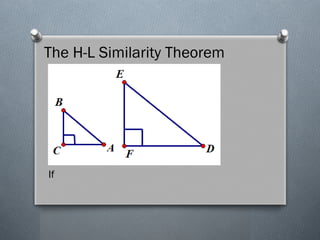
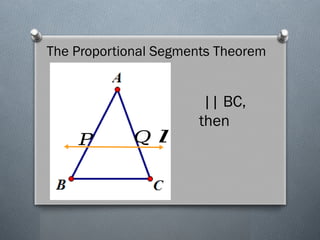
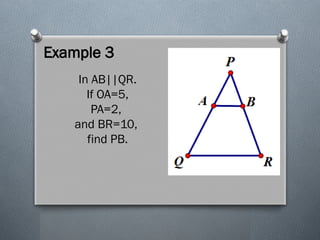
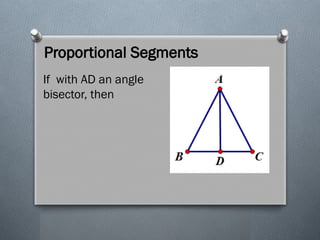
The document discusses the various theorems regarding the similarity of triangles, including the AAA, AA, SAS, SSS, L-L, and H-L similarity theorems, which provide conditions under which triangles are considered similar based on their angles and side ratios. It also covers the proportional segments theorem, which states that a line parallel to one side of a triangle divides the other two sides proportionally. Additionally, it explains how an angle bisector divides the opposite side into segments proportional to the adjacent sides.

1. Similar Triangles

2. The AAA Similarity Postulate
If three angles of one triangle are
congruent to three angle of
another triangle, then the two
triangles are similar.

3. The AAA Similarity Postulate
If
Then

4. The AA Similarity Theorem
If
Then

5. Example 1
RI II NO, RI =8, RB=4,ON=16, and OB=12
Find a. IN b. RO Ans. x=2 RB=10 OB=20

6. The SAS Similarity Theorem
If two sides of one triangle are
proportional to the corresponding
two sides of another triangle and
their respective included angles
are congruent, then the triangles
are similar.

7. The SAS Similarity Theorem
If

8. Example 2
Are the two triangles similar? Justify your answer.

9. The SSS Similarity Theorem
If the sides of one triangle are
proportional to the corresponding
sides of a second triangle, then
the triangles are similar.

10. Similar right triangles
The L-L Similarity Theorem
If the legs of a right triangle are
proportional to the corresponding
legs of another right triangle, the
right triangles are similar.

11. The L-L Similarity Theorem
If

12. Similar right triangles
The H-L Similarity Theorem
If the hypotenuse and a leg of a
right triangle are proportional to
the corresponding hypotenuse and
leg of another right triangle, then
the right triangles are similar.

13. The H-L Similarity Theorem
If

14. Proportional Segments
The Proportional Segments Theorem
If a line intersects two sides of a
triangle at distinct points and is
parallel to the third side, the line
divides the two sides in two
proportional segments.

15. The Proportional Segments Theorem
𝑙
𝑄
𝑃
|| BC,
then

16. Example 3
In AB||QR.
If OA=5,
PA=2,
and BR=10,
find PB.

17. Proportional Segments
The Bisector of an angle of a triangle
divides the opposite side into
segments which are proportional to the
adjacent sides.

18. Proportional Segments
If with AD an angle
bisector, then