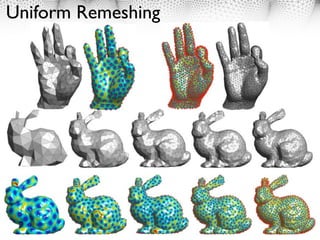
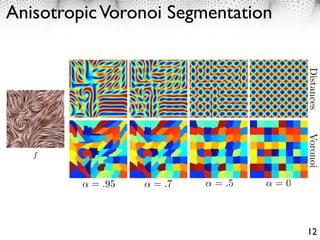
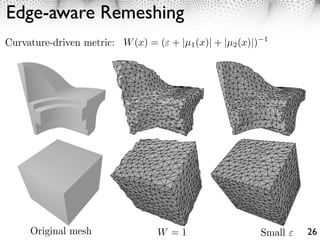
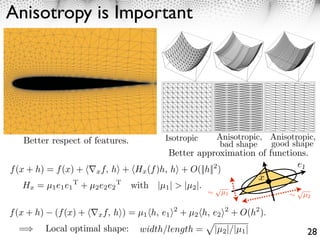
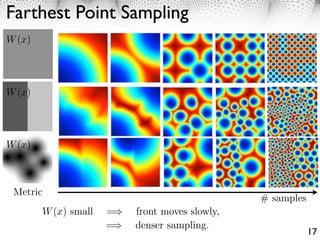
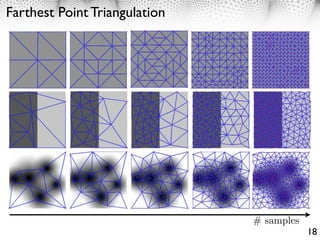
1. Geodesic sampling and meshing techniques can be used to generate adaptive triangulations and meshes on Riemannian manifolds based on a metric tensor. 2. Anisotropic metrics can be defined to generate meshes adapted to features like edges in images or curvature on surfaces. Triangles will be elongated along strong features to better approximate functions. 3. Farthest point sampling can be used to generate well-spaced point distributions over manifolds according to a metric, which can then be triangulated using geodesic Delaunay refinement.

1. Geodesic Sampling and Meshing
http://www.ceremade.dauphine.fr/~peyre/
Gabriel Peyré
CEREMADE, Université Paris Dauphine

2. Overview
•Riemannian Metrics.
• Riemannian Voronoi and Delaunay.
• Farthest Point Sampling.
• Anisotropic Triangulations.
• Anisotropic Delaunay Refinement.
2

3. Riemannian Manifold
Riemaniann manifold: abstract parametric space M Rn .
Metric: M equiped x ⇥ M ⇤ H(x) ⇥ Rn n positive definite.
1⇥
def. T
Length of a curve (t) M: L( ) = (t) H( (t)) (t)dt.
Examples: 0
Euclidean space: M = Rn and H(x) = Idn .
2D shape: M R2 and H(x) = Id2 .
Parametric surface: H(x) = Ix first fundamental form.
Isotropic metric: H(x) = W (x)Idn , W (x) > 0 weight function.
Image processing: I : [0, 1]2 ⇥ R, W (x) = ( + ||⇤x I||) 1
.
DTI imaging: M = [0, 1]3 , H(x) =di usion tensor.
W (x)
3

4. Geodesic Distances
Geodesic distance metric over M Rn
def.
⇥ (x, y) M2 , dM (x, y) = min L( )
T >0, PT (x,y)
def.
where PT (x, y) = { (0) = x and (T ) = y} .
Geodesic curve: (t) such that L( ) = dM (x, y).
def.
Distance map to a starting1057 x0
2 ECCV-08 submission ID
point M: Ux0 (x) = dM (x0 , x).
metric
geodesics
Euclidean Shape Isotropic Anisotropic Surface 4

5. Overview
• Riemannian Metrics.
• Riemannian Voronoi and Delaunay.
• Farthest Point Sampling.
• Anisotropic Triangulations.
• Anisotropic Delaunay Refinement.
5

6. Euclidean Delaunay Triangulation
Delaunay graph DS : (xi , xj ) ⇤ DS ⇥ Ci ⌃ Cj ⌅= ⇧.
6

7. Euclidean Voronoi Segmentation
7

8. Euclidean Delaunay Triangulation
Delaunay graph DS : (xi , xj ) ⇤ DS ⇥ Ci ⌃ Cj ⌅= ⇧.
8

9. Geodesic Voronoi and Delaunay
Voronoi segmentation:
Outer cell: C0 = Closure( c
).
Delaunay graph DS : (xi , xj ) ⇤ DS ⇥ Ci ⌃ Cj ⌅= ⇧.
9

10. Voronoi Diagrams on Surfaces
10

11. Double and Triple Points
S large enough = DS is a planar triangulation.
Double point: wi,j = argmin d(x, xi ).
x Ci ⇥Cj
Tripple point: si,j,k Ci ⇥ Cj ⇥ Ck .
si,j,k xk
xi xj
Fast computation in O(n log(n))
with Fast Marching. wi,j
Geometric realization of DS :
Union of two geodesics starting from wi,j .
Special case: boundary curves if xi and xj . 11

12. Anisotropic Voronoi Segmentation
ECCV-08 submission ID1057 7
Distances
Voronoi
f
= .95
= .1 = .2
= .7 = .5
= .5 =1
= 0
Fig. 4. Examples of anisotropic distances (top row) and Voronoi diagrams (bottom
row) with an decreasing anisotropy . The metric tensor is computed using the structure
tensor, equation (8).
12

13. Overview
• Riemannian Metrics.
• Riemannian Voronoi and Delaunay.
•Farthest Point Sampling.
• Anisotropic Triangulations.
• Anisotropic Delaunay Refinement.
13

14. Coverings and Packings
14

15. Geodesic Delaunay and Voronoi
xi,j,k xi
xk xi,j
x
xj xi,j,
15

16. Farthest Point Sampling
Surface sampling {x1 , . . . , xn } M.
⇤ ⇤
Parametric domain sampling: : [0, 1] ⇥
2
M, xi,j = (i/ n, j/ n).
def.
-covering: i B (xi ) = M, where B (x) = {y dM (x, y) }.
-separated: min(dM (xi , xj )) .
1. Initialization: x1 random, d(x) dM (x0 , x), set i = 1.
Farthest point
2. Select point: xi+1 = argmaxx d(x), = d(xi+1 ).
3. Local update of the distance: d(x) min(d(x), dM (xi+1 , x)).
4. Stop: If i < n or > 0 , set i i + 1 and go back to 2.
Theorem: The sampling {x1 , . . . , xn } is an -covering that is -separated for
= max min dM (xi , xj ).
i=1,...,n j=1,...,n
16

17. Farthest Point Sampling
W (x)
W (x)
W (x)
Metric
# samples
W (x) small = front moves slowly,
= denser sampling.
17

18. Farthest Point Triangulation
# samples
18

19. Meshing a Planar Shape
Uniform
Adaptive
19

20. Uniform Remeshing
20

21. Remeshing of the David
Original: Remeshed:
100k vert. 10k vert.
21

22. Adaptive Remeshing
# samples
22

23. Density Given by a Texture
Parameterized surface: :D [0, 1]2 ⇥ S R3 .
Texture: I = [0, 1]2 R.
⇥p S, W (p) = ( + ||⇤ 1 (p) I||) 1
I( 1
(p))
|| 1 (p) I|| W =1 large small 23

24. Curvature of a Height field
Height field: x ⇥ [0, 1]2 (x, f (x)) ⇥ R3 .
f (x + h) = f (x) + ⇤x f, h⇥ + Hx (f )h, h⇥ + O(||h||2 )
Hx = µ1 e1 e1 T + µ2 e2 e2 T with |µ1 | > |µ2 |.
f (x + h) (f (x) + ⇥⌅x f, h⇤) = µ1 ⇥h, e1 ⇤2 + µ2 ⇥h, e2 ⇤2 + O(h2 ).
x e1 (x)
e2 (x)
Gaussian curvature: µ1 (x)µ2 (x) = det(Hx (f )).
Intrinsic
Mean curvature: (µ1 (x) + µ2 (x))/2 = tr(Hx (f ))/2.
Total curvature: |µ1 (x)| + |µ2 (x)|. Extrinsic
24

25. Curvature of a Surface
Parametric surface: x ⇥ R2 ⇤ (x) ⇥ R3 .
⇥ ⇥ ⇥ ⇥
Normal: n = ⇥x1 ⇥x2 / ⇥x1 ⇥x2 .
⇥ 2 (x) ⇥
Second fundamental form: Hx = , n(x)⇥
⇥xi ⇥xj i,j=1,2
Numerical estimation:
• polynomial fit.
• local covariance analysis.
|µ1 (x)| + |µ2 (x)|. 25

26. Edge-aware Remeshing
Curvature-driven metric: W (x) = ( + |µ1 (x)| + |µ2 (x)|) 1
Original mesh W =1 Small 26

27. Overview
• Riemannian Metrics.
• Riemannian Voronoi and Delaunay.
• Farthest Point Sampling.
•Anisotropic Triangulations.
• Anisotropic Delaunay Refinement.
27

28. Anisotropy is Important 8 Jonathan Richard Shewchuk
Better respect of features. Isotropic Anisotropic, Anisotropic,
Figure 2: A visual illustration of how large angles, but not small angles, can cause the error f− g to
bad shape good shape
explode. In each triangulation, 200 triangles are used to render a paraboloid.
Better approximation of 20
40
20 functions.
40
40 e1
f (x + h) = f (x) + ⇤x f, h⇥ + Hx (f )h, h⇥ + O(||h|| ) 2
35 65
50 20
40
x
Hx = µ1 e1 e1 + µ2 e2 e2
T T
with |µ1 | > |µ2 |.
Figure 3: As the large angle of the triangle approaches 180◦ , or the sliver tetrahedron becomes arbitrarily
⇥
flat, the magnitude of the vertical component of g becomes arbitrarily large.
⇥
µ1 µ2
sphere, then perturbing one of the vertices just off the equator so that the sliver has some (but not much)
volume.
f (x + h) (f (x) + ⇥⌅x f, h⇤) = µ1 ⇥h, ge1and2not+−µ2,⇥h, cangenerators+ O(h2 ). elements. Section 6.1 presents
, ⇤ which ebe ⇤
Because of this sensitivity, mesh
f g ∞
2 usually choose the shapes of elements to control f −
2 reduced simply by using smaller
∞
quality measures that judge the shape of elements based on their fitness for interpolation.
= Local optimal shape: width/length = “weaker butf2−|/|µ1 |a triangle.3c r firstisupperasbound is almost tight,
to within a factor of two. The |µ simpler upper bound” of The not good an indicator as
Table 2 gives two upper bounds on g over ∞
t circ
28
the stronger upper bound, but it has the advantages of being smooth almost everywhere (and therefore more

29. TheFor a geometricallyinterpolation ff2 that is C (V, T ) is C edges, one cani )however ibuilt an⇥ is
piecewise linear regular image ⇥ , of f on outside such that fM (x = f (x ) and fM
2 2
⇥
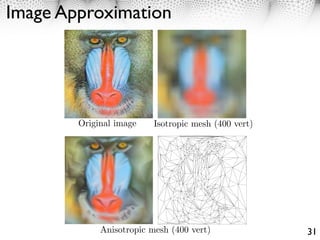
Approximation of Images with Edges
||f fM⇥
j
2
CM .
M
basis. The following theorem sketch the construction of such a triangulation.
(9.2)
linear on each triangular face t|| . This is a two-dimensional extension performance of a wavelet
adapted triangulation that enhances significantly the approximation of the spline approximations
. We give here only a sketch ofThis9.4. Geometric Image Approximationdepends on the position of the vertices
studied in Section ??. the proof. [todo linear approximationtubes] Near an edges,
piecewise : show an image of the
ngths of thethe connectivity T of the M 1 and their widths should be of order M 2 . We
V and triangles should be of order triangulation. In order to e⇥ciently approximate a given function
e a thinwith Moftriangles, 2 around all the find the optimal shape Since the edge curve are
f band width M one needs to edge curves, see figure ??. of the triangles.
f f∗h
his band can be sub-divided in elongated tubes of length proportional to M 1 ,2each of witch is
For a geometrically regular image f , that isisC outside L is one can length
2
C edges, one can however built an
mposed in two elongated triangles. The number of such triangle proof of theorem ??,the totaldesign triangles of width and legnth M
As already seen in the 2LM where
e edges in the image. A special care should be taken near edge corner approximation but weof M , whicha wavelet p
adapted triangulation that enhances so that the error in this area is also of the performance of concludes the
the tube significantly the 2
or edge crossings order
e these technicalities here. Over these tubes, the function is theorem shows that triangulation. is smoothed by an unknow
basis. The following theorem sketch the construction andsuch thewhen an image
The proof of this bounded of thus a approximation
e
||f f ||2 2 ( ) in the tubes is of the order of⇤, the triangulation should . In the on ⇤ in order to get a fast decay of the app
2 2 2
L width area( )||f ||⇤ = LM ||f ||⇤ depend complementary
e tubes c , one packs M large equilateral triangles of edge lengths approximativelythe⇤ M 1/2 .
error. To reach an error decay of O(M 2 ), in neighborhood of a contour smoothed
2
f f∗h e over ⇤ 1/4 M 1/2 and a width of order ⇤
f is C outside the edge curve, theof width ⇤, the triangle should have a length offorder such
approximation error of a linear interpolation
e||⇤( c ||f ||C 2 and thus the error satisfies??. The scale ⇤ is most of the time unknown and one thus needs an
as shown on figure
Sharp edges
gles is ||f f
Blurred edges
Figure 9.2: Approximation with finite devise 2the on aof the triangles.for a function without and with
algorithm to elements size triangulation
e
||f f ||2 = O(LM 2 ||f ||2 + ||f ||C M 2 ).
⇤
additional blurring.
M −2 s 3/ 4M −1/ 2
Theorem 2. If f is C outside a set of C2 contours, then it exists a constant C such that for
2
M −α 4the1/ 2
any M , it exists an adapted triangulation (V, T ) over which M piecewise-linear interpolation fM
s1/
satisfies M −1 triangles 1/ 4
M −12
Figure 9.2: Approximation with finite elements|| on a triangulation for a s
||f fM CM . 2 M −1/ 2
function without (9.2) with
and
additional blurring. for the
Sharp edges
Figure 9.3: Finite We give here only approximation around[todo : show an image of the tubes] Near an edges,
elements a singularity curve.
Blurred edges
Proof. a sketch of the proof.
1 2
the lengths of the triangles should be 9.4:order M ratio of triangles for the approximationM a. blurred contou
Figure of Aspect and their widths should be of order of We
2
define a thin band of width M around all the edge curves, see figure ??. Since the edge curve are
theorem shows that an adapted triangulation should balance the approximation error 1
2
Theorem, 2. If f curves. outside a set locatedcontours, from these singularities
C this band is Cbe
singularity
can of C2 far away then it exists a constant C such that for
2 sub-divided in elongated tubes of length proportional to M , each of witch is
d outside thedecomposed in two elongated triangles.that locally, an such triangle is 2LM where L is the total length
The triangles The number of optimal triangle should be aligned with the direction µ
This shows ⇥
any M , it existswhileadapted triangulation (V, T ) over which the piecewise-linear interpolation fM
e large and isotropic, an triangles that cover the edges should be stretched along the
function is thecare should be taken near edge corner or edge crossings but wewell descr
of the edges in the image. A special most regular. The local behavior of a smooth C2 image is
satisfies ignore these technicalities here. Over these tubes, the function is bounded and thus
y curves. This construction can second order by a quadratic approximation higher order the approximation
be generalized by replacing triangles by
⇥ 2 C , 2.
c primitives whose||f f ||2 2 ( ) in the tubes is of ||f order||of area(M as2 shown on ||f ||2 rightthe complementary (9.2)
error boundaries are polynomial curves M degree )||f ||⇥ = LM 2 the . In
e the f of
L ⇥
f (x + h) = f (x) + ⌅⌥xhigher order )h, h⇧ + O(||h||2 )
f, h⇧ + ⌅Hx (f
gure ??. Theof the tubes , one packs using polynomials defined on edge lengths approximatively ⌃ ⇥ M 1/2 .
adapted approximation M large equilateral triangles of M such
c
Proof. We give 2here only a sketch of the proof. [todo : show an image of the tubes] e Near an edges, 29
Since f is C outside the edge curve, the approximation error of a linear interpolation f over such
2⇥2

30. Metric Design for Anisotropic Meshing
Idea: design the metric H(x).
x e1 (x)
Local orientation: e1 (x).
Heuristic Algorithms for
2 (x)
(x) Local shape: 1 (x)/ 2 (x).
Generating Anisotropic Meshes
1
Bossen−Heckbert [1996] George−Borouchaki [1998] 30

31. Image Approximation
Garland & Heckbert, Approximation of Terrains 19
Figure 16: Mandrill original, a 200×200 raster image. Figure 17: Mandrill approximated with Gouraud
shaded triangles created by subsampling on a uniform
20×20 grid (400 vertices).
Original image
Figure 16: Mandrill original, a 200×200 raster image.
Isotropic mesh (400Gouraud
Figure 17: Mandrill approximated with
vert)
shaded triangles created by subsampling on a uniform
20×20 grid (400 vertices).
Anisotropic meshFigure 19: Mesh for the image to the left.
(400 vert)
Figure 18: Mandrill approximated with Gouraud 31

32. Image Compression
16 L. Demaret, N. Dyn, M.S. Floater, A. Iske
16 L. Demaret, N. Dyn, M.S. Floater, A. Iske
Original image
(a)
Wavelets(b)
@.25bpp
(a) (b)
(c) (d)
(c) Triangulation @.25bpp
(d)
Fig. 8. Reflex. (a) Original image of size 128 × 128. Compression at 0.251 bpp and
reconstruction by(a) Original imagePSNR 30.42 db, (d) AT∗ with PSNR 41.73 and
Fig. 8. Reflex. (b) SPIHT with of size 128 × 128. Compression at 0.251 bpp db.
2 32

33. Overview
• Riemannian Metrics.
• Riemannian Voronoi and Delaunay.
• Farthest Point Sampling.
• Anisotropic Triangulations.
• Anisotropic Delaunay Refinement.
33

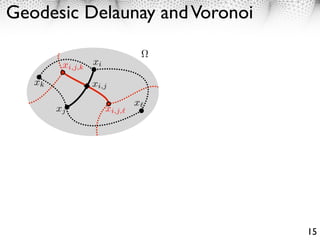
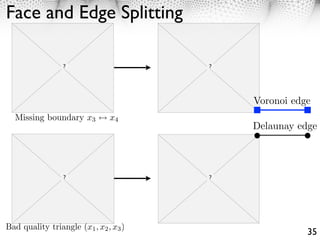
34. 105 This section, shows how several tools from computational geometry extend
Planar Domains
106 to the setting of a Riemannian metric.
107 Starting from a set of points S = {xi }m , one can define graphs and trian-
i=1
ECCV-08 submission ID1057
108 gulations that 11reflect the geometry of the Riemannian manifold. These pointsECCV
and the corresponding graphs are the basic building blocks of the algorithms for
2D Riemannian manifold: [0, 1] equipped with H(x) ⇥ R
2 2 2
.
109
perceptual grouping and planar domain meshing.
e to the boundary. A boundary sub-curve i,j is 245 245 if a point xk is located too close to the boundary.
110
S if it exists a triple point wi,k,0 i,jInsee figure 246 the boundary ⇧ encroached by xk
, the following, 246 said to be of is S if it exists a triple
nnot be part of the Delaunay triangulation, anda 247 of closedSuch ancurves. x1
assumed to be set 247 7. smooth encroached edge cannot be part of the
orithm by inserting a mid point. Similarly, triple 248 of S is automatically split by the algorithm by inserting
At least one point 248 is located on each x2
Boundaries: curve, and these boundary points segment
croach any boundary sub-curve (the sub-curve is 249 249 points are not added if they encroach any boundar
⇥ ⇧ as a set of sub-curves i P(x , x )
i,j250 250 subdivided instead).
j
⇥ = with Ω
i,j
⇥ S = {x , x }.
111
⇥
Another)
x3
he Delaunay graph DS of S is not ⇧ = ⇥i,j i,j251 251 ⇥i,j ⇤ P(xi , xjj di⇥culty is that the Delaunay graph
necessarily awith i
i,j ⇥i,j ↵ S = {xi , xj }.
ng S is not dense enough, see [7]. This is because 252 252 valid triangulation if the sampling S is not dense en
i,j
connected to only one other point of S in DS . 253 253 of some isolated point, that is connected to only
Requirement: S.
(one can have xi = xj if there is only one
Dpoint on a curve). Ωc
dd points on the Voronoi cell boundary of such a 254 254 The algorithm automatically4add points on the Vo
x
255 255 point.
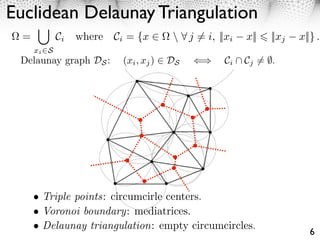
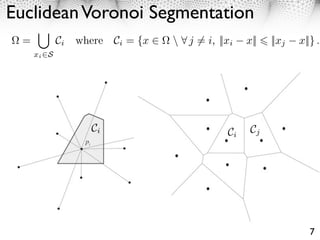
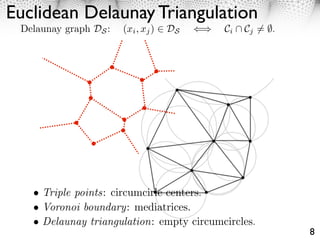
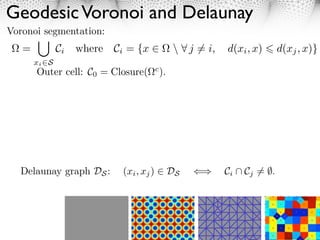
112 2.1 Delaunay and Voronoi Graphs
113 The segmentation of the domain in Riemannian Voronoi cells is
⇥
x3 = C0 Ci where Ci = {x ⇤ ⇧ j ⌅= i, d(xi , x) d(xj , x)} . (7)
xi S
x2 x1 x2 x1 x2 x1
114 The outer Voronoi cell is defined as C0 = Closure( c ).
x3
The Delaunay graph DS of S is a graph where two points are connected if
their respective Voronoi cells are adjacent
(xi , xj ) ⇤ DS ⇥ Ci ↵ Cj ⌅= ⌃.
To each Delaunay (x Bad:corresponds a double point 1,2
) D x3 encroaches wi,j
Good situationvertexpoint toedgeandi,xxjj7.⇤theS common Voronoi cell boundary , which is
aches the boundary curve ⇥ . Right:the closest x
1,2 the xi Fig. on Left: the vertex x encroaches the boundary
3 3
e (x1 , x2 ) is a Delaunay edge. does not encroach anymore because (x1 , x2 ) is a Delau
wi,j = argmin d(x, xi ).
x Ci ⌅Cj 34

35. Face and Edge Splitting
Voronoi edge
Missing boundary x3 x4
Delaunay edge
Bad quality triangle (x1 , x2 , x3 )
35

36. It extends the isotropic farthest point seeding strategy of [?] w
242
Riemannian Delaunay Refinement
Fig. 7. Left: the vertex 243 encroaches and domains with arbitrary boundaries. vertex x3
x3 metrics the boundary curve ⇥1,2 . Right: the
does not encroach anymore becauseOur ,anisotropic meshing algorithm proceeds by iteratively i
(x1 x2 ) is a Delaunay edge.
xpoint si,j,k ⇥ S to an already computed set of points S. In or
1
an anisotropic mesh with triangles of high quality with resp
x2
x2 metric, one inserts si,j,k circumradius triangle (xi , xj , xk ) w
for a Delaunay
= shortest edge
Table 2 details this algorithm. A boundshortest edge ratio the refinement to
x1
s1,2,3 circumradius to ⇥⇥ on ⇥ enforces
reach some quality criterion, while a bound U ⇥ enforces a uniform refinement to
x3
x3 s1,2,3 d(si,j,k , xi )
match some desired triangle density. ⇥(si,j,k ) = ,
min(d(xi , xj ), d(xj , xk ), d(xk , xi ))
244 which is a quantity computed for each triple point in parallel to
1. Initialization: set S with at ing propagation. In the Euclidean of , compute US(xi , xj , xk )
245 least one point on each curve domain, a triangle with
a Fast Marching. 246 of ⇥(si,j,k ) is badly shaped since its smallest angle is close to 0 .
2. Boundary enforcement: while it exists ⇥i,j extends encroached by some xk ⇤ S, angl
247 [?], this property ⌃ to an anisotropic metric H(x) if
subdivide: S ⇥ S ⌃ argmax using the inner product defined by Fast Marching.
248
U (x). Update U with a local H(x).
S S
x⇤⇤i,j
3. Triangulation enforcement: while it exists (xi , xj ) ⇤ DS with xi or xj isolated,
insert w⇥ = argmax d(xi , w).
w⇤Ci ⇧Cj
⇧
4. Select point: s ⇥ argmin ⇤(s).
s⇤ S ⌃⇥
⇧ ⇧
– If in S ⌃ {s }, s encroaches some ⇥i,j ⌃ , subdivide: S ⇥ S ⌃ argmax US (x).
x⇤⇤i,j
⇧
– Otherwise, add it: S ⇥ S ⌃ s .
Update US with a local Fast Marching.
5. Stop: while ⇤(s⇧ ) > ⇤⇧ or US (s⇧ ) > U ⇧ , go back to 2.
36

37. Isotropic vs. Anisotropic Meshing
Isotropic
Anisotropic
37

38. Examples of Anisotropic Meshing
etric dual of an anisotropic Voronoi di-
Given polygonal domain and metric tensor field M,
angulation. We describe conditions in
guaranteed to be entirely visible from
Main Result
ction 5. For the special case of two di-
ons also guarantee that the planar dual
with no inverted triangles. M is smooth with bounded
If metric tensor
nisotropic mesh. generates high- has angle < 20° as
ible an algorithm that no triangle
derivatives,
isotropic meshes by refi ning anpoint in the triangle.
measured by any aniso-
nforce the conditions that guarantee that
ndgenerate any poor-quality elements
to remove anisotropic mesh.
38

39. Bonus
• Centroidal Tesselations
39

40. Centroidal Tesselation
A ⇥ Rn , Euclidean center of gravity: g(A) = argmin A
||x y||2 dy.
x
A M, geodesic center of gravity: gM (A) = argmin A
dM (x, y)2 dy
x
Sampling {xi }m , Voronoi tessellation VoronoiM ({xi }i ) = {Vi }m .
i=1 i=1
Centroidal tessellation i, xi = gM (Vi ), local minimizer of
m ⇥
E({xi }, {Vi }i ) = dM (xi , y)2 dy.
i=1 Vi
⇥
EA (x) = dM (x, y) dy
2
=⇤ ⌅x EA = dM (x, y)nx (y)dy
A A
⇥
nx (y)
1. Initialize: {xi }i random.
Lloyd-Max
x
2. Update regions: ⇥ i, {Vi }i VoronoiM ({xi }i ).
y
3. Update centers: ⇥ i, xi gM (Vi ).
4. Stop: while not converged, go back to 2.
40

41. Centroidal Tesselations of the Plane
uniform
#iterations
adaptive
= Delaunay = Voronoi
41

42. Centroidal Tesselations of Surfaces
#iterations
42