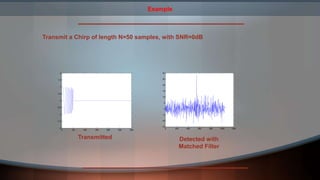
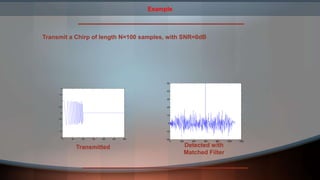
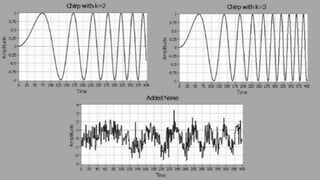
The document describes matched filter detection using LabVIEW. It involves generating a chirp signal, adding noise to create a noisy waveform, and then using a matched filter to detect the chirp signal in the presence of noise. Specifically, it generates a chirp signal, adds white Gaussian noise, and uses a filter with an impulse response that is the time-reversed version of the chirp signal to maximize the signal-to-noise ratio and detect the chirp signal in the noisy waveform. It provides examples detecting chirp signals of different lengths in the presence of noise.

1. Matched Filter Detection
Using lab view

2. Objectives(Tasks)
Generation of
chrip signal
Generation
of noisy
wave form
Matched
filter
detection
• Generation of chirp signal
• Generation of noisy wave form
• Matched filter detection

3. 2
Matched Filter
• Detection of pulse in presence of additive noise
Receiver knows what pulse shape it is looking for
Channel memory ignored (assumed compensated by other means, e.g. channel equalizer in
receiver)
Additive white Gaussian noise
(AWGN) with zero mean and
variance N0 /2
g(t)
Pulse
signal
w(t)
x(t)
h(t)
y(t)
t = T
y(T)
Matched
filter
y t g t h t w t h t
( )  ( )* ( ) 
( )* ( )
0 g t n t
 
( ) ( )
T is pulse
period

4. 13 - 4
Matched Filter
• Given transmitter pulse shape g(t) of duration T, matched filter
is given by hopt(t) = k g*(T-t) for all k
Duration and shape of impulse response of the optimal filter is
determined by pulse shape g(t)
hopt(t) is scaled, time-reversed, and shifted version of g(t)
• Optimal filter maximizes peak pulse SNR
SNR
2


E
b 
g t dt
G f df
    | ( ) |
 
max 2
| ( ) |
2
0
2
N
 0
2
0

N
N
Does not depend on pulse shape g(t)
Proportional to signal energy (energy per bit) Eb
Inversely proportional to power spectral density of noise

5. Typical Application: Radar
Send a Pulse…
] [ns
n
… and receive it back with noise, distortion …
] [ny
n
0 n
N
Problem: estimate the time delay , ie detect when we receive it. 0 n

6. Use Inner Product
“Slide” the pulse s[n] over the received signal and see when
the inner product is maximum:
s[]
[ ]  [ 
] * [ ]

y[]

0 n
N
n



1
0
N
ys r n y n s

 
0 r [n] 0, if n n ys  

7. Use Inner Product
“Slide” the pulse x[n] over the received signal and see when
the inner product is maximum:

* [ ] [ ] [ ]
if 0 nnMAX s n y n r
0 n  
s[]

y[]

N
N
ys   

1
0

 

8. Matched Filter
Take the expression

1
*
 
 
r n y n s
[ ] [ ] [ ]
0

* * *
s N y n N s y n s y n
[ 1] [ 1] ... [1] [ 1] [0] [ ]
N
n
ys
       
Compare this, with the output of the following FIR Filter
rˆ[n]  h[0]y[n]... h[1]y[n 1] h[N 1]y[n  N 1]
Then
y[n] h[n]
rˆ[n]  r [n  N 1] ys
[ ] [ 1 ], 0,..., 1 * h n  s N   n n  N 

9. Matched Filter
This Filter is called a Matched Filter
y[n] rˆ[n]
] [nh
[ ] [ 1 ], 0,..., 1 * h n  s N   n n  N 
The output is maximum when
rˆ[n]  r [n  N 1] ys
0 n  N 1 n
1 0 i.e. n  n  N 

10. Example
We transmit the pulse s [ n ] , n  0 , . . . , N  1 shown below, with
length N  20
0 2 4 6 8 10 12 14 16 18 20
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
] [ns
0 20 40 60 80 100 120 140 160 180 200
12
10
8
6
4
2
0
-2
-4
-6
1.5 ] [ny
1
0.5
0
-0.5
-1
-1.5
0 20 40 60 80 100 120 140 160 180
-2
y[n] rˆ[n]
h[n]
[ ] [ 1 ], 0,..., 1 * h n  s N   n n  N 
Received signal:
Max at n=119
119 20 1 100 0 n    

11. Example: Chirp
r [n], n  49,...,49 ss
0 5 10 15 20 25 30 35 40 45 50
s[n],n  0,...,49
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-0.6
-0.8
-1
30
25
20
15
10
5
0
-5
-10
-50 -40 -30 -20 -10 0 10 20 30 40 50
s=chirp(0:49,0,49,0.1)

12. Example
Transmit a Chirp of length N=50 samples, with SNR=0dB
0 50 100 150 200 250 300
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0 200 400 600 800 1000 1200
30
25
20
15
10
5
0
-5
-10
-15
Transmitted Detected with
Matched Filter

13. Example
Transmit a Chirp of length N=100 samples, with SNR=0dB
0 50 100 150 200 250 300
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0 200 400 600 800 1000 1200
50
40
30
20
10
0
-10
-20
Transmitted Detected with
Matched Filter