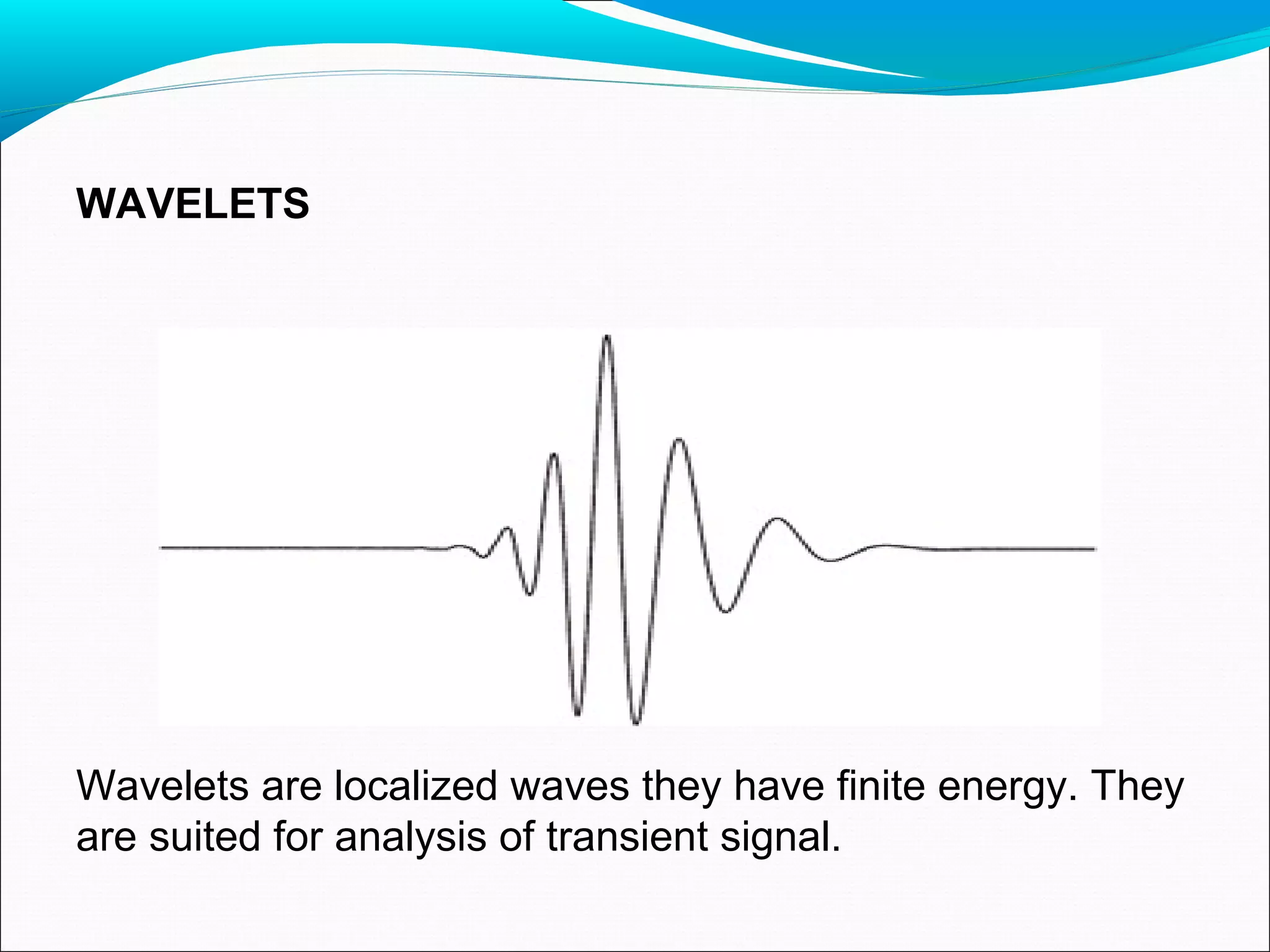
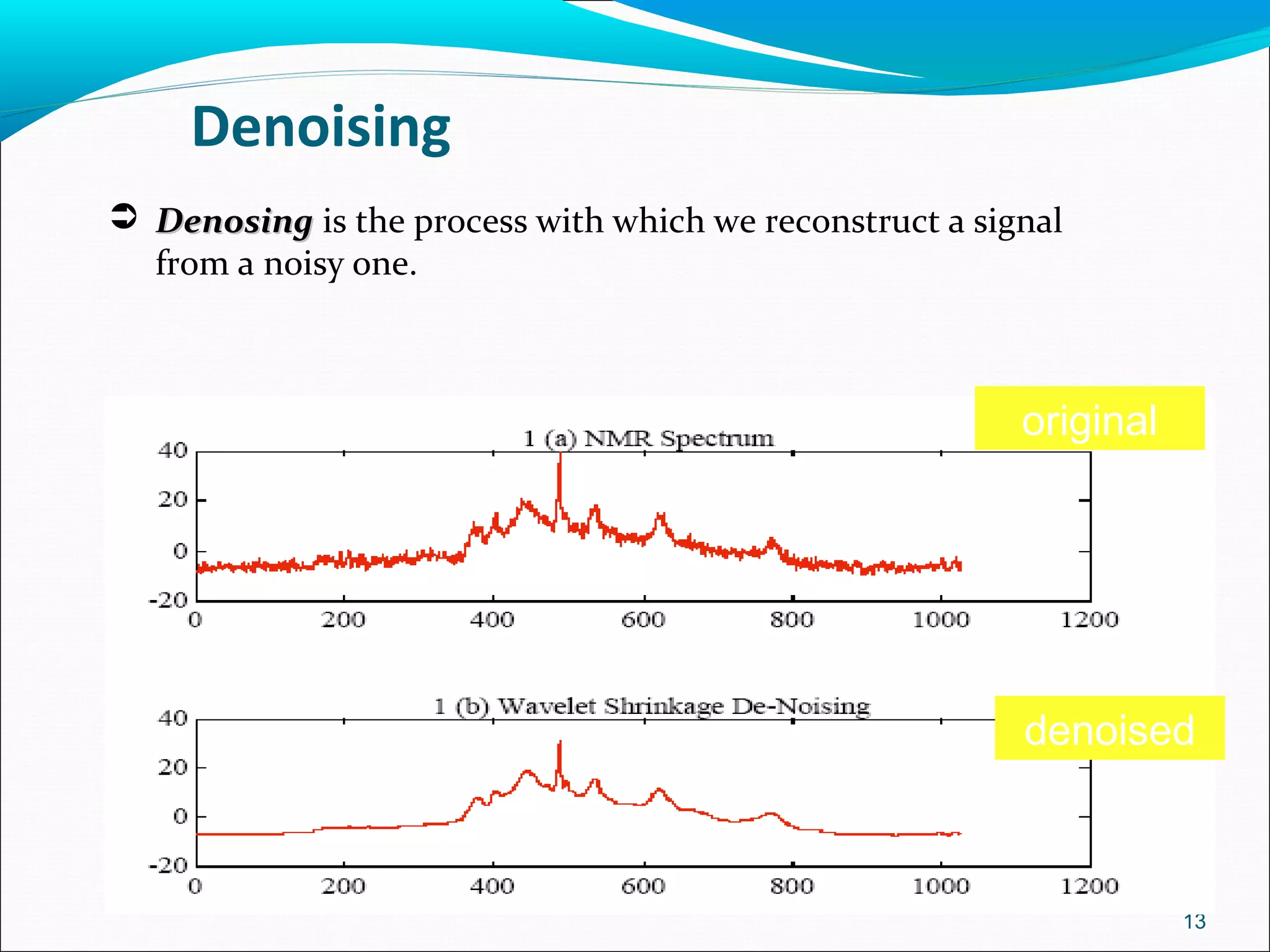
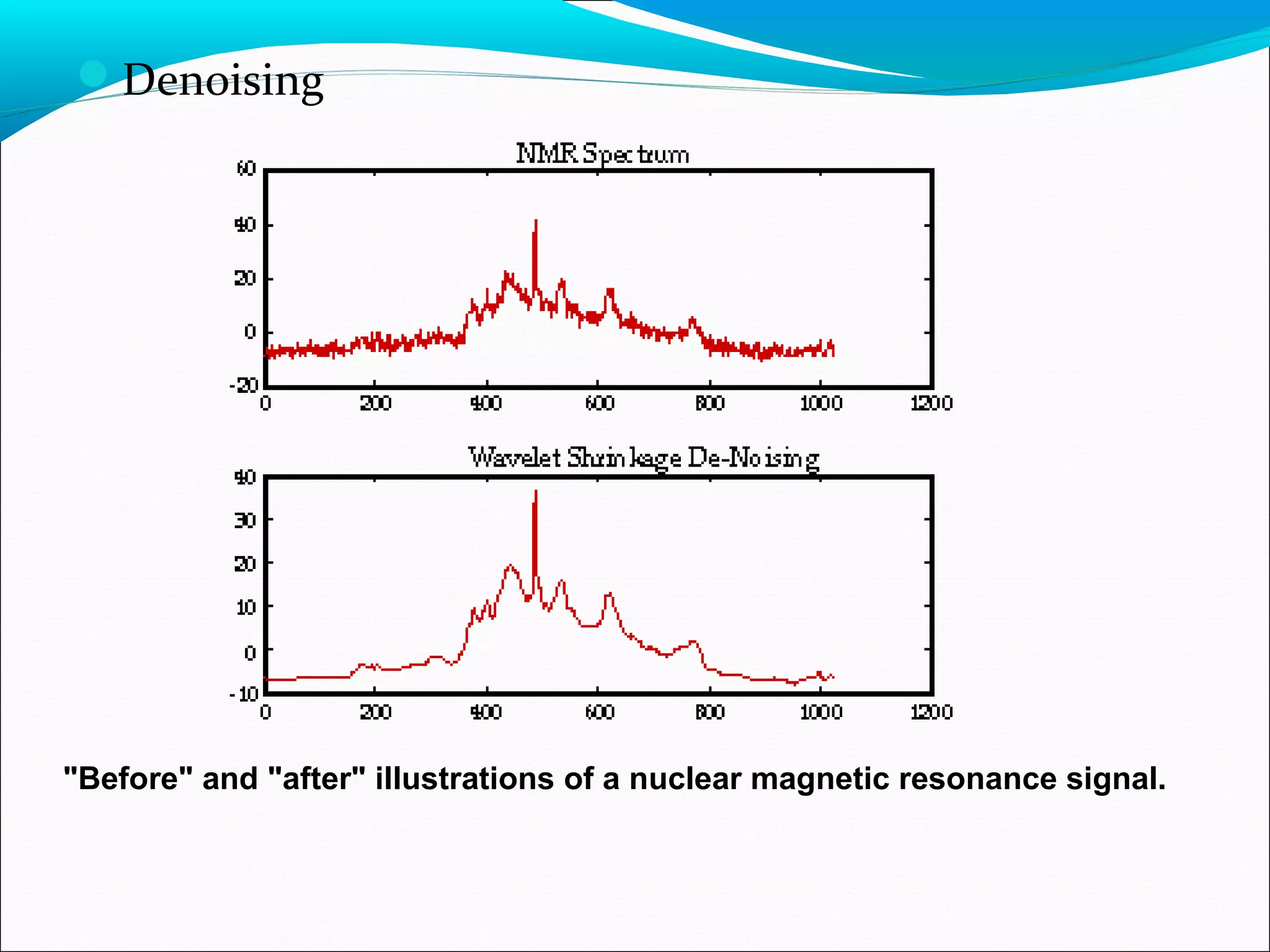
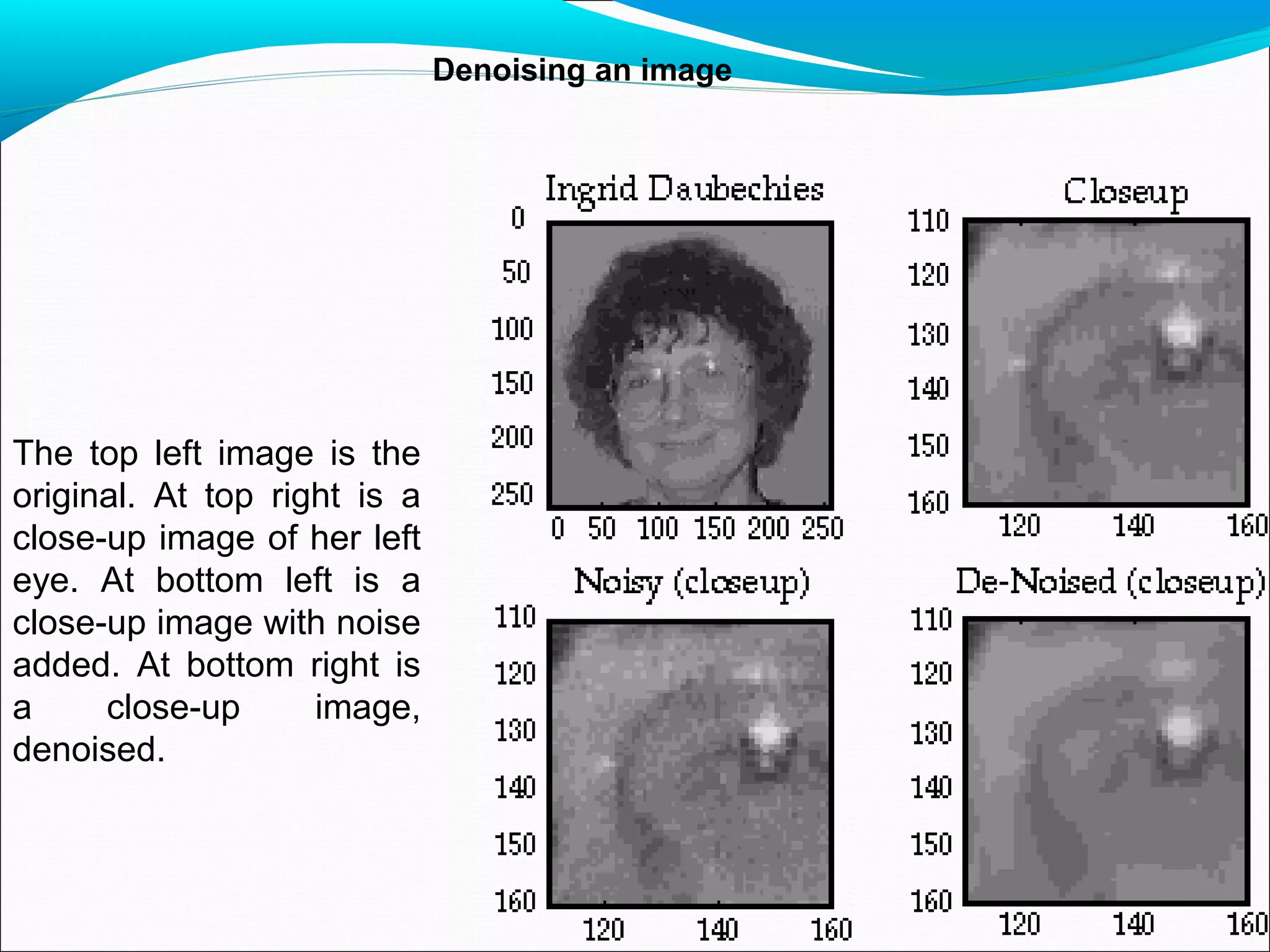
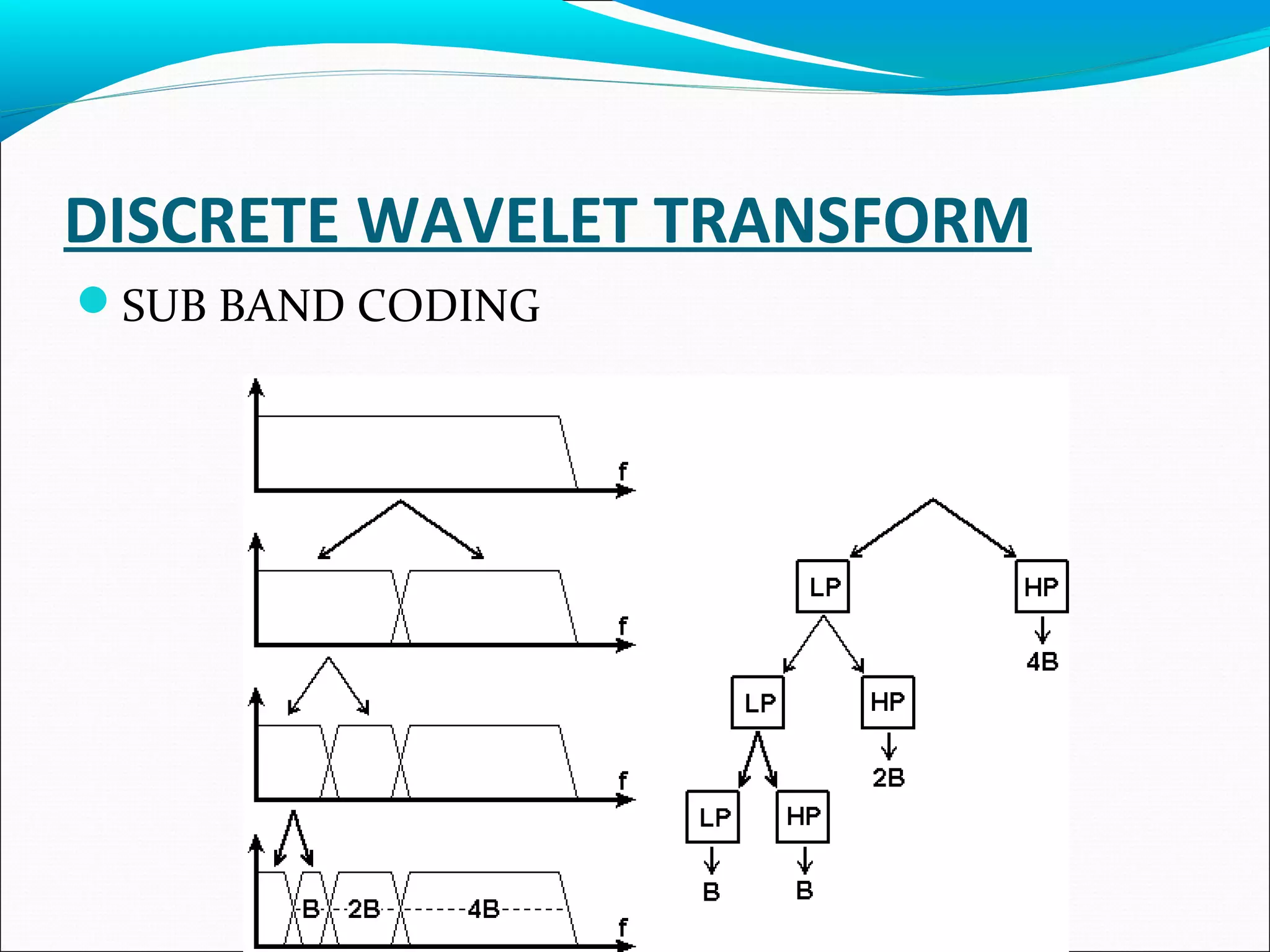
This document discusses using wavelet transforms for denoising images. It begins with an introduction to transforms and why wavelet transforms are useful compared to Fourier transforms. It then covers continuous and discrete wavelet transforms, different wavelet families, and multi-resolution analysis using filter banks. The document analyzes denoising performance using peak signal-to-noise ratio and applies wavelet transforms to applications like numerical analysis and signal processing. In conclusion, wavelet transforms provide multiresolution representation making them preferable to Fourier transforms for tasks like denoising.

1. DENOISING OF IMAGE USINGDENOISING OF IMAGE USING
WAVELETSWAVELETS
By- Asim Sagheer, Ravi Bhushan, Qutub Zeeshan

2. CONTENTS
INTRODUCTION
WHY WAVELET TRANSFORM
WAVELETS
CONTINUOUS WAVELET TRANSFORM
DISCRETE WAVELET TRANSFORM
ANALYSIS
APPLICATIONS
CONCLUSION

3. INTRODUCTION
WHAT IS TRANSFORM?
- Transform of a signal is just another form of
representing the signal. It does not change the
information content present.
WHY TRANSFORM?
- Mathematical transform are applied to
signal to obtain further information which is not
present in raw signal

4. WHY WAVELET TRANSFORM
FOURIER TRANSFORM
SHORT TIME FOURIER TRANSFORM
WAVELET TRANSFORM

5. FOURIER TRANSFORM:
Fourier Transform of a time domain signal gives
frequency domain representation.
LIMITATION OF FOURIER TRANSFORM:
When we are in time domain fourier transform will
not give information regarding frequency and when
we are in frequency domain it will not provide
information regarding time.

6. ULTIMATE SOLUTION:
WAVELET TRANSFORM
Wavelet transform provides time frequency
representation simultaneously.
It provides variable resolution as follows:
“At high frequency wavelet transform gives good time
resolution and poor frequency resolution”
“At low frequency wavelet transform gives good
frequency resolution and poor time resolution”.

7. SHORT TIME FOURIER TRANSFORM
Short time fourier transform provides time frequency
representation of a signal.
UNCERTAINITY PRINCIPLE
“Which states that we cannot exactly know what
frequency exist at what time instance but we can know
only what frequency band exists at what time.”
 DECOMPOSITION OF SIGNALDECOMPOSITION OF SIGNAL
0-500 Hz
500-1000Hz
250-500 Hz0-250 Hz
0-125 Hz 125-250 Hz

8. WAVE
Demonstration of wave
A wave is a periodic oscillating function that travels through space and matter
accompanied by a transfer of energy.

9. Wavelets are localized waves they have finite energy. They
are suited for analysis of transient signal.
WAVELETS

10. Image Pyramids
Approximation pyramids
Predictive residual pyramids
MRA
10
N*N
N/2*N/2
N/4*N/4
N/8*N/8
N*N
N/2*N/2
N/4*N/4
NN/8*N/8
/8*N/8

11. Noise Model
Image Noising:-
Image noise is the random variation of brightness or
color information in images produced by the sensor
and circuitry of a scanner or digital camera. Image
noise can also originate in film grain and in the
unavoidable shot noise of an ideal photon detector

12. Types of Noising Model
Amplifier Noise(Gaussian Noise)
Salt and paper Noise
Shot Noise(Poisson Noise)
Speckle Noise

13. February 13, 2015
13
Denoising
 DenosingDenosing is the process with which we reconstruct a signal
from a noisy one.
original
denoised

14. Denoising
"Before" and "after" illustrations of a nuclear magnetic resonance signal.

15. Denoising an image
The top left image is the
original. At top right is a
close-up image of her left
eye. At bottom left is a
close-up image with noise
added. At bottom right is
a close-up image,
denoised.

16. BLOCK DIAGRAM

18. PROPERTIES OF WAVELETS:
Consider a real or complex value continuous time
function (t) with the following properties
---- (1)
In equation (1) ( ) stands for Fourier transform of (t) .
The admissibility condition implies that the Fourier transform of (t)
vanishes at the zero frequency i.e
A zero at the zero frequency also means that the average value of
the wavelet in the time domain must be zero
(t) must be oscillatory. In other words (t) must be a wave.

19. Shifting operation gives time represntation of the
spectral component.
Scaling operation gives frequency.

20. WAVELET FAMILIES
(a) Haar Wavelet (b) Daubechies4 Wavelet
(c)Coiflet1 Wavelet

21. (d) Symlet2 Wavelet (e) MexicanHat Wavelet
(f) Meyer Wavelet (g) Morlet Wavelet

22. THE CONTINUOUS WAVELET TRANSFORM
where * denotes complex conjugation of
f(t) is the signal to be analyzed
S is the scaling factor
is the translation factor
Inverse wavelet transform is given by

23. DISCRETE WAVELET TRANSFORM
SUB BAND CODING

24. MULTIRESOLUTION ANALYSIS USING FILTER
BANK
Three-level wavelet decomposition tree
Three-level wavelet reconstruction tree.

25. CONDITION FOR PERFECT
RECONSTRUCTION
To achieve perfect reconstruction analysis and synthesis
filter have to satisfy following conditions:G0 (-z) G1 (z) + H0 (-z). H1 (z) = 0 -------- (1)
G0 (z) G1 (z) + H0 (z). H1 (z) = 2z-d ------- (2)
Where G0(z) be the low pass analysis filter,
G1(z) be the low pass synthesis filter,
H0(z) be the high pass analysis filter,
H1(z) be the high pass synthesis filter.
First condition implies that reconstruction is aliasing free
Second condition implies that amplitude distortion has amplitude of
unity

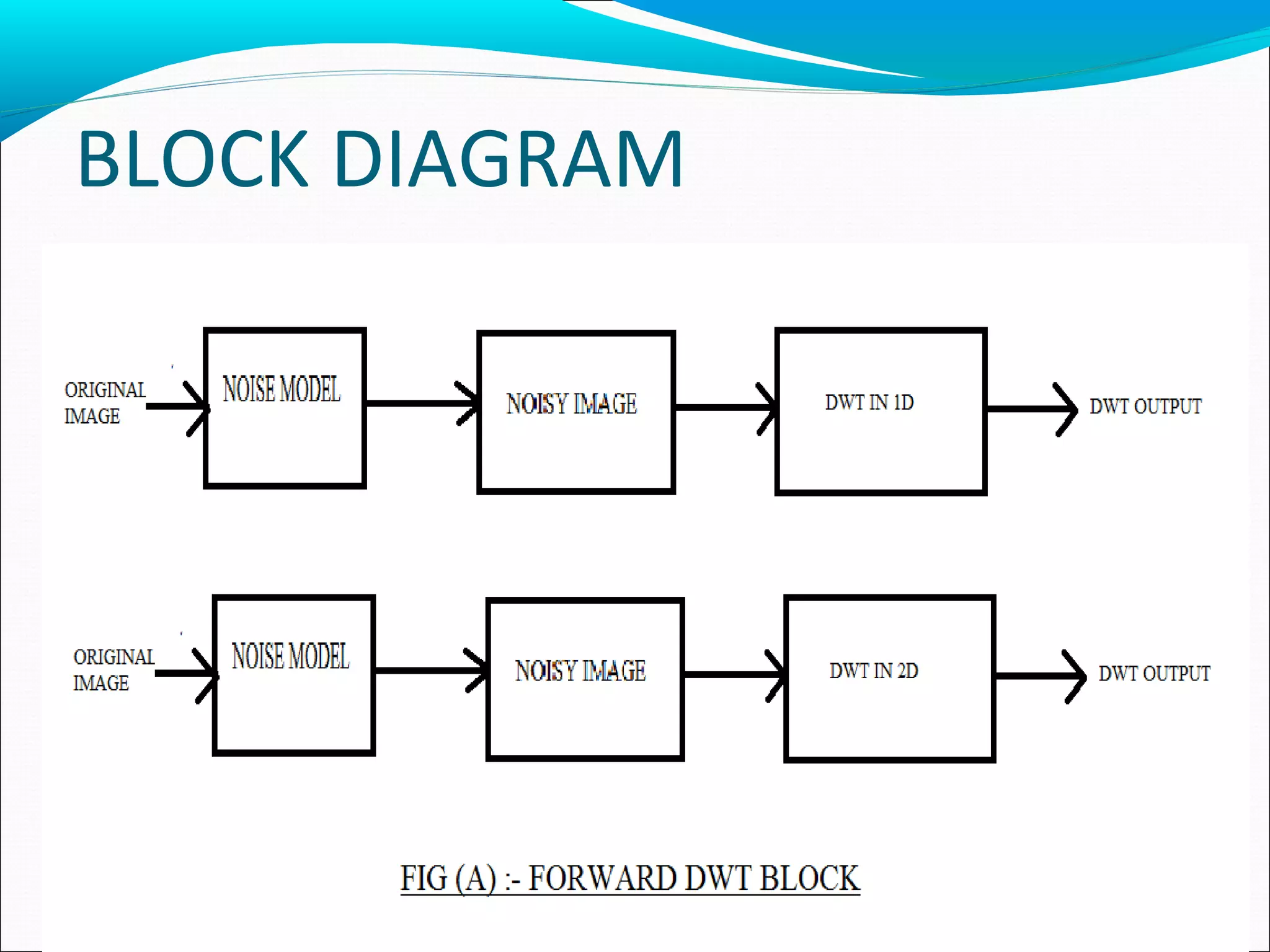
26. 1D fast wavelet transforms
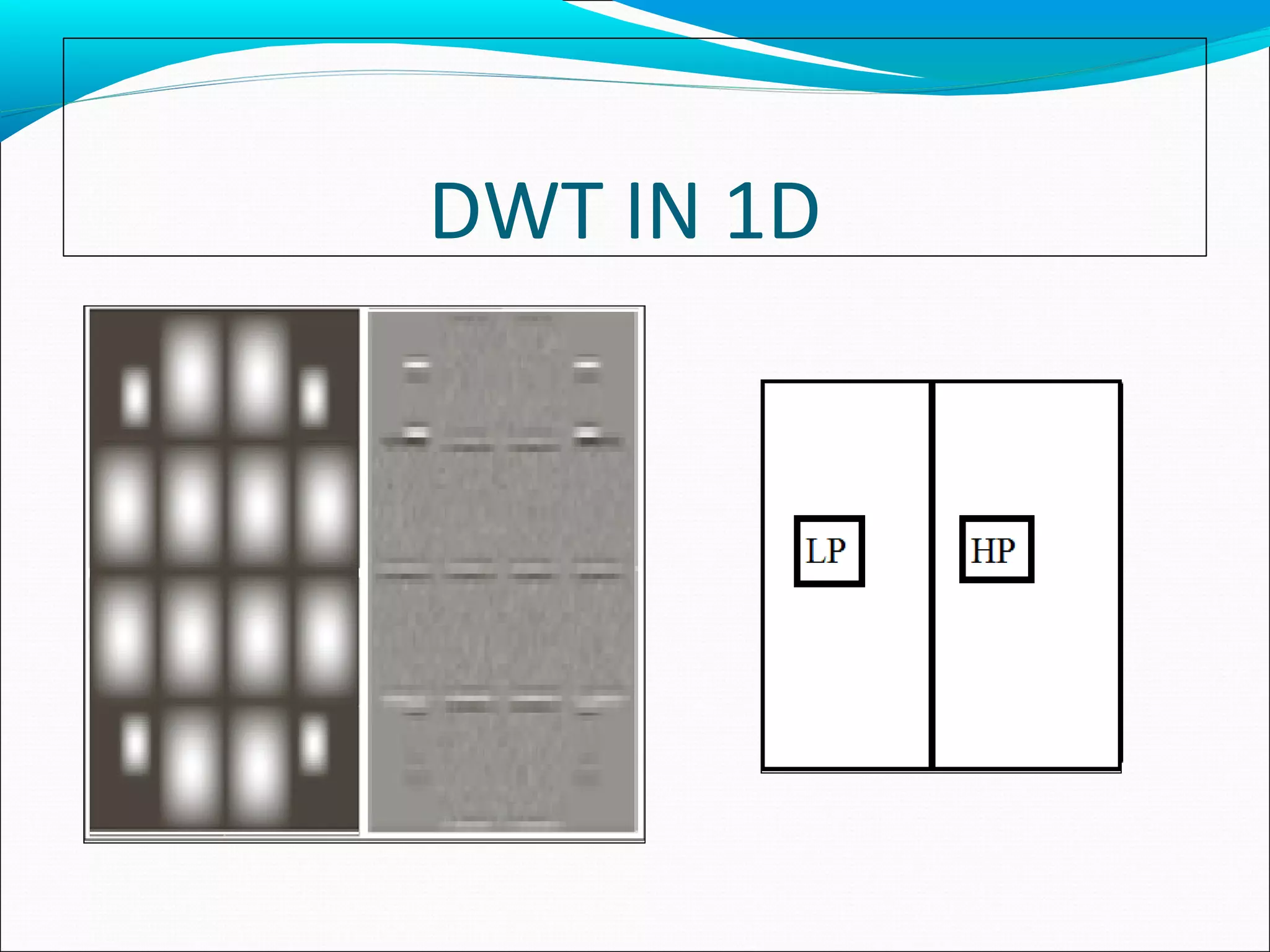
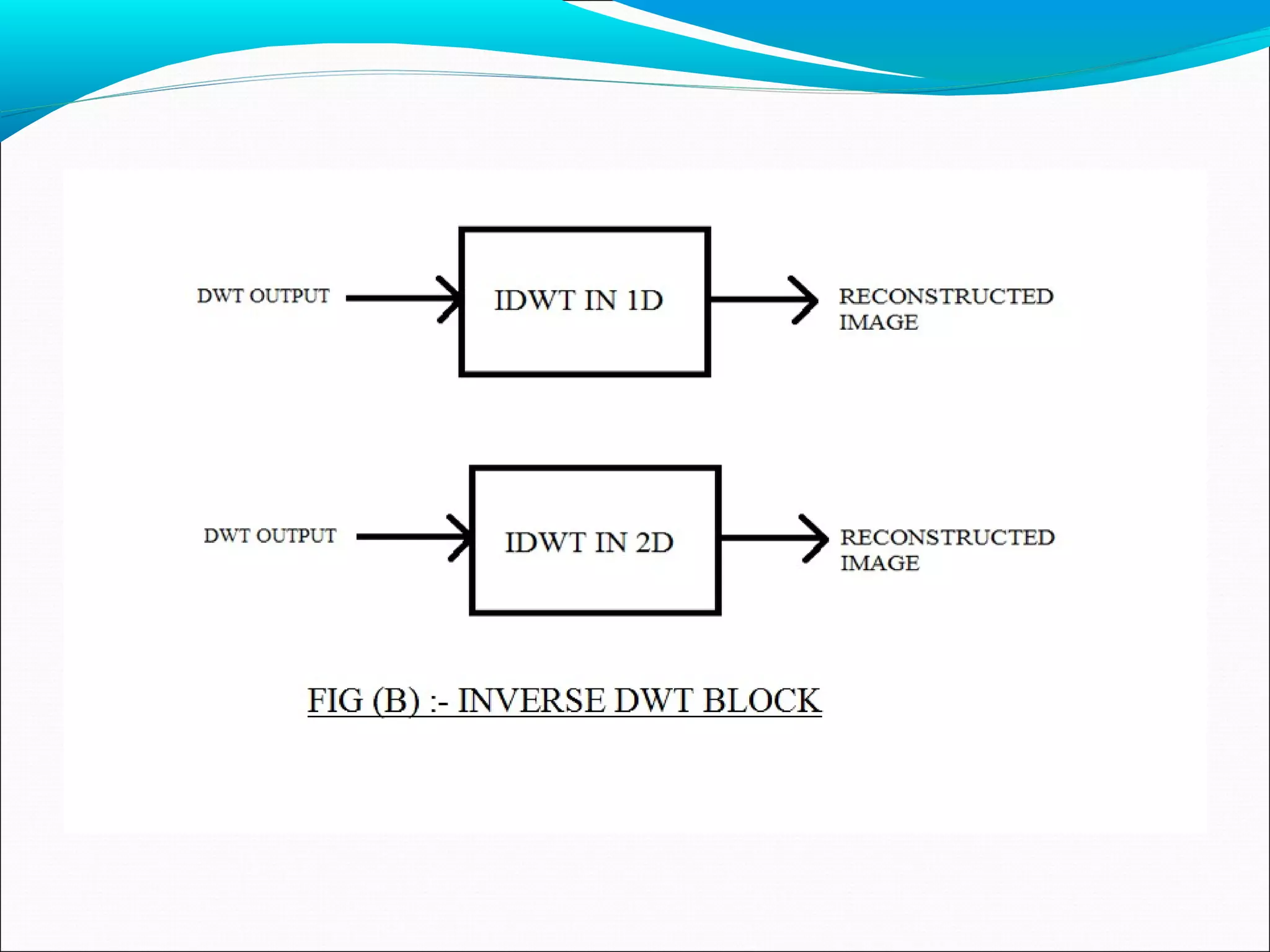
Due to the separable properties, we can apply 1D FWT.
DWT IN 1D
26
[1]

27. 2D fast wavelet transforms
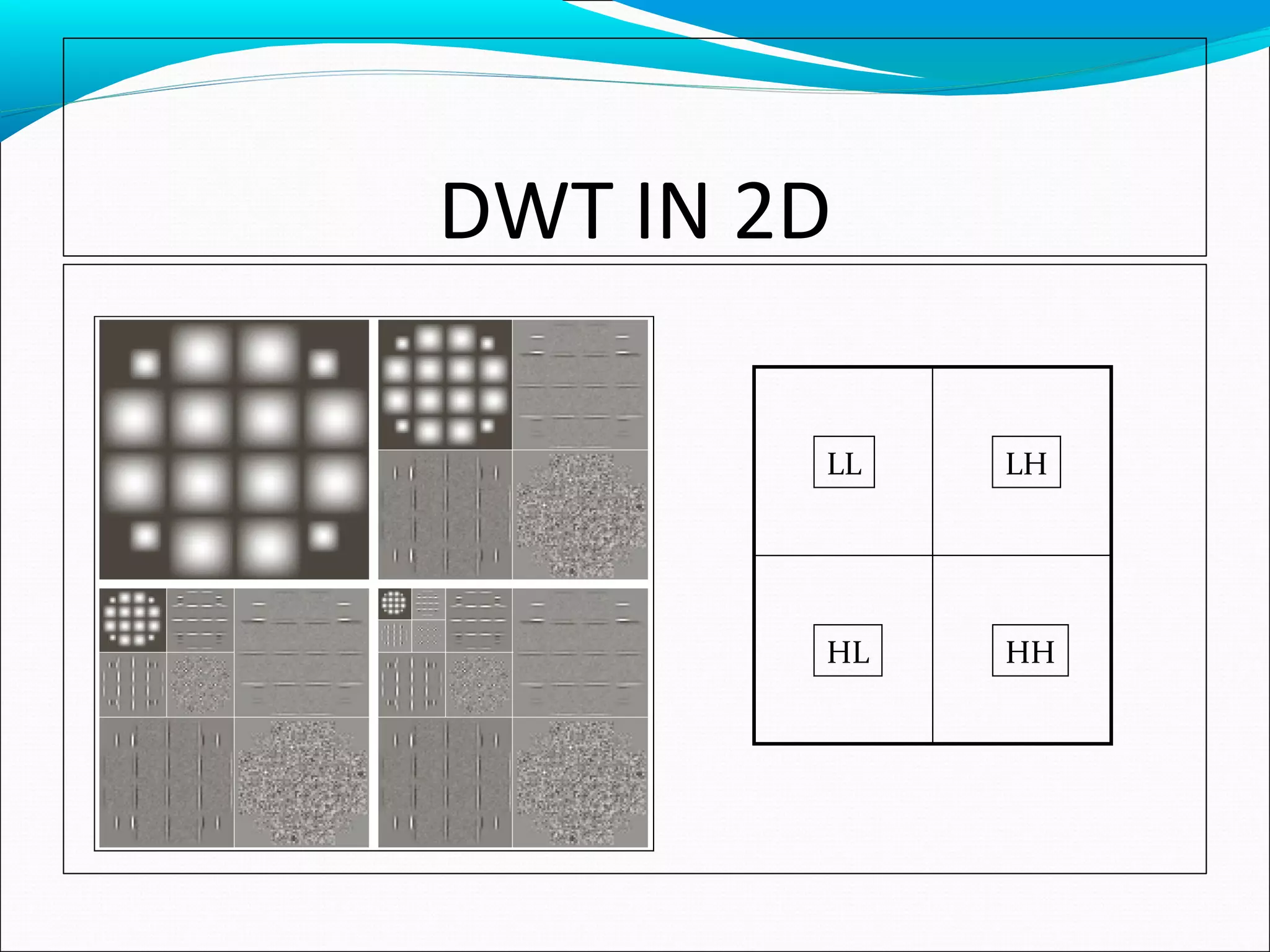
Due to the separable properties, we can apply 1D FWT to
do 2D DWTs.
DWT IN 2D
27
[1]

28. DWT IN 1D

29. – An example
DWT IN 2D
LL LH
HL HH

30. ANALYSIS
The PSNR block computes the peak signal-to-noise ratio, in
decibels, between two images. This ratio is often used as a
quality measurement between the original and a
compressed image. The higher the PSNR, the better the
quality of the compressed, or reconstructed image.
The Mean Square Error (MSE) and the Peak Signal to Noise
Ratio (PSNR) are the two error metrics used to compare
image compression quality. The MSE represents the
cumulative squared error between the compressed and the
original image, whereas PSNR represents a measure of the
peak error. The lower the value of MSE, the lower the error.

31. To compute the PSNR, the block first calculates the mean-
squared error using the following equation:
In the previous equation, M and N are the number of rows
and columns in the input images, respectively. Then the
block computes the PSNR using the following equation:
In the previous equation, R is the maximum fluctuation in
the input image data type. For example, if the input image
has a double-precision floating-point data type, then R is 1. If
it has an 8-bit unsigned integer data type, R is 255, etc.

32. EXAMPLE

33. APPLICATIONS

35. APPLICATIONS
1. Numerical Analysis
2. Signal Analysis
3. Control Applications
4. Audio Applications

36. CONCLUSION
Fourier transform provided information regarding
frequency.
Short time fourier transform gives only constant
resolution.
So, wavelet transform is preferred over fourier transform
and short time fourier transform since it provided
multiresolution.

37. REFERENCES
 Wavelet Transform, Introduction to Theory and
Applications, By Raghaveer M.Rao Ajit.S., Bopardikar
 Digital Image Processing, 2nd edition,
Rafael.C.Gonzalez , Richard E.Woods.
 http://www.amara.com/ieeewave/iw_ref.html#ten.
 http://www.thewavelet tutorial by ROBI Polikar.htm

38. THANK YOU
For quires: asimsagheer@gmail.com