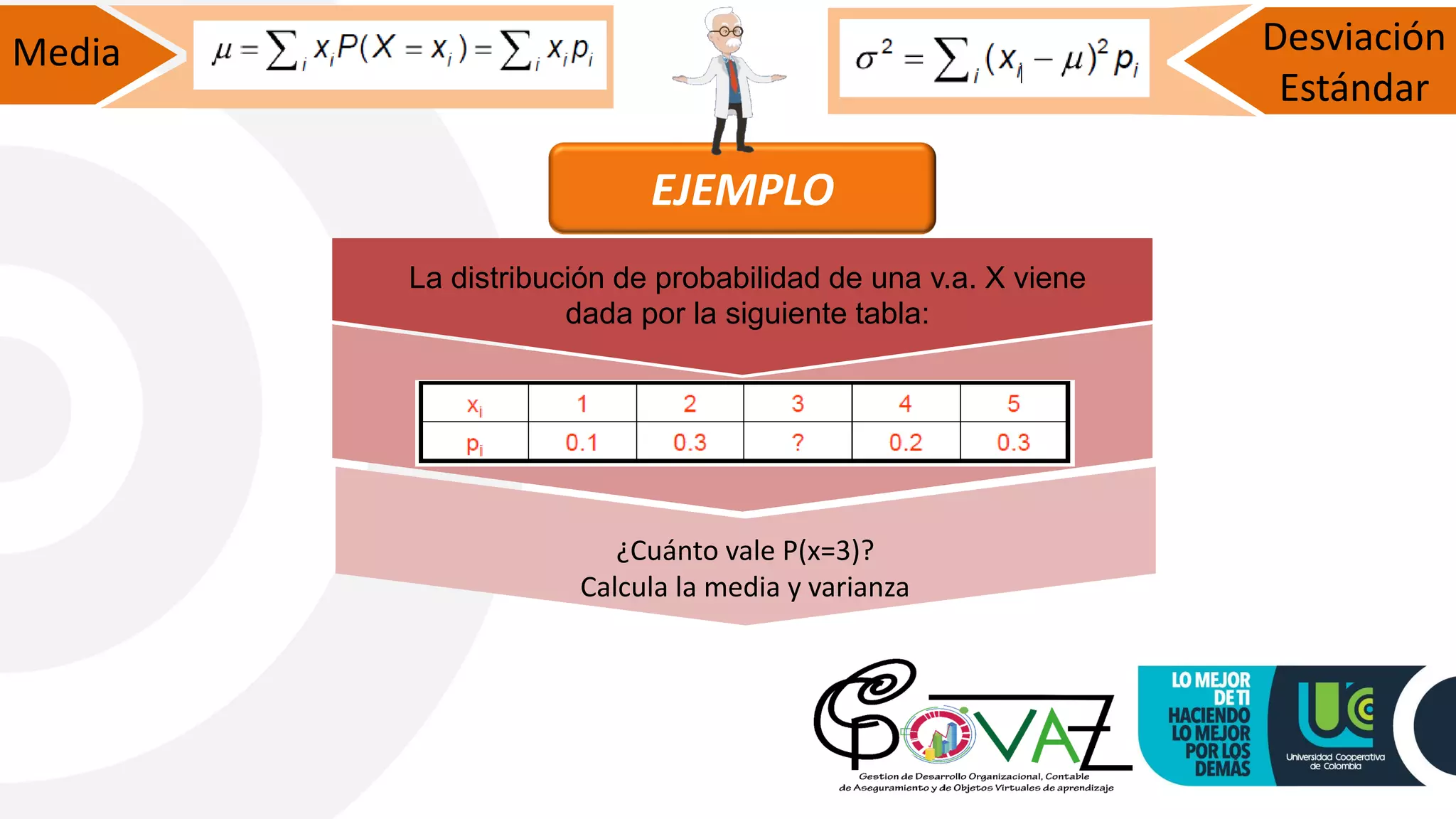
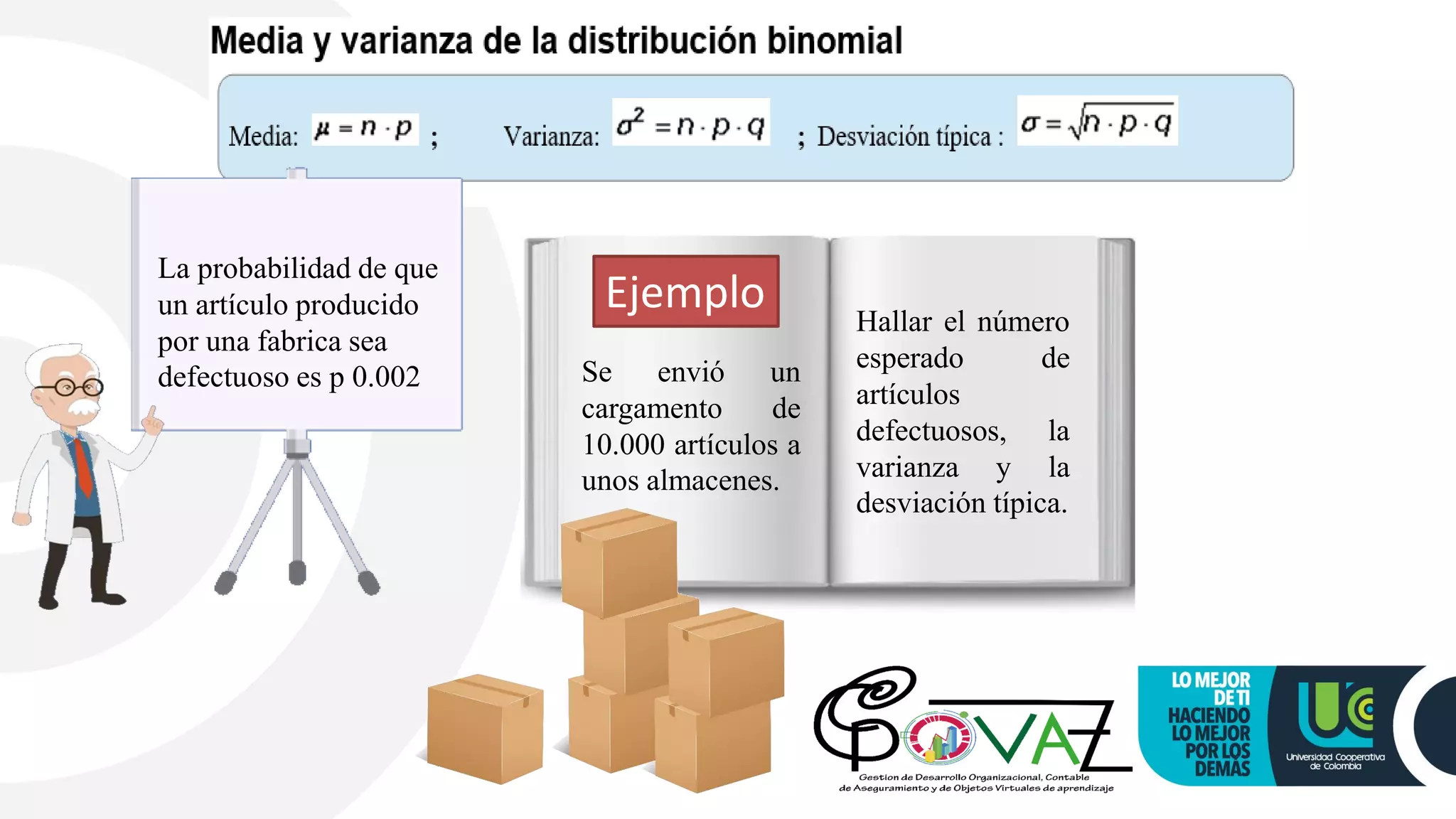
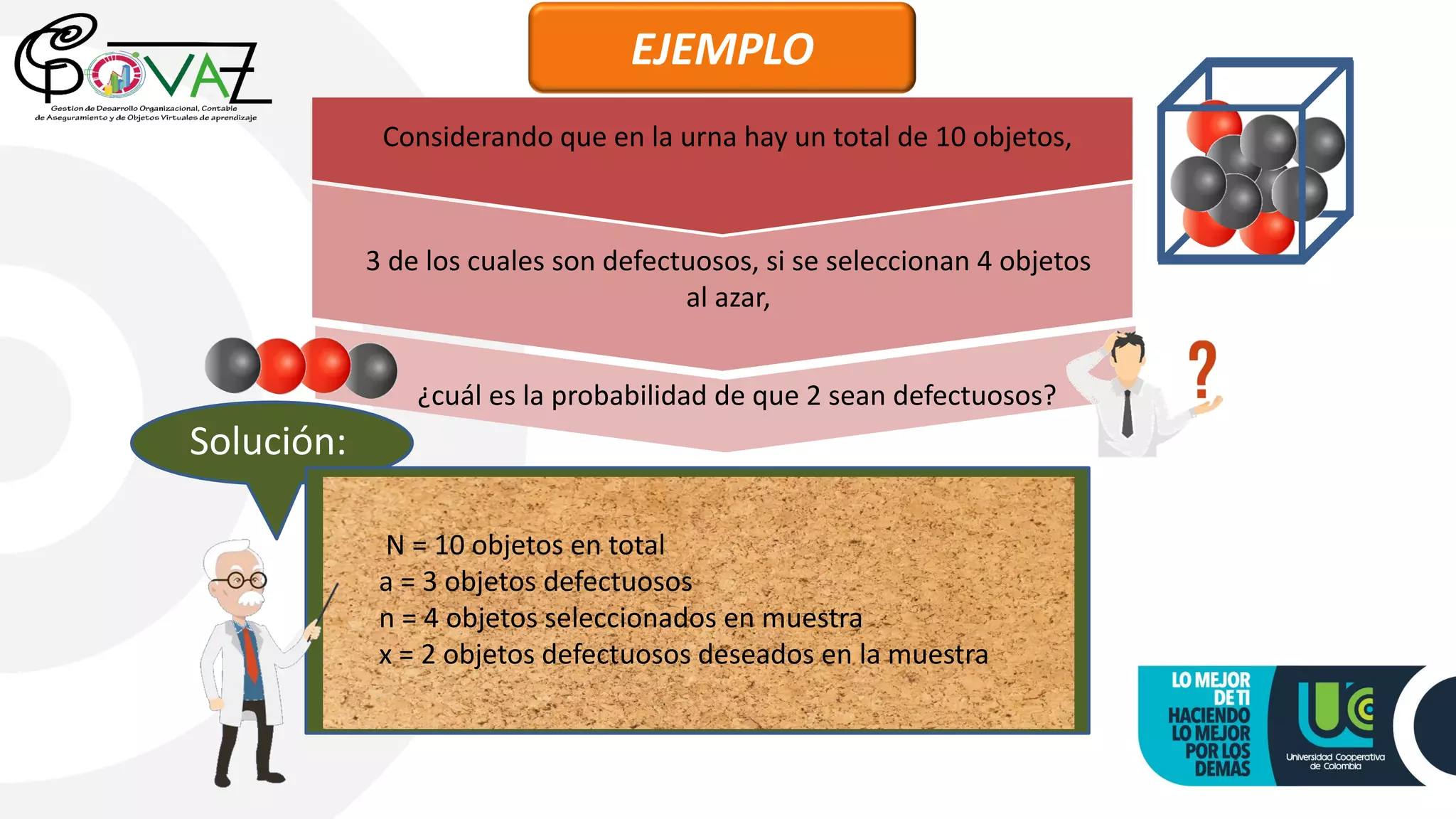
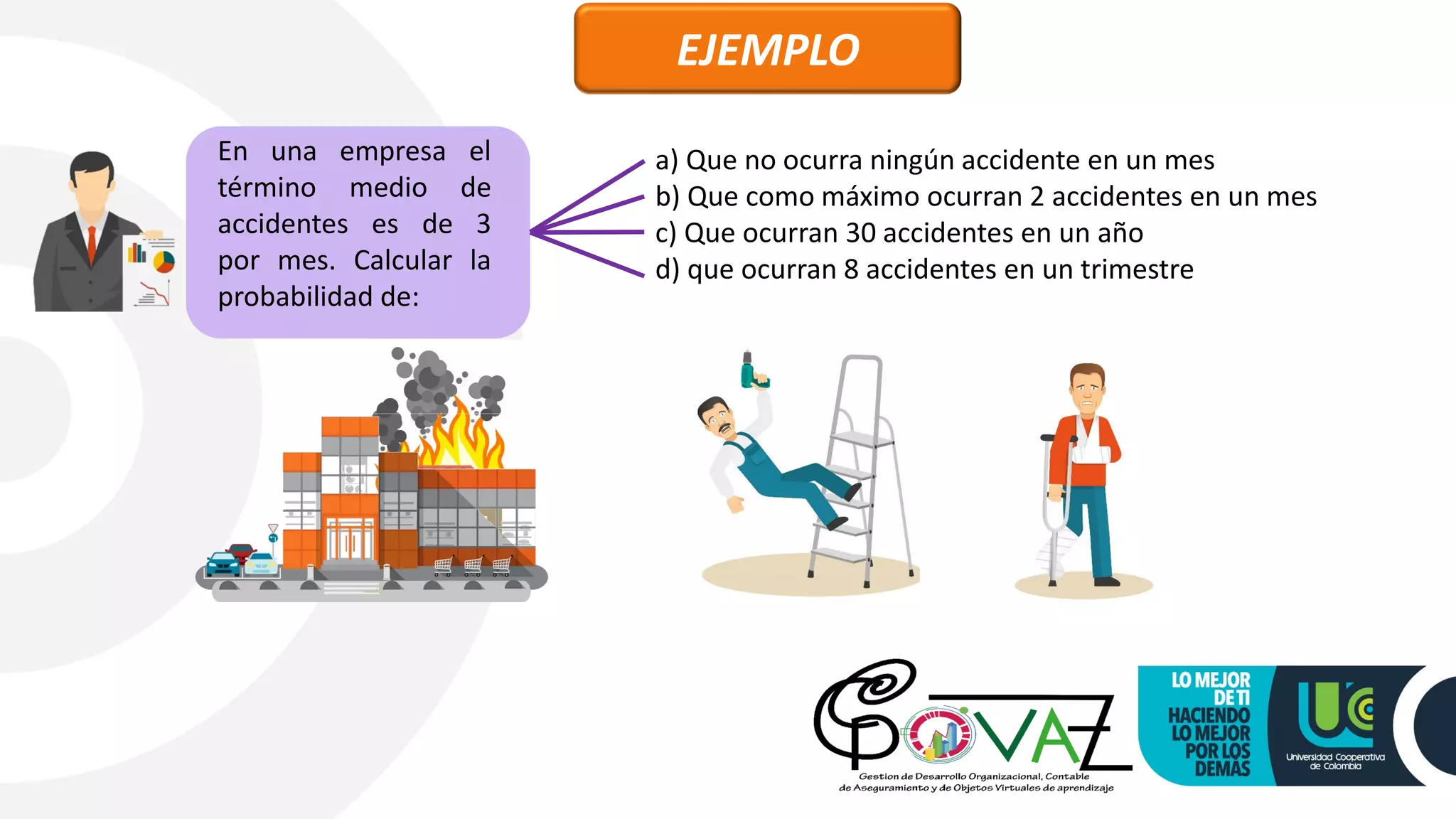
This document discusses probability models and distributions. It introduces probability functions and tables that show the values a discrete random variable can take and their corresponding probabilities. It then discusses measures like mean and standard deviation. Specific probability distributions covered include binomial, hypergeometric, Poisson, exponential and normal. Examples are provided to illustrate calculating probabilities using these distributions for scenarios involving things like the number of defective items, number of people alive after a certain time, and number of accidents occurring.

1. “Modelos probabilisticos”
Dr. Jorge Alejandro Obando Bastidas

2. Función de
probabilidad
Los valores que toma una v.a. discreta X y sus correspondientes
probabilidades suelen disponerse en una tabla con dos filas o dos
columnas llamada tabla de distribución de probabilidad:
Toda función de probabilidad
se verifica que
P1 + P2 + P3 + …. + Pn = 1

3. Media Desviación
Estándar
La distribución de probabilidad de una v.a. X viene
dada por la siguiente tabla:
¿Cuánto vale P(x=3)?
Calcula la media y varianza
EJEMPLO

4. Variables
Discretas
Binomial Hipergeometrica Poisson
Continuas
Exponencial Normal

5. En cada prueba del experimento sólo son posibles dos
resultados: el suceso A (éxito) y su contrario
P éxito es grande
La distribución
binomial
1
2
3
4
5
La probabilidad del suceso A es constante, es
decir, que no varía de una prueba a otra. Se
representa por p.
El resultado obtenido en cada prueba es independiente
de los resultados obtenidos anteriormente.
Las muestras son pequeñas
Modelo
matemático

6. La última novela de un autor ha tenido un gran éxito, hasta
el punto de que el 80% de los lectores ya la han leído.
¿Cuál es la probabilidad de que en el grupo hayan leído
la novela 2 personas?¿Y como máximo 2?
EJEMPLO
Si un grupo de 4 amigos son aficionados a la lectura:

7. Se envió un
cargamento de
10.000 artículos a
unos almacenes.
Hallar el número
esperado de
artículos
defectuosos, la
varianza y la
desviación típica.
La probabilidad de que
un artículo producido
por una fabrica sea
defectuoso es p 0.002
Ejemplo

8. Un agente de seguros vende pólizas a cinco personas de la
misma edad y que disfrutan de buena salud.
Hállese la probabilidad de que, transcurridos 30 años, vivan:
1. Las cinco personas. 2.Al menos tres personas.
3.Exactamente dos personas.
EJEMPLO
Según las tablas actuales, la probabilidad de que una
persona en estas condiciones viva 30 años o más es 2/3.

9. Distribución discreta
que modela el No.
de eventos
Distribución
Hipergeometrica
(es un evento o
un no evento)
En una muestra
de tamaño fijo
Al conocer el No.
total de elementos
en la población.
Proveniente
de la muestra
Cada elemento con 2
resultados posibles

10. Considerando que en la urna hay un total de 10 objetos,
¿cuál es la probabilidad de que 2 sean defectuosos?
EJEMPLO
3 de los cuales son defectuosos, si se seleccionan 4 objetos
al azar,
Solución:
N = 10 objetos en total
a = 3 objetos defectuosos
n = 4 objetos seleccionados en muestra
x = 2 objetos defectuosos deseados en la muestra

11. Distribución de
Poisson
La variable
aleatoria discreta
X
Tiene valores
posibles que son:
0,1,2…
Tiene
distribución
Poisson con
parámetro
𝜆
Se escribe:
𝑋 𝑃(𝜆) ,
si Su función de
probabilidad es:
𝜆 = 𝑛 ∗ 𝑝

12. a) Que no ocurra ningún accidente en un mes
b) Que como máximo ocurran 2 accidentes en un mes
c) Que ocurran 30 accidentes en un año
d) que ocurran 8 accidentes en un trimestre
En una empresa el
término medio de
accidentes es de 3
por mes. Calcular la
probabilidad de:
EJEMPLO

13. Dr. Jorge Alejandro Obando Bastidas
Jorge.obandob@campusucc.edu.co