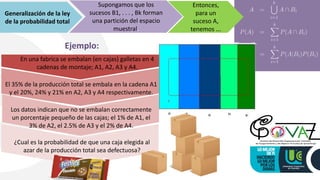
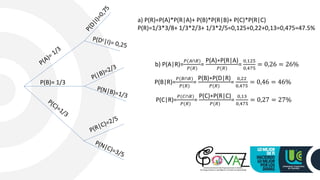
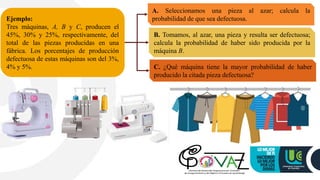
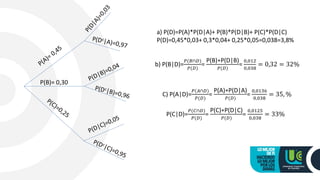
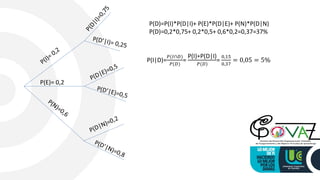
1) The document discusses probability and Bayes' theorem. It provides examples of calculating the probability of defective boxes being produced on different assembly lines and the probability a defective box came from a specific line. 2) It also gives examples of calculating the probability a randomly selected item is defective, and the probability a defective item came from a particular machine. 3) The final example calculates the probability that a randomly selected manager was an engineer, given data on the percentage of employees in different roles and the likelihood of having a management position.

1. “Probabilidad total y
teorema de Bayes”
Dr. Jorge Alejandro Obando Bastidas

2. Particiones
Se dicen que una serie
de sucesos, B1, . . . , Bk
forman una partición
del espacio muestral
si todos los
sucesos son
incompatibles
y luego Bi ∩ Bj = φ para
todo 1 ≤ i ≠j ≤ k y si
además, ∪𝑖=1
𝐾
Bi = Ω.
Una partición es una
división del espacio
muestra en distintos
bloques.

3. En una fabrica se embalan (en cajas) galletas en 4 cadenas de
montaje; A1, A2, A3 y A4.
El 35% de la producción total se embala en la cadena A1 y el
20%, 24% y 21% en A2, A3 y A4 respectivamente.
Los datos indican que no se embalan correctamente un
porcentaje pequeño de las cajas; el 1% de A1, el 3% de
A2, el 2.5% de A3 y el 2% de A4.
¿Cual es la probabilidad de que una caja elegida al azar
de la producción total sea defectuosa?
Supongamos que
descubrimos que una
caja es defectuosa.
Calculamos la
probabilidad de que
la caja provenga de la
cadena A1.

4. Generalización de la ley
de la probabilidad total
Supongamos que los
sucesos B1, . . . , Bk forman
una partición del espacio
muestral.
Entonces,
para un
suceso A,
tenemos ...
Ejemplo:
En una fabrica se embalan (en cajas) galletas en 4
cadenas de montaje; A1, A2, A3 y A4.
El 35% de la producción total se embala en la cadena A1
y el 20%, 24% y 21% en A2, A3 y A4 respectivamente.
Los datos indican que no se embalan correctamente
un porcentaje pequeño de las cajas; el 1% de A1, el
3% de A2, el 2.5% de A3 y el 2% de A4.
¿Cual es la probabilidad de que una caja elegida al
azar de la producción total sea defectuosa?

5. En una fabrica se embalan (en cajas) galletas en 4
cadenas de montaje; A1, A2, A3 y A4.
El 35% de la producción total se embala en la cadena A1
y el 20%, 24% y 21% en A2, A3 y A4 respectivamente.
Los datos indican que no se embalan correctamente
un porcentaje pequeño de las cajas; el 1% de A1, el
3% de A2, el 2.5% de A3 y el 2% de A4.
¿Cual es la probabilidad de que una caja elegida al
azar de la producción total sea defectuosa?
D= defectuosa
P(D)=P(A1)*P(D|A1)+ P(A2)*P(D|A2)+ P(A3)*P(D|A3)+ P(A4)*P(D|A4)
P(D)=0,35*0,01+ 0,2*0,03+ 0,24*0,025+ 0,21*0,02
P(D)=0,0197=1,97%
.
Calculamos la
probabilidad de
que la caja
provenga de la
cadena A1.
P(A3|D)=
𝑃(𝐴3∩𝐷)
𝑃(𝐷)
=
P(A3)∗P(D|A3)
𝑃(𝐷)
=30,4%
P(A2|D)=
𝑃(𝐴2∩𝐷)
𝑃(𝐷)
=
P(A2)∗P(D|A2)
𝑃(𝐷)
= 30,4%
P(A1|D)=
𝑃(𝐴1∩𝐷)
𝑃(𝐷)
=
P(A1)∗P(D|A1)
𝑃(𝐷)
=
0,0035
0,0197
= 0,177 =17,7%
P(A4|D)=
𝑃(𝐴4∩𝐷)
𝑃(𝐷)
=
P(A4)∗P(D|A4)
𝑃(𝐷)
=21,6%

6. Ejemplo:
Tres máquinas, A, B y C, producen el
45%, 30% y 25%, respectivamente, del
total de las piezas producidas en una
fábrica. Los porcentajes de producción
defectuosa de estas máquinas son del 3%,
4% y 5%.
A. Seleccionamos una pieza al azar; calcula la
probabilidad de que sea defectuosa.
B. Tomamos, al azar, una pieza y resulta ser defectuosa;
calcula la probabilidad de haber sido producida por la
máquina B.
C. ¿Qué máquina tiene la mayor probabilidad de haber
producido la citada pieza defectuosa?

7. P(B)= 0,30
a) P(D)=P(A)*P(D|A)+ P(B)*P(D|B)+ P(C)*P(D|C)
P(D)=0,45*0,03+ 0,3*0,04+ 0,25*0,05=0,038=3,8%
b) P(B|D)=
𝑃(𝐵∩𝐷)
𝑃(𝐷)
=
P(B)∗P(D|B)
𝑃(𝐷)
=
0,012
0,038
= 0,32 = 32%
C) P(A|D)=
𝑃(𝐴∩𝐷)
𝑃(𝐷)
=
P(A)∗P(D|A)
𝑃(𝐷)
=
0,0136
0,038
= 35, %
P(C|D)=
𝑃(𝐶∩𝐷)
𝑃(𝐷)
=
P(C)∗P(D|C)
𝑃(𝐷)
=
0,0125
0,038
= 33%

8. ¿Cuál es la probabilidad de haber sido una bola roja, extraída
de la urna A?
Tenemos tres urnas:
A con 3 bolas rojas y 5 negras.
B con 2 bolas rojas y 1 negra.
C con 2 bolas rojas y 3 negras.
Escogemos una urna al azar y extraemos una bola. Si la
bola ha sido roja.
A
B
C

9. P(B)= 1/3
a) P(R)=P(A)*P(R|A)+ P(B)*P(R|B)+ P(C)*P(R|C)
P(R)=1/3*3/8+ 1/3*2/3+ 1/3*2/5=0,125+0,22+0,13=0,475=47.5%
b) P(A|R)=
𝑃(𝐴∩𝑅)
𝑃(𝑅)
=
P(A)∗P(R|A)
𝑃(𝑅)
=
0,125
0,475
= 0,26 = 26%
P(B|R)=
𝑃(𝐵∩𝑅)
𝑃(𝑅)
=
P(B)∗P(D|R)
𝑃(𝑅)
=
0,22
0,475
= 0,46 = 46%
P(C|R)=
𝑃(𝐶∩𝑅)
𝑃(𝑅)
=
P(C)∗P(R|C)
𝑃(𝑅)
=
0,13
0,475
= 0,27 = 27%

10. El 20% de los empleados de una empresa son ingenieros y otro
20% son economistas. El 75% de los ingenieros ocupan un puesto
directivo y el 50% de los economistas también, mientras que los no
ingenieros y los no economistas solamente el 20% ocupa un puesto
directivo. ¿Cuál es la probabilidad de que un empleado directivo
elegido al azar sea ingeniero?
I= Ingenieros
E= Economista
N = No son ingenieros ni economistas

11. P(E)= 0,2
P(D)=P(I)*P(D|I)+ P(E)*P(D|E)+ P(N)*P(D|N)
P(D)=0,2*0,75+ 0,2*0,5+ 0,6*0,2=0,37=37%
P(I|D)=
𝑃(𝐼∩𝐷)
𝑃(𝐷)
=
P(I)∗P(D|I)
𝑃(𝐷)
=
0,15
0,37
= 0,05 = 5%

12. Dr. Jorge Alejandro Obando Bastidas
Jorge.obandob@campusucc.edu.co