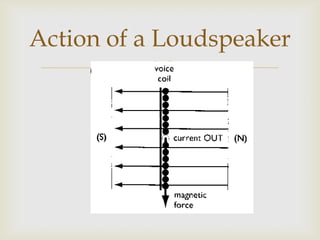
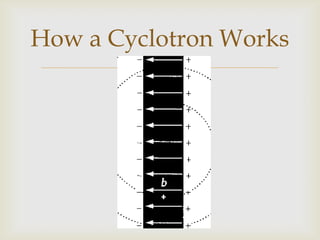
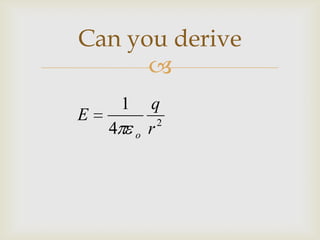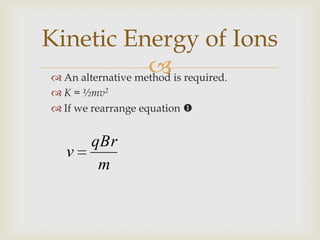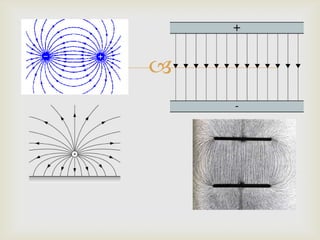
This document discusses electric fields, including Coulomb's law, electric field lines, and the motion of charged particles in electric fields. Some key points include: - Coulomb's law describes the electrostatic force between two point charges and is analogous to Newton's law of universal gravitation. - Electric field lines represent the strength and direction of an electric field graphically. They originate on positive charges and terminate on negative charges. - Charged particles experience a force when moving through an electric field, causing them to accelerate. Their motion can be analyzed using concepts from kinematics.

1. Electric FieldsSection 2Topic 1

2. All matter is made up of atoms and molecules;contain charged particles,the proton and electron.The charges on each are equal;but opposite in sign.Charges

3. Fq1 and F q2 Discovered a relationship between;force (F),distance (r) between the centres of the objects.Coulomb’s Law

4. Coulomb’s LawThe value of the constant is;9.00 x 109 Nm2C-2, in a vacuum.The constant is written as:o is the permittivity in a vacuum or the ability to transmit electric force.Force is a vector and so must have a direction.The force is along a line joining the two centres. If charges are the same,there is repulsionIf different,there is attraction.Coulomb’s Law states:Coulomb’s Law

5. The force acting between two charges q1 and q2;who are separated by a distance d,is directly proportional to the product of the charges,and inversely proportional to the square of the distance between them.The force is along the line joining the centres of the charges.Coulomb’s Law

6. This is similar to Newton’s law of universal gravitation:Coulomb’s Law

7. Coulomb’s & Newton’s Law1. The interaction acts on both bodies.2. Both forces act at a distance without the bodies touching.3. Both directly proportional to the product of the properties causing the interaction.4. Both inversely proportional to the distance between the bodies.5. Forces are consistent with N III

8. They are dissimilar in that:1. Gravitation is a force of attraction only while charges can attract and repel.2. The force between charges depends on the medium while gravity does not.Coulomb’s & Newton’s Law

9. As force is a vector we cannot algebraically add forces if there is more than one point charge present.The law that we use to determine to total force is called the law of superposition.When two or more point charges are present;the total force is equal to,the vector sum of the forces,due to each of the other point charges.Principle of Superposition

10. To use this principle, follow the rules given below:1. Draw a labelled diagramUse coulombs law to determine the magnitude;ignore the direction at this stage3. Determine if the force is attractive or repulsive.4. Repeat step 2 for any other combinations of charges.5. Draw a vector diagram.Principle of Superposition

11. Find the resultant;using Pythagoras theorem,trigonometryDetermine the direction using trigonometry.Principle of Superposition

12. An electric field is a region in space where;an object will experience a force due to,its charge,without the charges necessarily touching.The Electric Field

13. A diagram representing the relative strength of a field at any point can be drawn.The lines drawn give,direction of the force on a tiny positive charge.If the charge were allowed to move,the charge would move along the field line.Lines of Electric Force

14. Rules for drawing electric field line diagrams.1. Lines of electric force are always directed from positive to negative charges.Lines of Electric Force

15. Lines of electric force always start and end on a charged surface;make an angle of 90o to that surface.If the surface is curved;construct a line at 90o to the tangent at that point.Lines of Electric Force

16. 3. Lines of electric force never cross.There is no electric field inside a hollow conductor,hence no lines of electric force exist.Lines of electric force are found to concentrate;at regions of high curvature on a conductor.Lines of Electric Force

17. The field may be strong enoughat the sharp pointto ionise the air.Charges may then move awayfrom the conductor.This is called Corona Discharge.Lines of Electric Force

18. Make sure that the number of field lines per unit area represents the field strength;when close together the field is strong,when far apart the field is weak. Where the field lines are parallel and equally spaced;the field is said to be uniform.Lines of Electric Force

19. The field becomes curved;or non uniform.This is known as the end effect.If the separation of the plates becomes too large;the end effect encroaches on the region between the plates.Lines of Electric Force

21. The electric field strength, E,at a point in an electric field is given by the force, F,acting on a unit positive charge placed at that point in the field.Units for E are NC-1.It is a vector with both magnitude and direction.Electric Field Strength

22. Consider two charges;a fixed point charge q and a test charge qT,separated by a vacuum by a distance r.Coulomb’s law gives the force each feels;directions will be opposite (NIII).Derivation

23. Can you derive

24. If more than one charge exists in an electric field, the total field at any one point is;the vector sum of the electric field strengths due to each charge.Etotal = E1 + E2 + E3 + …….+ EnElectric Field Strength Due to Several Charges

25. Electric Field Strength Due to Several ChargesExample

26. Electric Field Strength Due to Several Charges

27. There are five steps in the process.The examination will focus only on corona dischargePhotocopiers & Laser Printers

28. Step 1:Charging the Photoconductive Drum.The drum has the special property of being an electrical insulator in the dark;an electrical conductor when exposed to light.Near the drum is a thin corona wire;voltage of about 6000V between it and the drum,extends for the length of the drum.The polarity can vary depending on the design.Photocopiers & Laser Printers

29. The material used to coat the earthed aluminium drum;3 - 15 cm in diameter,to achieve this effect is commonly selenium.Photocopiers & Laser Printers

30. The electric field near the corona wire;accelerates any ions in the atmosphere,to high velocities.They in turn collide with neutral atoms in the air;knocking out some electrons.These free electrons attach themselves to other neutral atoms.From this process;large amounts of positive and negative ions are formed,as more and more collisions occur.Photocopiers & Laser Printers

31. These charged ions are attracted to either;the corona wire,or the drum.On reaching the drum;they charge the photoconductive coating uniformly,as the drum rotates.Photocopiers & Laser Printers

32. Transferring the Toner to the PaperThe paper is charged the same sign as that on the drum;using another corona wire,called the transfer corona.Photocopiers & Laser Printers

33. So the paper does not cling to the drum, the extra charge on the paper is removed;using another oppositely charged corona wire,called the separation corona.Photocopiers & Laser Printers

34. Motion of Particles in Electric FieldsSection 2Topic 2

35. W = FsW = Uand U = qEd;this can be equated to a gravitational field,U = mgh.d = distance the charge q;is moved in a uniform field E.W = qEdV = EdW = qV Electric Potential Difference

36. The electric potential difference between two points in an electric field is;the work done W in moving a positive test charge moved between the points,provided that all other charges remain undisturbed.The unit for electric potential difference is;JC-1,which is also known as;volt (V).Electric Potential Difference

37. Change in potential = EdThis is called the potential difference,V.V = Ed;d = distance between two points;parallel to the field.More on P.D.A more common way of expressing this is:

38. If an electron is accelerated;across a potential difference of 5 volts,K.E. = 5 times its chargei.e. 5 x 1.6 x 10-19 = 8.0 x 10-19JOne electron volt is the energy that an electron would gain;if it were to accelerate,across a potential difference of 1 volt.Symbol for the electron volt is eV.1 electron volt = 1.6 x 10-19 JElectron Volt

39. A charge that is free to move in a uniform electric field;behaves in a similar way to a mass in a gravitational field.In a gravitational field, an object which moves towards the earth;experiences a force that converts P.E. to K.E.When energy is converted from one form to another;work is done.No work is done in the component that is parallel to the ground.Motion of Charges in a Field

40. In an electric field, the same applies.When a charge moves parallel to the conducting surface;no work is done.The force only acts radially from the surface;its velocity is unchanged.There cannot be a field inside a conductor no matter its shape.Motion of Charges in a Field

41. A charged particle that is free to move in a uniform electric field;behaves in a similar way to a,particle in a gravitational field.Acceleration can be found by modifying Newton II.While a charge remains in the electric field;it will continue to accelerate uniformly.Motion of Charged Particles in a Uniform Electric Field

42. Note:These equations only apply in a uniform field where;the acceleration is constant. The motion in two dimensions;must use vector techniques.Two other points must also be remembered:Motion of Charged Particles in a Uniform Electric Field

43. The acceleration of a particle is either;parallel to the lines of force;(+ive charge)or antiparallel (-ive charge).Any motion at an angle to the lines of electric force;will result in a parabolic path.The motion can be divided into its components;which are independent of each other. Motion of Charged Particles in a Uniform Electric Field

44. Motion of Charged Particles in a Uniform Electric FieldParallel component will undergo acceleration;perpendicular component will not.http://www.physics.sjsu.edu/becker/physics51/e_and_v.htm

45. Magnetic FieldsSection 2 Topic 3

46. Magnetic fields are produced by moving electric charges;hence by electric currents.In a bar magnet;iron atoms have electrons that spin.Each spinning electron;tiny ‘magnet’.Magnetic Fields

47. As all the electrons spin in the same direction;there is no cancellation,magnetic field is stable.Field lines can represent magnetic fields;As they did in electric fields.Magnetic Fields

48. Magnetic Fields

49. The field is concentric circles centred on the wire;strongest near the wire.This magnetic field is in addition to;electric field produced by the charges.Oersted’s Law

50. To determine the direction of the magnetic field around a wire;use Oersted’s right hand rule.Oersted’s Law

51. Grab the wire with your right hand,Thumb in the direction of the conventional current, I;(i.e. +ive to -ive),Field is in the direction of;curl of your fingers.Oersted's LawOersted’s Law

52. To increase the strength of the field increasing the current;the wire can be bent into a loop.Current flow through a circular coilOersted’s Law

53. To further increase the strength of the field at the centre of the loop;several loops are used instead of the single wire,to form a flat coil.Each loop of current carrying wire contributes;to a stronger magnetic field.Oersted’s Law

54. Oersted’s LawCurrent flow through a solenoid

55. Magnetic Force Around a Current-Carrying Conductor

56. Magnetic Force Around a Current-Carrying Conductor

57. F = BIlsinθF is the force on the wire,in newtons,I is the current flowing in the wire,in amperes,B is the magnetic induction of the magnetic field,in tesla,lsinθis the length of wire in the magnetic field,in metres.Magnetic Force Around a Current-Carrying Conductor

58. F = BIlsin is the angle;between the wire,and the magnetic field.Note sin is at a maximum when; = 90o,ie when Band I are perpendicular.Magnetic Force Around a Current-Carrying Conductor

59. This leads to the definition of BThe magnitude B of a magnetic field is defined as the force per current element placed at right angles to the field.The direction of magnetic induction is perpendicular to both the force and the current element.Magnetic Force Around a Current-Carrying Conductor

60. The principle of a moving coil loudspeaker is that;a coil carrying an electric current,oscillating with amplitude,and frequency,proportional to the sound to be produced,is suspended in a uniform magnetic field.Moving Coil Loudspeaker

61. ComponentsCross section of a Speaker

62. Action of a Loudspeaker

63. Action of a Loudspeaker

64. Motion of Particles in Magnetic FieldsSection 2Topic 4

65. Charges that are stationary;have no magnetic force applied to it.A wire that has no P.D. applied to its ends;has no magnetic force associated.We have investigated current carrying conductors;and the magnetic force associated with it.Forces on Moving Charges

66. Another way to produce an electric current is;to have a moving beam of charged particles.If the beam were to move perpendicularly into a magnetic field;then every charged particle would experience a force.Forces on Moving Charges

67. It must be perpendicular as from;F = BIl sin , sin  = 0.Force would be zero;if the motion was parallel to the field.If the beam was visible;seen to be deflected by,magnetic interaction.Forces on Moving Charges

68. The magnitude of the force acting on the beam is determined by:F = BIlIl needs to be determined for a beam of particles; each of charge q,moving at a constant speed v.The force on the beam is F=IlB=nqvBThus the force on each particle = qvBForces on Moving Charges

69. Substituting into F = BIlsin;F = qvB sinWhere  is the angle between v and B.This equation gives the magnitude;direction is determined by the right hand palm rule.Forces on Moving Charges

70. A beam of charged particles in a magnetic field;can follow a semi-circular path,with uniform circular motion.The radius and other features can easily be determined.The magnetic force,supplies a centripetal force, therefore:Forces on Moving Charges

71. Forces on Moving ChargesFB = Fcand rearranging gives the equation:

72. This deflection occurs because;the charged particles are no longer constrained by,the lattice of metal ions in the wire. The deflection of the beam is determined;by the right hand palm rule.Be careful as the thumb must point in the direction of conventional current;i.e. +ive to -ive.Forces on Moving Charges

73. The period of the motion and the frequency of revolution can be deduced from:Forces on Moving Charges

74. A cyclotron is a device used;to accelerate charged particles to high energies,generally so they may collide with atomic nuclei,and produce a nuclear reaction.Applications – Cyclotrons

75. Applications – Cyclotrons

76. There are three main parts of a cyclotron:1. Ion SourceA beam of protons;or sometimes deuteron,which is heavy hydrogen. Can be charged particlePositive IonNegative IonApplications – Cyclotrons

77. Modern ion sources are generated from an electric arc;external to the cyclotron,vacuum is not compromised.Applications – Cyclotrons

78. Applications – Cyclotrons

79. 2. Semicircular Metal Containers (‘dees’)Originally, two hollow copper electrodes;shaped like the letter ‘D’,their straight edges facing each other were used.Applications –Cyclotrons

80. A large ac P.D. is applied between the dees.The P.D. creates an electric field;in the gap between them,that is continuously changing.As the dees are closed hollow metal conductors;they have no electric field inside of them.Applications –Cyclotrons

81. The dees are in a magnetic field;produced by an electromagnet.This means that there is a magnetic field;within the dees.Within the gap there exists;an electric and magnetic field.Applications –Cyclotrons

82. 3. Evacuated Outer ChamberThe dees are placed;within an outer evacuated container.Applications –Cyclotrons

83. The function of the electric field;accelerate the ions to high energies.The longer the ions is in the electric field;the higher the energy.How a Cyclotron Works

84. The function of the magnetic field;Make the ions move in a circular path;it repeatedly comes under the influence of the electric field,increases the energy level.How a Cyclotron Works

85. How a Cyclotron Works

86. How a Cyclotron Works

87. How a Cyclotron Works

88. How a Cyclotron WorksCyclotron

89. As the ions pass through the gap;their speed increases,so must their kinetic energy.This means work is done.From previously;W = qVAs there are two passes of the gap per revolution;their kinetic energy per revolution,is 2qV.Energy Transferred to the Ions

90. The dees are placed between;poles of an electromagnet.The ions are not shielded from;magnetic field,unlike the electric field.This means the ions are affected;inside thedees,in the gap between them.Application- Cyclotrons

91. To make the ions move in circular path;uniform magnetic field is needed,perpendicular to the plane of the dees.Polarity of the field is important;to make the ions move in the right direction.The force is such that;always acting towards the centre of the circle,causing centripetal acceleration.Application- Cyclotrons

92. Application- CyclotronsThe field must be in a direction which is;

93. OUT of the page.Period of Circular MotionAnd F = qvBtherefore, upon rearrangement:

94. As the mass m;charge q,magnetic field B,are all constant,rvPeriod of Circular Motion

95. We also stated:The time for the ion to complete one semicircle is the same irrespective of the speed of the ion.From before, if the speed doubles;radius doubles.Period of Circular Motion

96. This also doubles the;circumference (2r).Mathematically, this can also be shown to be true.The velocity of an object undergoing circular motion is given by:Period of Circular Motion

97. Period of Circular MotionRearranging for TFrom  we can substitute for r.

98. This shows that the period is;independent of speed,or radius.Period of Circular Motion

99. An alternative method is required.K = ½mv2If we rearrange equation Kinetic Energy of Ions

100. Substituting into formula for K:Kinetic Energy of Ions

101. This indicates that the kinetic energy of an ion;of given charge,and mass.Only depends on the radius;of the final circle,magnitude of the magnetic field.This can be understood due to two points.Kinetic Energy of Ions

102. Point 1If the magnetic field increases;the radii decreases,ions make more revolutions,more crossings of the gap between the dees.Kinetic Energy of Ions

103. At each crossing;they are accelerated,to higher kinetic energy.Increasing the magnetic field results in;increase of the kinetic energy,of the emerging ions,at a given radius.Kinetic Energy of Ions

104. Point 2If the P.D. is increased;the ions gain more speed with each crossing of the gap,and so make circles with larger radii,and make fewer revolutions.This means that a larger P.D. does not result in;a larger kinetic energy,of the emerging ions at a given radius.Kinetic Energy of Ions

105. The protons are used to bombard stable atoms;carbon,nitrogen,oxygen,Fluorine.To produce radioactive forms of these elements.Uses of Cyclotrons in Hospitals

106. They are then combine with glucose and are given to the patient.The radioactivity can then be detected;bodily functions that use the above chemicals,can be monitored.A medical diagnosis can then be made.Uses of Cyclotrons in Hospitals