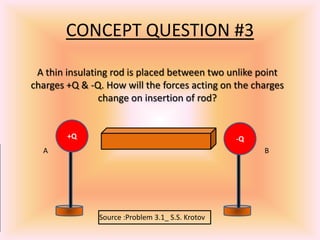
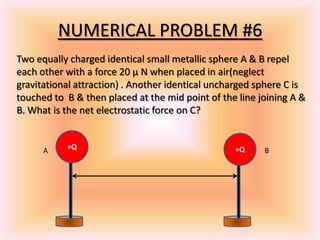
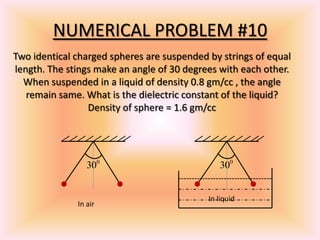
This document presents a PowerPoint presentation on electrostatics and Coulomb's law. It discusses how Coulomb experimentally determined that the electric force between two charges is directly proportional to the product of the charges and inversely proportional to the distance between them. It also provides Coulomb's law equations in scalar and vector forms. Several examples of applying Coulomb's law to calculate electrostatic forces are presented. The document concludes by discussing the principle of superposition for Coulomb's forces and providing additional practice problems for determining electrostatic forces.

1. ELECTROSTATICS-PART 2
A POWERPOINT PRESENTATION
BY
BRAJESH KUMAR CHAUDHARY
FACULTY OF PHYSICS
RESONANCE EDUVENTURES PVT. LTD.
NAGPUR, INDIA.

2. COULOMB’S LAW
CHARLES COULOMB
(1736-1806)
The electric force between two charges is
• proportional to the product of the
charges ,and
•inversely proportional to the distance
between them.

3. COULOMB’S LAW
Coulomb used a torsion balance to investigate
electrostatic forces. A quantity of charge Q is
rubbed on a fixed sphere B. A second charge
q is rubbed on a sphere A on the end of a
suspended rod that is free to rotate. The force
exerted by Q on q twists the rod and
suspending fiber. Turning the suspension head
twists the fiber back so that the two spheres
stay the same distance apart. The magnitude of
the force is indicated by the angle through
which the suspension head is turned. Coulomb
found that the force exerted by one charge on
another was directly proportional to the
magnitudes of both charges (Q.q). He also
found that force was inversely proportional to
the square of the distance, r, between the
charged spheres.

4. COULOMB’S LAW(Contd.)
Force between the two particles in
a medium
1 2
21 12 2
q q
F F K
r
Where,
=force on particle 2 due to 1
=force on particle 1 due to 1
= distance between 1 & 2
K = a constant of the medium
21F
12F
r

5. COULOMB’S LAW(Contd.)
In vector form,
1 2
21 2
ˆ
q q
F K r
r

1q
2q
r
ˆr
Where
= unit vector in the increasing direction of rˆr

6. COULOMB’S LAW(Contd.)
•Valid for point charges only
• , where is permittivity of medium
• = =permittivity of free space
= relative permittivity of medium also known as
dielectric constant of the medium
= 1 for free space
= for conductors
1
4
K
0 r
0
r
r
r
9 2 2
9 10 Nm C

7. COULOMB’S LAW(Contd.)
•It is a conservative force.
•It is a central force i.e., the force between the two particles is
always along the line joining the two particles.
•Since it is central, hence in the absence of any external force,
angular momentum of one particle with respect to the other (in
two particle system) is conserved.

8. PRINCIPLE OF SUPERPOSITION FOR
COULOMB’S FORCE
Electrostatic force is a two body interaction i.e. electrical force between two
point charges is independent of presence or absence of other charges & so the
principle of superposition is valid.
THUS,
Force on charged particles due to number of point charges is the resultant of
forces due to individual point charges. Therefore, force on a point test charge
due to many charges is given by
1 2 3 ...F F F F
    Q 1F

2F

3F


9. CONCEPT QUESTION #3
+Q
A
-Q
B
A thin insulating rod is placed between two unlike point
charges +Q & -Q. How will the forces acting on the charges
change on insertion of rod?
Source :Problem 3.1_ S.S. Krotov

10. NUMERICAL PROBLEM#2
NaCl molecule is bound due to
electrical force between the
sodium & the chlorine ions
when one electron of sodium
is transferred to chlorine.
Taking the separation between
the ions to be ,
Find the force of attraction
between them. State the
assumptions (if any ) that you
have made.
8
2.75 10 cm
Source: Problem 13, Ch. 28_HCV

11. NUMERICAL PROBLEM #3
A hydrogen atom consists of one
proton & one electron. It may be
assumed that electron revolves in a
circle of radius 0.53 angstrom. With
the proton at its centre. The
hydrogen atom is said to be in ground
state in this case.
Find
(a)Magnitude of electric force
between the proton & the
electron.
(b)Find the speed of the electron in
this case.
Source: Problem 18,19, Ch. 28_HCV

12. NUMERICAL PROBLEM #3
Two charged particles having charges 20 nC each are
connected by an insulating string of length 1m & the
system is kept in a smooth horizontal table. Find the
tension in the string.
q
q
Source: Problem 21, Ch. 28_HCV

13. NUMERICAL PROBLEM #4
Five point charges , each of
value q are placed on five
vertices of a regular hexagon of
side L. What is the magnitude of
the force on a point charge of
value –q placed at the centre of
the hexagon?
L
q q
q
q
q
-q

14. NUMERICAL PROBLEM #5
+q
+q+q
-2q
Three equal point charges of
charge +q each are moving
along a circle of radius R and a
point charge -2q is also placed
at the centre of the circle as
shown in the gig. If the charges
are revolving with constant and
same speed, then calculate
speed of charges.

15. NUMERICAL PROBLEM #6
+Q +Q
Two equally charged identical small metallic sphere A & B repel
each other with a force 20 μ N when placed in air(neglect
gravitational attraction) . Another identical uncharged sphere C is
touched to B & then placed at the mid point of the line joining A &
B. What is the net electrostatic force on C?
A B

16. NUMERICAL PROBLEM #7
Source:Problem 3.3_I.E Irodov
Two small equally charged sphere, each of mass m, are
suspended from the same point by silk threads of length l.
The distance between the spheres x<<l. find the rate dq/dt
with which the charge leaks off each sphere if their
approach velocity varies as v= a/ √x , where a is a constant.

17. NUMERICAL PROBLEM #8
A thin wire ring of radius r has an electric charge
Q. What will be the increment in the force
stretching the wire if a point charge q is placed at
the centre.
q
Q
Source:Problem 3.5_I.E Irodov

18. NUMERICAL PROBLEM #9
Given a cube of side a with point charges q on each of
its vertices. Calculate the force exerted on any of the
charges due to rest of the 7 charges.
q
qq
q
q
q q

19. NUMERICAL PROBLEM #10
Two identical charged spheres are suspended by strings of equal
length. The stings make an angle of 30 degrees with each other.
When suspended in a liquid of density 0.8 gm/cc , the angle
remain same. What is the dielectric constant of the liquid?
Density of sphere = 1.6 gm/cc
0
30 0
30
In air
In liquid