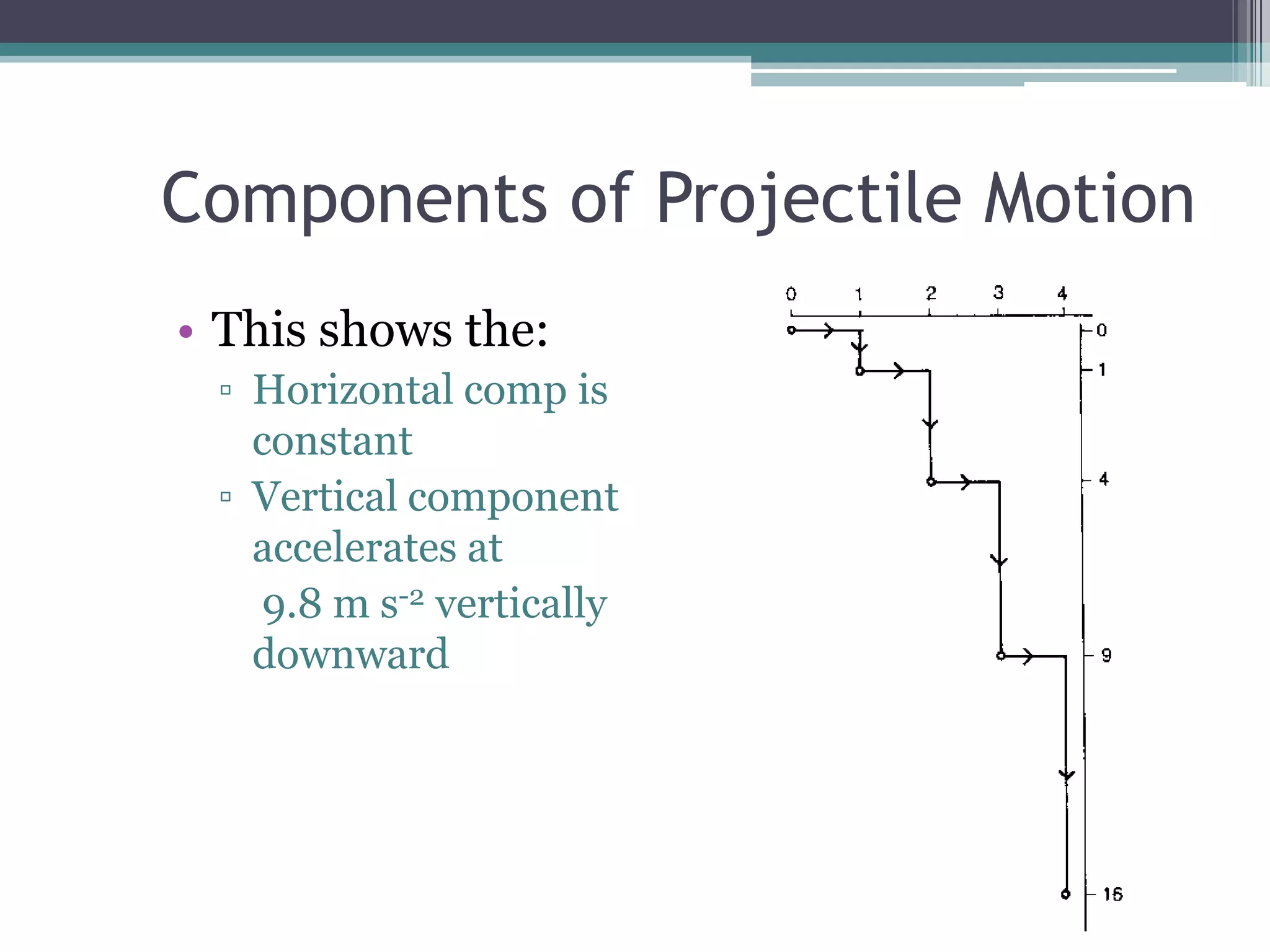
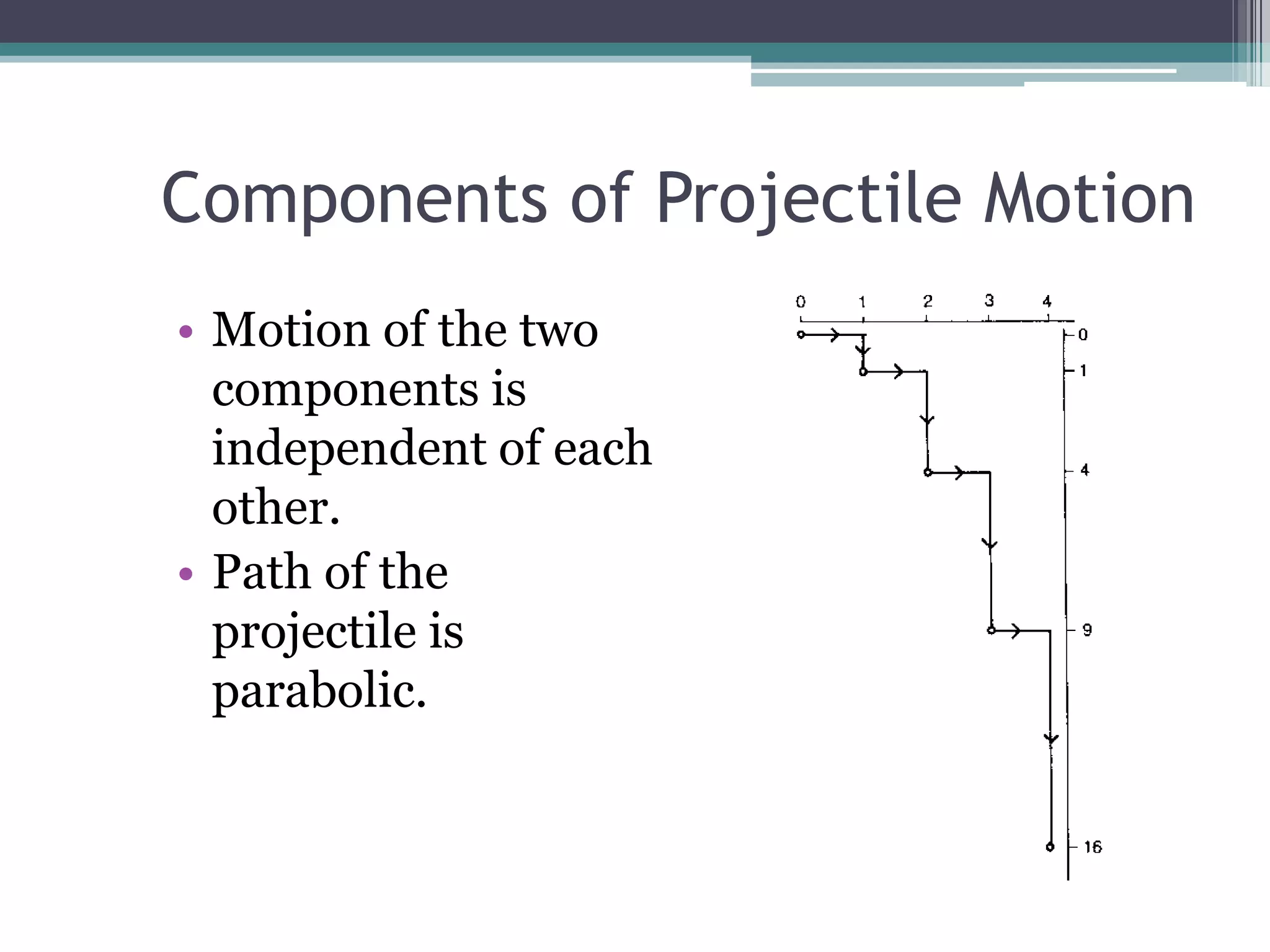
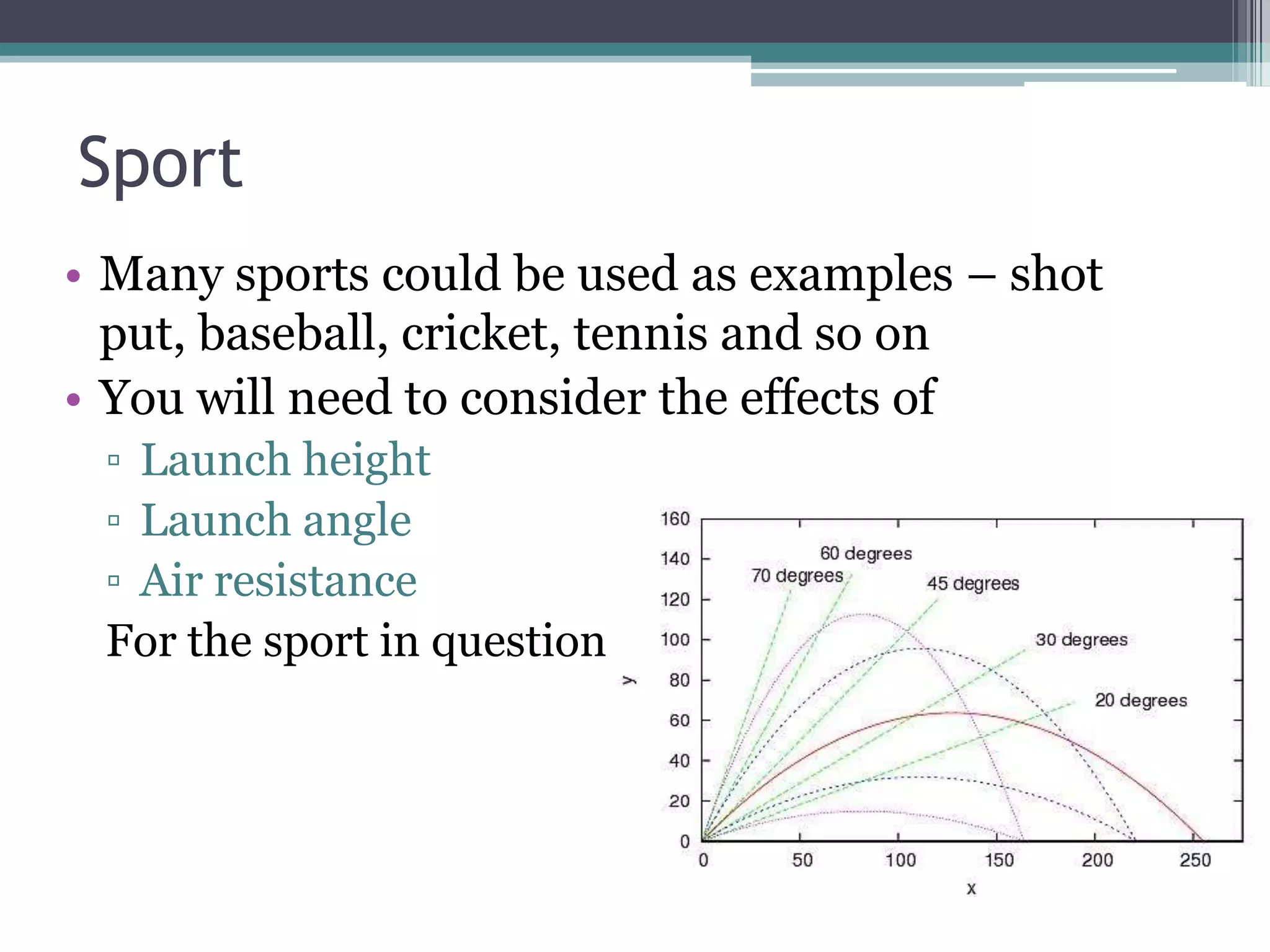
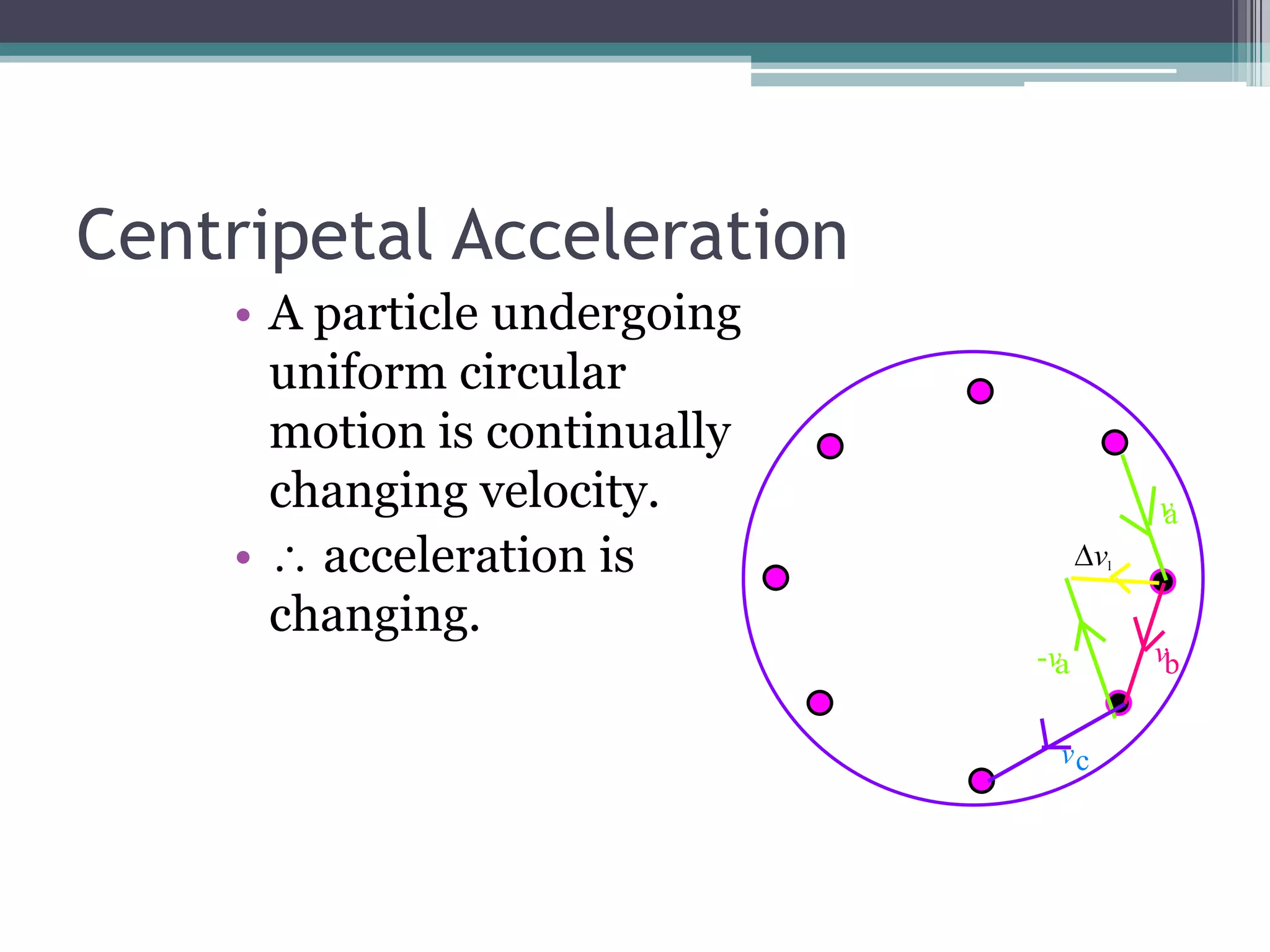
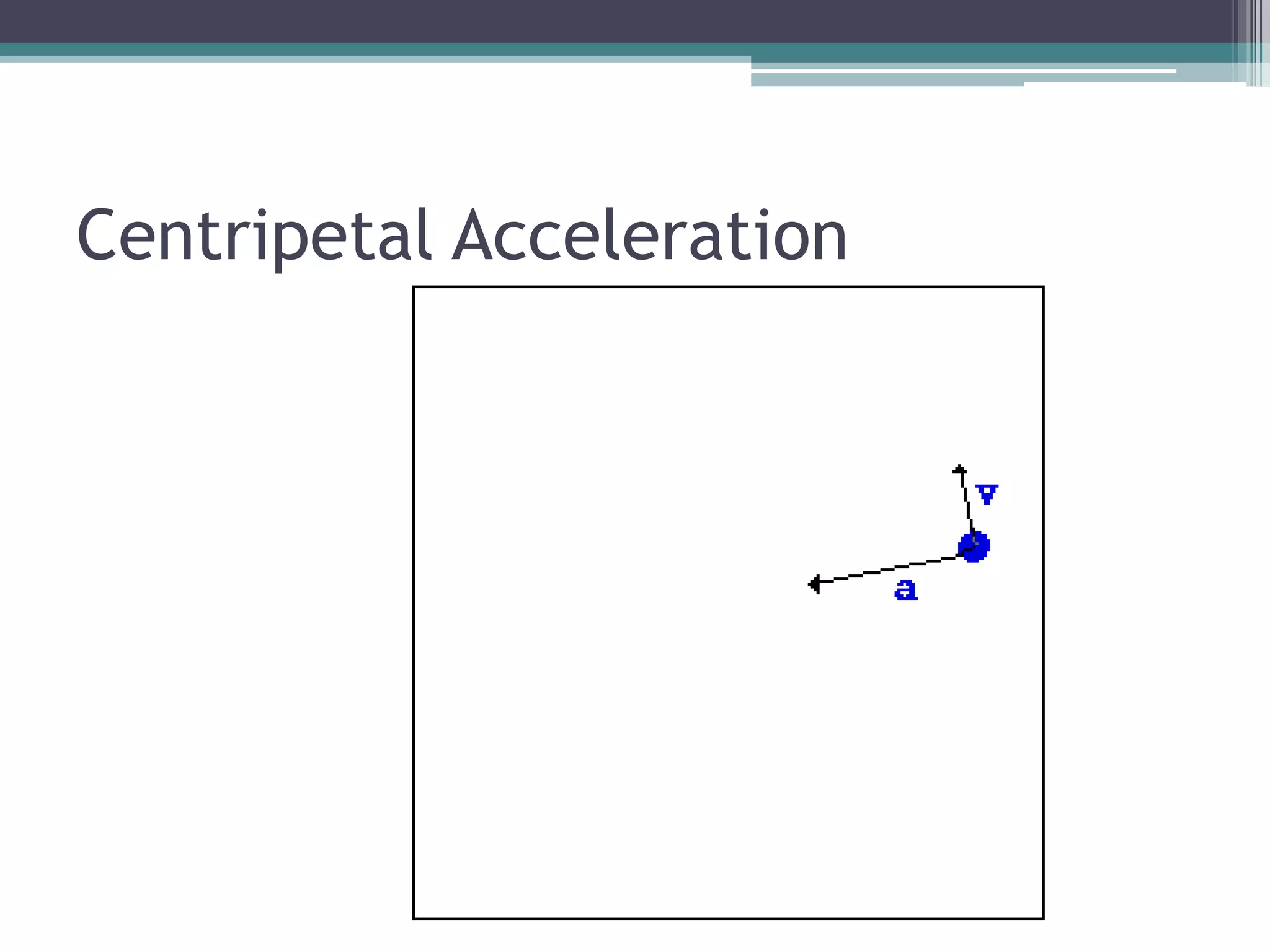
1) Projectile motion involves motion in two dimensions - horizontal and vertical. The horizontal motion is constant while the vertical motion accelerates downward at 9.8 m/s^2. 2) Uniform circular motion requires a centripetal force directed toward the center of rotation to cause centripetal acceleration. 3) Newton's law of universal gravitation describes the gravitational attraction between two objects, proportional to their masses and inversely proportional to the square of the distance between them.

1. Projectile MotionSection 1: Topic 1

2. VectorsThe length of the line represents:the magnitude and,The direction of the line segment represents:the direction of the vector quantity.

3. Kinematic Equationsvf = vo + at(no s)vf2 – vo2 = 2as(no t)s = vot + ½ at2 (no vf)s = vtt – ½ at2 (no vo) (no a)

4. Components of Projectile MotionThe motion is in two dimensionsHorizontal (perpendicular to the gravitational field)Vertical(parallel to thegravitational field)

5. Components of Projectile Motion

6. Components of Projectile MotionThis shows the:Horizontal comp is constantVertical component accelerates at 9.8ms-2 vertically downward

7. Components of Projectile MotionMotion of the two components is independent of each other.Path of the projectile is parabolic.

8. Labelling the diagramaaaaaaKey here is to check what labels you’ve been asked to add – velocity? force? acceleration?

9. Aiming a banana above a monkey’s head

10. Aiming a banana above a monkeys head and he lets go of the branch

11. Components of Projectile MotionBoth the banana and the monkey accelerate at the same rate downwards.Both fall the same amount below their gravity free path.Banana passes over the monkey’s head.Passes over by the same amount as it was originally aimed over the monkey’s head.

12. Components of Projectile MotionWhat happens if you aim at the monkey?

13. Components of Projectile MotionWhat happens if the banana is fired slowly?

14. Determining Characteristics of ProjectilesStep 1Determining Initial Components

15. Determining Characteristics of ProjectilesHorizontal ComponentviH = vicosVertical ComponentviV = visin

16. Determining Characteristics of ProjectilesStep 2Determining Time to Maximum HeightNote: Only vertical component affects the height.

17. Determining Characteristics of Projectilesvfv = vov + ata = -9.8ms-2 (i.e. acceleration is in the opposite direction to the motion when the projectile is still climbing) 0 = voV + atvv = 0 (at maximum height)

18. Determining Characteristics of ProjectilesStep 3Determining Maximum HeightNote: Only vertical component affects the heightsv = voVt + ½at2a = -9.8ms-2 (i.e. acceleration is in the opposite direction to the motion)Use t from Step 2

19. Determining Characteristics of ProjectilesStep 4Determining rangeNote: Only horizontal component affects range. If the ground is flat, the time in the air = 2 x time to maximum heightsh = voHt + ½ at2a = 0 in horizontal componentsh = voHtt = 2 x value of t in Step 2

20. Determining Characteristics of ProjectilesStep 5

21. Determining Position at Any Time

22. Horizontal component:sh = viHtThis gives distance down the range

23. Determining Characteristics of ProjectilesVertical component: sv = vtVt + ½ at2a = -9.8 ms-2This gives distance above ground. (i.e. acceleration is in the opposite direction to the motion)

24. Firing Projectiles HorizontallyWhat happens when you fire a projectile that has only a horizontal component?

25. Dropping VerticallyWhat happens if you drop a parcel from a plane?

26. Firing Vertically UpwardsWhat happens if you fire an object vertically upwards from a moving vehicle?

27. Firing Projectiles Non - Horizontally

28. Maximum RangeWhat angle gives you the maximum range?

29. Different Launch Height The final height may be different from the initial height.How does this change the characteristics of flight? The object will still follow a parabolic path.It will travel further.It will drop further vertically with each unit of time than if launched at the same height.

30. Different Launch HeightIf you are throwing a ball from shoulder height which is going to land on the ground:

31. 45o is no longer the best launch angle.

32. A shallower angle is better.Effect of Air ResistanceMost projectiles do not follow a perfect parabolic path as there is another force besides gravity that acts on the projectile.This force is due to the medium it travels through. In most cases, this is air.

33. Effect of Air ResistanceAir is a retarding force and so resists the motion.Retardation depends on the size, shape and mass, speed, texture of the object.It also depends on the density of the airA large surface area will result in greater air resistance effects.A streamlined ‘bullet’ shape will minimise the effect of air resistance.

34. SportMany sports could be used as examples – shot put, baseball, cricket, tennis and so on

35. You will need to consider the effects of

36. Launch height

37. Launch angle

38. Air resistanceFor the sport in question

39. Uniform Circular MotionSection 1 Topic 2

40. Circular MotionAn object moving in a circular path will have a constant speed.It is continually changing direction.Therefore it’s velocity is continually changing.A relationship can be determined for the speed of the object.

41. Circular Motion TermsPeriodIs the time needed to complete one cycle/rev (in secs). The symbol T is used.FrequencyNumber of cycles/revs completed per unit time.Units are Hertz (Hz)f =

42. Circular Motion TermsIn uniform circular motion, the object in one revolution moves 2r in T seconds.

43. Centripetal AccelerationA particle undergoing uniform circular motion is continually changing velocity. acceleration is changing.

44. Centripetal Accelerationv1 = vb - va.v2 = vc - vb and so on.The magnitude of v1 = v2.The direction is always to the centre of the circle.

45. Centripetal Acceleration

46. Force Causing the Centripetal AccelerationAny particle undergoing uniform circular motion is acted upon by an unbalanced force which is….Constant in magnitude.Directed towards the centre of the circle.Causes the Centripetal Acceleration.

47. Force Causing the Centripetal AccelerationMoon revolving around the Earth:Gravitational Force,Directed towards the centre of the Earth,Holds the moon in a near circular orbit.

48. Force Causing the Centripetal AccelerationElectrons revolve around the nucleus:Electric Force,Directed to centre of the nucleus,Holds electrons in circular orbit.

49. Force Causing the Centripetal AccelerationCar rounding a corner:Sideways frictional force,Directed towards centre of turn,Force between car tyre and road.If force not great enough:Car skids.

50. Centripetal Acceleration and FrictionThe force acts on the passenger in the car if they do not have their seat belt on.Note: it is an European car.

51. Force Causing the Centripetal AccelerationBilly can being swung.Vertically or horizontallyThe tension force between arm and cancauses the can to move in circular motion.

52. Centripetal Acceleration and the Normal ForceCar turns on a banked section of curved road: the chances of skidding is reduced.

53. Centripetal Acceleration and the Normal Force

54. Centripetal Acceleration and the Normal ForceIn the vertical direction, there are 2 forces; FNcos acting upwards and mg acting downwards. As there is no net vertical motion:FNcos = mg Centripetal Acceleration and the Normal ForceFor any radius curve and ideal speed, theperfect banking angle can be found.

55. Gravitation & SatellitesSection 1: Topic 3Section 1: Topic 3

56. Newton’s Law of GravitationNewton determined that a 1/d2.d = distance from the centres of the objects and not the surfaces.This is true for spherical objects.Newton’s 2nd law also states that Fa.This means that F  1/d2.

57. Newton’s Law of GravitationHis second law also says F m.As two masses are involved, Newton suggested that the force should be proportional to both masses.This is also consistent with his third law. If one mass applies force on a second object, the second mass should also apply an equal but opposite force on the first.

58. Newton’s Law of GravitationCombining these properties, we arrive at Newton’s law of universal gravitation. Turning this into an equality:Newton’s Law of GravitationDefinition:Between any two objects there is a gravitational attraction F that is proportional to the mass m of each object and inversely proportional to the square of the distance d between their centres.

59. Newton’s Law of GravitationWe can find the value of g at any height above the earth’s surface.

60. Satellites in Circular OrbitsObjectswill continue to move at a constant velocity unless acted upon by an unbalanced force.Newton’s first law.As satellites move in a circular path, their direction (and hence velocity) is continually changing.

61. Satellites in Circular OrbitsAs it is a circular orbit,

62. Satellites in Circular OrbitsThis will give the orbital velocity for a satellite to remain in an orbit of r from the centre of the Earth (ie re + r) irrespective of the mass of the satellite.Can you derive this equation?

63. Satellites in Circular OrbitsSpeed is also given by the equation:In one revolution,Orbiting satellite moves a distance equivalent to the circumference of the circular path it is following. 2r The time it takes for this revolution: Period (T). Hence;

64. Artificial Earth SatellitesSome orbits that are preferred over others.Meteorological and communication purposes. Polar orbit is useful as well.

65. Geostationary OrbitsThey must satisfy the following conditions:They must be equatorial.Only orbit in which the satellite moves in plane perpendicular to earth’s axis of rotation.The orbit must be circular.Must have a constant speed to match the earth’s rotation.

66. Geostationary Orbits The radius must match a period of 23 hrs 56 min.The radius, speed and centripetal acceleration can be calculated from the period.  The direction of orbit must be the same as the earth’s rotation.west to east.

67. Low Altitude Satellites200 - 3000 km above earth’s surface.Used for meteorology and surveillance.Smaller radius means smaller period.

68. Low Altitude SatellitesThe orbit is chosen so that:It passes over the same location twice each day at 12 hour intervals.6am and 6pm.Once in each direction.As seen from the ground.

69. Momentum in 2DSection 1: Topic 4

70. Newton’s Second LawIn vector form: F = maIndicates a relationship between force and acceleration.The acceleration is in the same direction as the net force.Implies the force on an object determines the change in velocity (aF)and

71. MomentumIs a property of a body that is moving.Vector quantity.If no net force is acting on the body/bodies, momentum is defined as the product of mass and velocity.

72. Momentump = mvUnits are given as kgms-1 or sN.Direction is the same as the velocity of the object.

73. Application of Newton IIDuring collisions, objects are deformed.

74. F = ma

75. For constant accelerationApplication of Newton IIFt = mvf - mvi Ft = p Ft= impulse of the force.Impulse causes the momentum to change. An impulse is a short duration force.Usually of non constant magnitude.

76. Application of Newton IIUnits are the same as those for momentumKgms-1 or sN.Defined as the product of the force and the time over which the force acts.During collisions, t is often very small.Fav is often very large.

77. Conservation of MomentumThe total momentum of all particles in an isolated system remains constant despite internal interactions between the particles.

78. Lets work through this

79. EnergyThe total energy in an isolated system is conserved.Energy can be transferred from one object to another.Energy can be converted from one form to another.The units are Joules (J).Is a scalar quantity.Does not have a direction. In collisions, total energy is always conserved.

80. EnergyThe kinetic energy will not always remain constant.May be converted to other forms. Could be:Rotational kinetic energySoundHeat.

81. Types of CollisionsElastic collisionsInelastic collisions.Momentum is conserved.No kinetic energy is lost.Occurs on the microscopic scale.Between nuclei.Momentum is conserved.Kinetic energy is lost.All macroscopic collisions are inelastic.Some collisions are almost elastic.Billiard balls.Air track/table gliders.

82. Flash Photography1. Distance between successive images is a measure of speed.2.Direction determined from multiple-imagephotograph.3. Line joining two successive images representmagnitude and direction of velocity vector.

83. Flash PhotographyTo calculate distance - measure distance between successive images and adjust by the scale.To calculate time - time between flashes =

84. Flash PhotographyMomentum:- Use velocity vector and let m1 = 1 unit and m2 is scaled accordingly.- This doesn’t change the validity of the process, only the scale for the momentum vector.7. Use vector diagrams for addition.

85. Spacecraft Propulsion

86. Spacecraft PropulsionAll vehicles move forward by pushing back on its surroundings.They obey Newton’s Third Law:For every action, there is a reaction.

87. Spacecraft PropulsionBefore a rocket is launched, it is stationary.No momentum.Total momentum after the rocket is fired:must also be zero.

88. Spacecraft PropulsionAfter the rocket is firedGases are ejected at high speed and, As the gas has mass, There is momentum acting in a direction directly opposite that in which the rocket is intended to move.To conserve momentum, there must be an equal momentum acting in the direction in which the rocket moves.

89. Spacecraft PropulsionMass of the rocket is large compared to the gas ejected, the velocity must be…..much lower.As gas is ejected, mass of the rocket….becomes less.and the velocity….becomes greater.

90. Spacecraft Propulsion

91. Spacecraft PropulsionIon ThrustersGeostationary SatellitesUsed for station keeping since 1980sLEOSuch as Iridium mobile communications clusterDeep space position controlCan fire ions in opposite direction to motion

92. Spacecraft PropulsionIon propulsion is a technique which involvesIonising gas rather than using chemical propulsionGas such as XenonHeavy to provide more momentumIs ionised and accelerated

93. Spacecraft PropulsionSolar SailsConverts light energy from the sun intoSource of propulsion for spacecraftGiant mirror that reflects sunlight toTransfer momentum from photons to spacecraft

94. Spacecraft PropulsionSolar Sails have lightAs propellantSunAs engineForce of sunlight at the EarthIs approx 4.70 N m-2

95. Spacecraft PropulsionPhotons bounce off (or absorbed) by sailDuring collisionmomentum conservedSmall mass provides small velocity change

96. Spacecraft PropulsionHowever, over timeLarge number of photonsContinuous forceLarge net forceeventuallyCannot be used to launch spacecraftStill need chemical rocket

97. Spacecraft PropulsionReflected photons cause greater accelerationthan absorbed photonsConsiderfor a given massp = mvAs velocity can change direction by 180ov can doublep can double

98. Spacecraft PropulsionIf photon is absorbedMomentum of spacecraftpis =pip =Final momentum of system

99. Spacecraft PropulsionIf photon reflectedInitial momentum of spacecraftps = pfp =As momentum must be conserved,p of systempsys =pfs =

100. Spacecraft PropulsionAs a = v/tFor reflected photonv can doublet is constantTherefore a can double