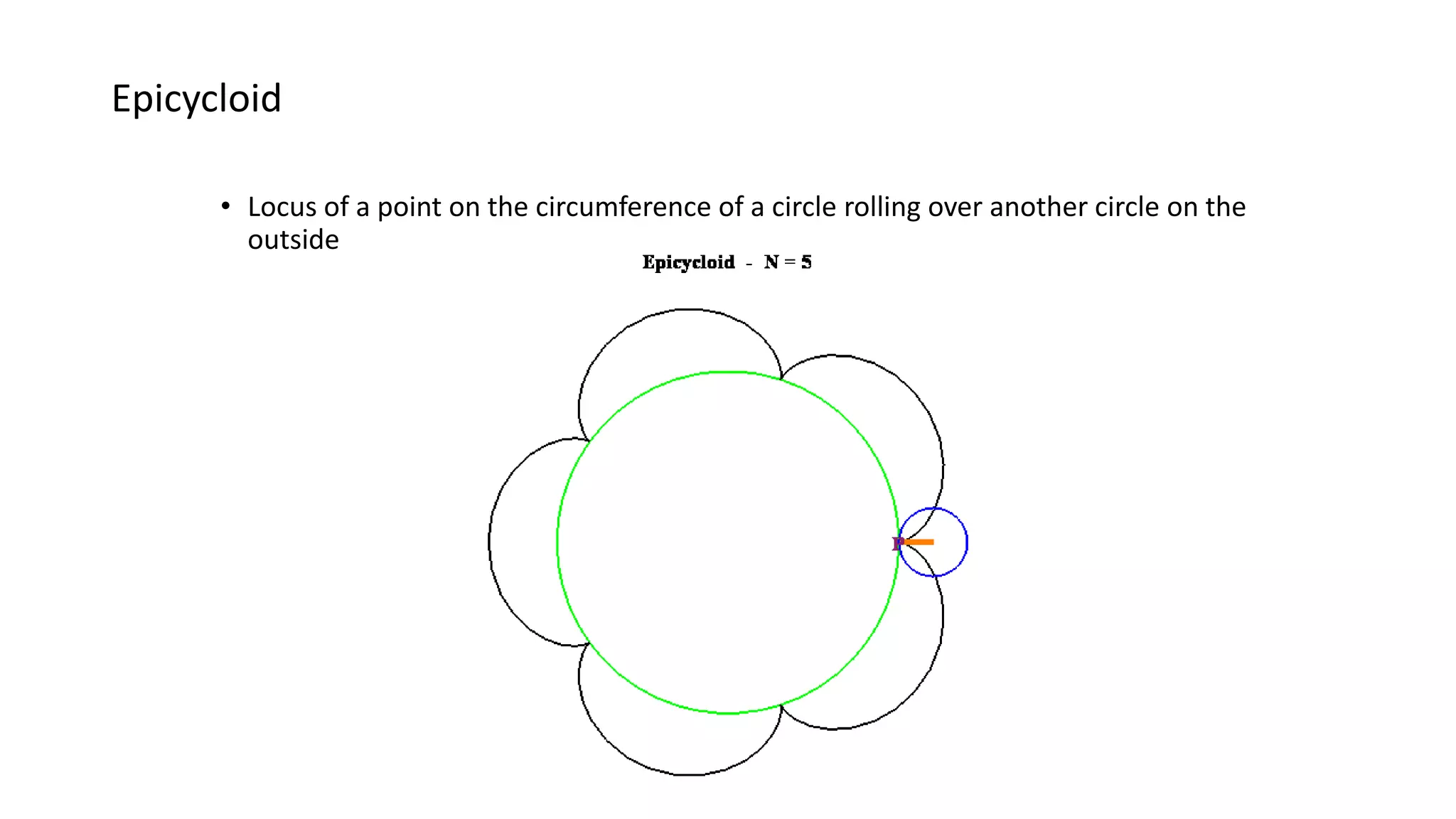
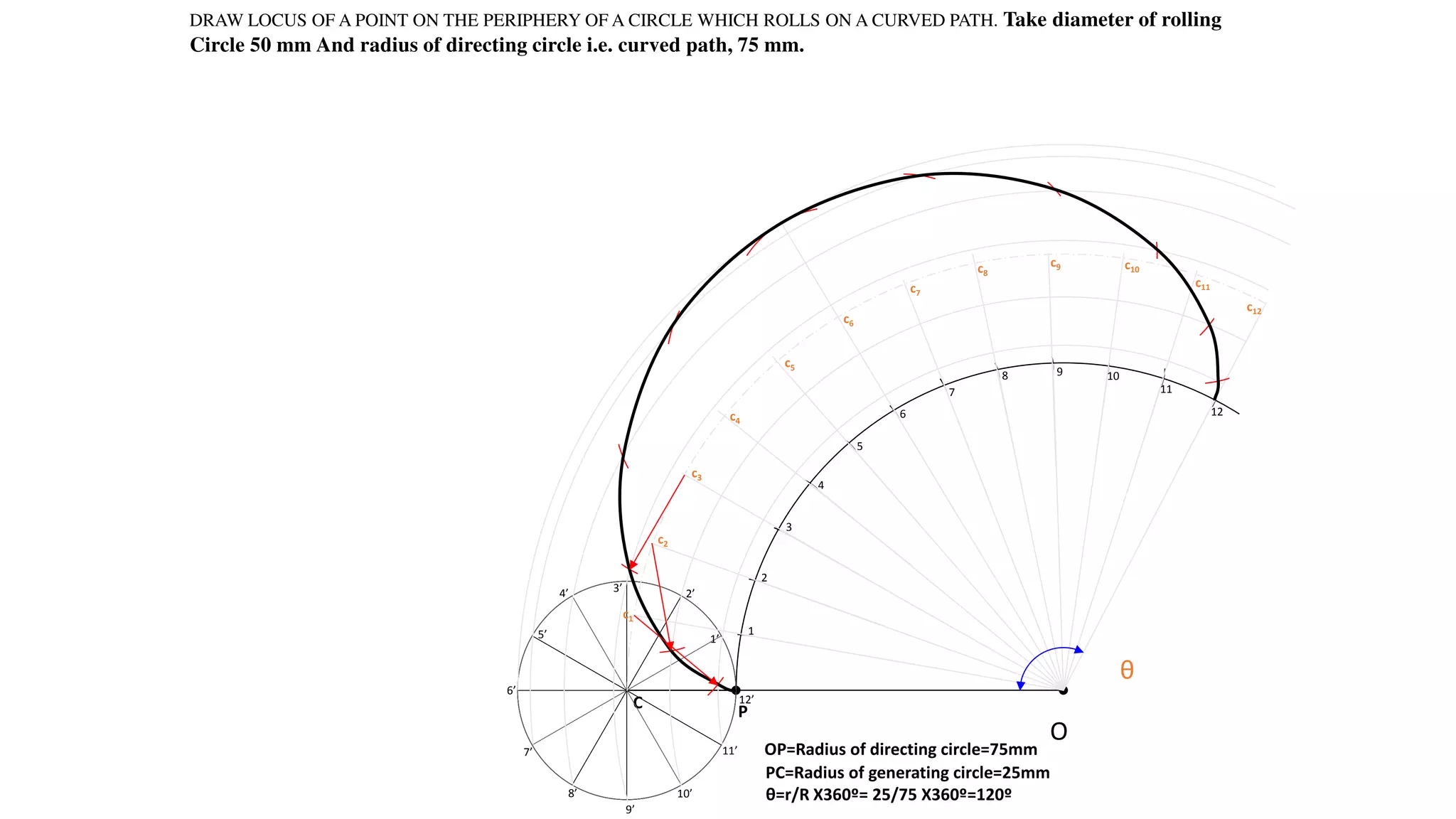
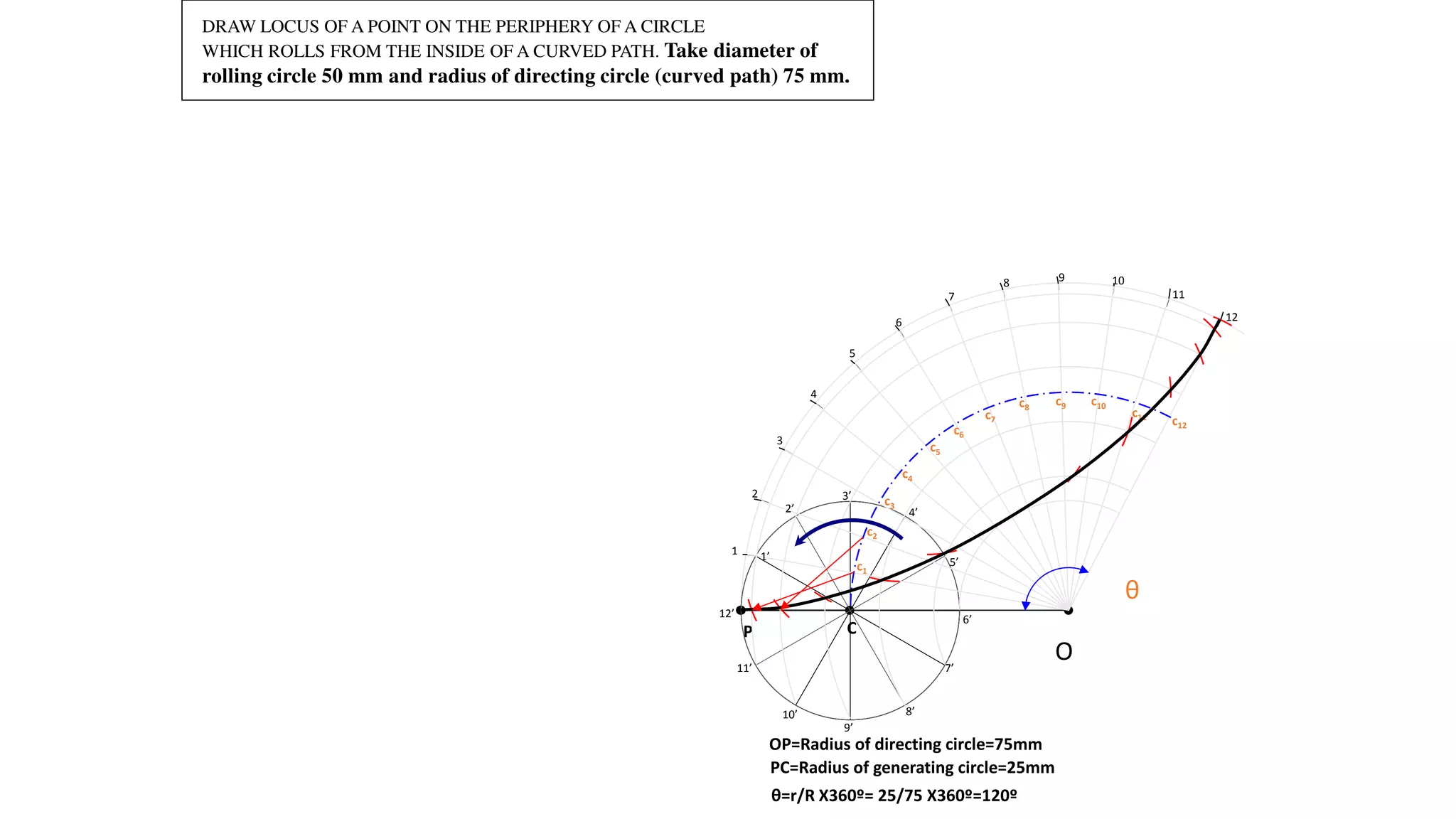
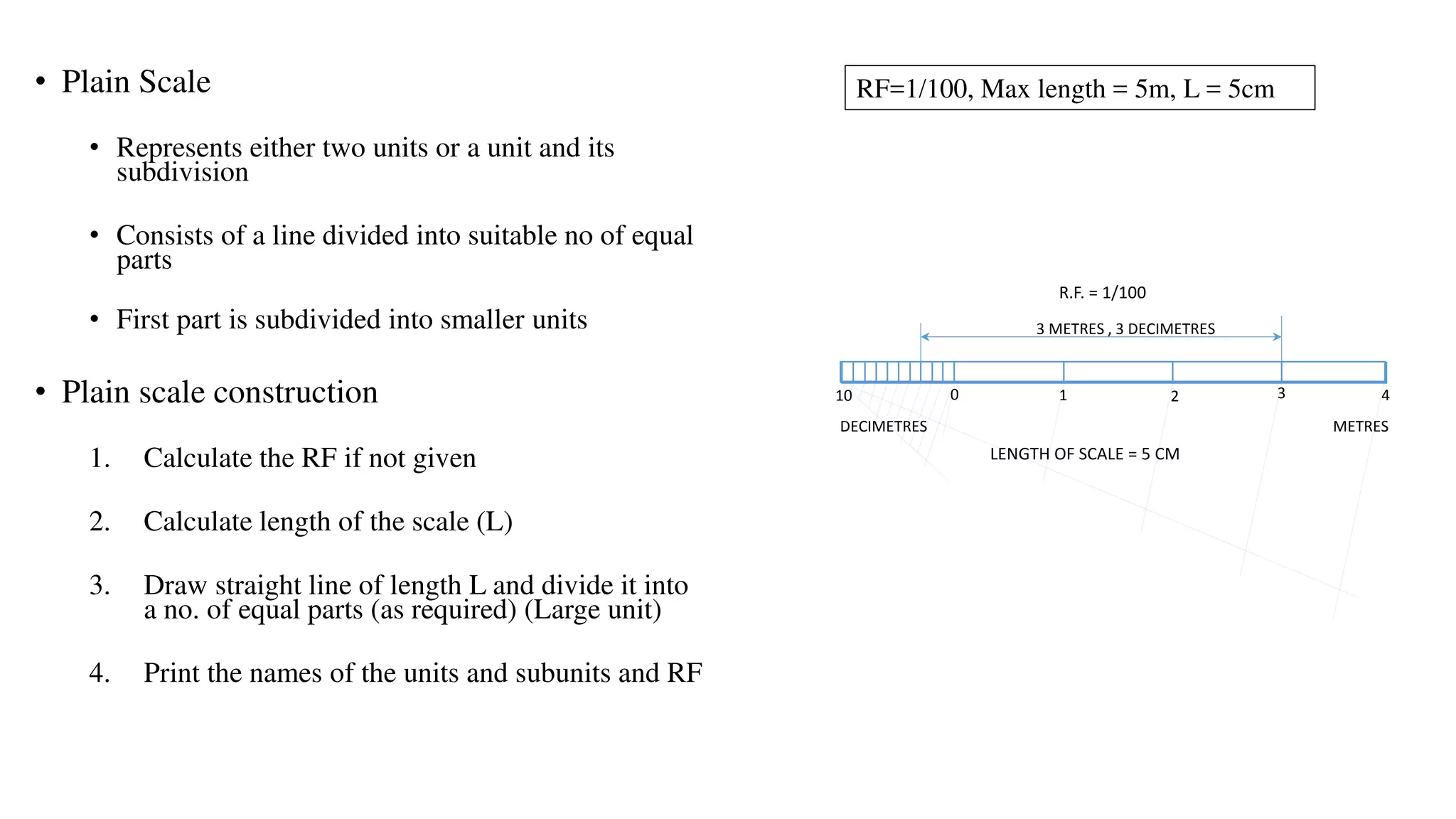
- Scales are used to represent large or small real-world dimensions on technical drawings by reducing or enlarging the measurements. - Standard scale ratios recommended by the Bureau of Indian Standards include 1:1, 1:2, 1:5, 1:10, 1:50, 1:100, 1:200, 1:1000, 1:2000, 1:5000, as well as enlarged scales like 50:1, 20:1, 10:1, 5:1, and 2:1. - Plain scales represent units and subdivisions using a line divided into equal parts, while diagonal scales represent units through their fractions using diagonally divided lines.

1. Scales

2. • Dimension of an object on drawing and on real object are not always same
• For the ease of reading and handling of the drawing of an object
• Dimension of large object is reduced
• Similarly small objects are drawn enlarged
• This reduction or enlargement creates a scale of that ratio
• Representative Factor (RF)
L w
L
• Suppose 2 Km is shown by 20 cm on the drawing
• Scale 1:10000
• RF = 1/10000

3. • Scale recommended by BIS (Bureau of Indian Standards)
• Full scale
1:1
• Reduced scale
1:2
1:5
1:10
1:50
1:100
1:200
1:1000
1:2000
1:5000
• Enlarged scale
50:1
20:1
10:1
5:1
2:1

4. • For constructing a scale, one must know
• RF of the scale
• The unit it is to represent
• Max length required to be measured
Length of scale (L) = RF X Max length required to be measured
• Types of scale
• Plain scale
• Diagonal scale
• Vernier scale
• Isometric scale
• Scale of chords
• Comparative scale

5. • Plain Scale
• Represents either two units or a unit and its
subdivision
• Consists of a line divided into suitable no of equal
parts
• First part is subdivided into smaller units
• Plain scale construction
1. Calculate the RF if not given
2. Calculate length of the scale (L)
3. Draw straight line of length L and divide it into
a no. of equal parts (as required) (Large unit)
4. Print the names of the units and subunits and RF
RF=1/100, Max length = 5m, L = 5cm
0 1 2 3 410
METRESDECIMETRES
R.F. = 1/100
LENGTH OF SCALE = 5 CM
3 METRES , 3 DECIMETRES

6. • Diagonal Scale
• Represents three units or a unit and its fraction upto second
place of decimal
• Consists of a line divided into suitable no of equal part
• First part is divided into smallest part by diagonals
• Principle of diagonal division
• To divide AB into 5 equal parts
• Draw BC perpendicular to AB
• Divide BC into 5 equal parts
• Draw line AC
• Draw lines 1- ’ , - ’ , - ’ ……
• From similar triangles
• 1- ’=AB/
• 2- ’= *AB/
A B
C
1’
’
’
’
2
3
4

7. Q 11: Construct a scale of R.F. 3:200 showing metres, decimetres and centimetres. The
scale should measure upto 6 metres. Show a distance of 4.37 metres.
L = 3/200*6 meters = 9 centimeters
0 1 2 3 4 510
0
10
DECIMETRES
CENTIMETRES
METRES
R. F. = 3/200
LENGTH OF SCALE = 9 CM
4.37 METRES

8. • Roulettes
• Curves generated by a fixed point on a curve rolling over another curve
without slipping
• Generating and directing curve
• Cycloid, Epicycloid, Hypocycloid and involute
• Important application in profile of gear teeth

9. Cycloid
• Locus of a point on the circumference of a circle rolling in a plane

10. Epicycloid
• Locus of a point on the circumference of a circle rolling over another circle on the
outside

11. Hypocycloid
• Locus of a point on the circumference of a circle rolling over another circle on the inside

12. P
C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 C11 C12
p1
p2
p3
p4
p5
p6
p7
p8
D
CYCLOIDDraw locus of a point on the periphery of a circle which rolls on straight line path. Take circle
diameter as 50 mm. Draw normal and tangent on the curve at a point 40 mm above the
directing line.
p9
p10
p11
p121
2
3
5
4
6
7
8
9
10
11
12

13. O
P
OP=Radius of directing circle=75mm
C
PC=Radius of generating circle=25mm
θ
θ=r/R X360º= 25/75 X360º=120º
1
2
3
4
5
6
7
8 9 10
11
12
’
’’’
’
’
’
’
’
’
’
’
c1
c2
c3
c4
c5
c6
c7
c8
c9 c10
c11
c12
DRAW LOCUS OF A POINT ON THE PERIPHERY OF A CIRCLE WHICH ROLLS ON A CURVED PATH. Take diameter of rolling
Circle 50 mm And radius of directing circle i.e. curved path, 75 mm.

14. O
P
OP=Radius of directing circle=75mm
C
PC=Radius of generating circle=25mm
θ
θ=r/R X360º= 25/75 X360º=120º
1
2
3
4
5
6
7
8 9 10
11
12
c2
c1
c3
c4
c5
c6
c7
c8
c9 c10
c11
c12
’
’
’
’
’
’
’
’
’
’
’
’
DRAW LOCUS OF A POINT ON THE PERIPHERY OF A CIRCLE
WHICH ROLLS FROM THE INSIDE OF A CURVED PATH. Take diameter of
rolling circle 50 mm and radius of directing circle (curved path) 75 mm.

15. Draw involute of a square of 25 mm sides
25 100
Involute: A spiral curve traced by a point on a chord unwinding from around a polygon or a circle

16. Draw Involute of a circle
1 2 3 4 5 6 7 8
P
P8
1
2
3
4
5
6
7
8
P3
P4
4 to p
P5
P7
P6
P2
P1
D
A