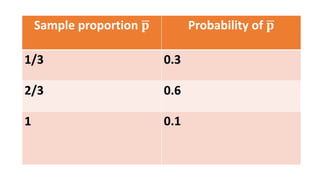
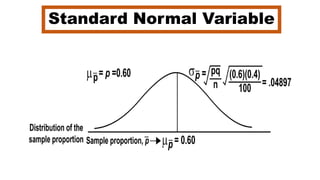
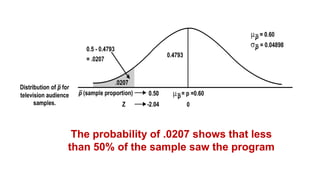
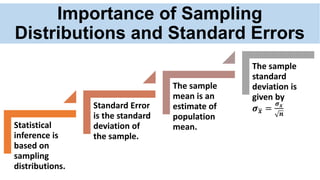
This document discusses sampling distributions and concepts related to proportions in statistics. It explains that the proportion of a characteristic in a sample (p) is a random variable whose distribution depends on the sample size (n). The mean (μp) of this sampling distribution is equal to the population proportion (p). It also defines the standard error of a proportion as the standard deviation of its sampling distribution. An example shows how to calculate the probability that a sample proportion is less than a value using the normal distribution. The key point is that sampling distributions allow inferences about populations based on sample statistics and their standard errors.

1. Dr. K. Prabhakar
Professor
Sampling Concepts

2. CONTENT
Normal
distribution of
𝒙
Sampling
distribution of
the proportion

3. Research in social
sciences is replete with
proportions
p (population
proportion) of having
certain characteristic
Sampling Distribution of Proportion

4. We know the population
parameters and we are
considering the sample statistic
from the population

5. Let us consider a population of N = 0, 7, 6, 7, 36
Containing three even numbers 0, 6, 36 and two odd numbers 7 and 7
The population proportion of even numbers is (which we may call as success),
µ p= 3/5 = 0.6
If we consider a sample size of n=3 and if we get the first three numbers
0,7,6, then the sample proportion of even numbers is 2/3 and denoted by 𝒑.
Thus 𝒑 is the sample statistic and p is the population parameter.
Sampling Distribution of Proportion

6. Ten samples of size n=3 may be drawn from population of N=5
The 𝒑 value of all 10 samples of 3 of even numbers proportions are,
2/3,1/3,2/3,2/3,1,2/3,1/3,2/3,1/3,2/3
Three of the ten proportions are 1/3; so the probability for 𝒑=1/3 is
3/10 or 0.3. Similarly, for 𝒑 =2/3 and 𝒑 =1 the respective
probabilities are 0.6 and 0.1
Sampling Distribution of Proportion

7. Sample proportion 𝐩 Probability of 𝐩
1/3 0.3
2/3 0.6
1 0.1

8. If the mean and standard deviation of these ten numbers
computed 0.6 and 0.2 are obtained. Thus 𝝁 𝒑 = 0.6 and 𝝈 𝒑 = 0.2.
The 𝝁 𝒑 symbol 𝝁 𝒑 represents the mean of the distribution of 𝒑.
Note 𝝁 𝒑 is equal to 0.6 and population proportion p is also 0.6. This
equality should be remembered the population proportion and the
mean of means of all sample proportion is the same i.e. 𝝁 𝒑= p.
Sampling Distribution of Proportion

9. To solve the
problems we use
the formulae,
•𝝁 𝒑 = p
•𝝈 𝒑 =
𝑝𝑞
𝑛

10. Standard Error of
Proportion

11. The symbol 𝝈 𝒑 is called the standard error of the proportion.
Let p be any given population proportion, and q= 1-p; then for sample size n
from a population of size N is given by
Thus in the example given where p=0.6, therefore q=(1-p)=0.4, n=3 and N=5,
we may compute
𝝈 𝒑 =
The value is a finite population multiplier is given by
𝑵−𝒏
𝑵−𝟏
. This will be very small
quantity in the case of social sciences with large samples and we may ignore the
component. Thus for the example given the 𝝈 𝒑 = 𝟎. 𝟔 × 𝟎. 𝟒/𝟑 ∗ 0.5 = 𝟎. 𝟐
𝑝𝑞
𝑛
𝑁 − 𝑛
𝑁 − 1

12. Sixty percent (p=0.60) of total television audience population watched a particular
program on Wednesday evening. What is the probability that in a random sample
of 100 viewers, less than 50% of the sample watched the programme?
Remark: In this problem we know the population proportion that is .60 or 60% and
we wanted to check the sample proportion. The random variable proportion µ 𝒑 =
p = 0.6.
• Please do remember the population proportion will be equal to sample proportion.
The standard error of 𝒑 is 𝝈 𝒑 =
.𝟔∗.𝟒
𝟏𝟎𝟎
=. 𝟎𝟒𝟖𝟗𝟕
Example

13. Standard Normal Variable
The general standard normal variable is given by,
z = Value of the Random Variable – Mean of the Random Variable
Standard Deviation of the random variable
The statistic 𝒑 is our random variable; thus z = ( 𝒑-µ 𝒑)/σ 𝒑
This formula please do commit to your memory.

14. Standard Normal Variable

15. The statistics is our random variable
•So, z = ( 𝒑-µ 𝒑)/σ 𝒑 = ( 𝒑−𝒑)/σ 𝒑
Thus, z = 0.50-0.60/.04897 = -2.04 as
shown in the diagram.

16. The probability of .0207 shows that less
than 50% of the sample saw the program

17. Why we need to
convert all measures to
standard normal
variable?

18. If two students are asked to measure heights of all
students in the class and report the results, one may
take a scale and measure the heights in inches and
other may use centimetres.
Both will come with a mean and standard
deviation expressed in the units measured
them.
Example

19. Who is
right?

20. Importance of Sampling
Distributions and Standard Errors
Statistical
inference is
based on
sampling
distributions.
Standard Error
is the standard
deviation of
the sample.
The sample
mean is an
estimate of
population
mean.
The sample
standard
deviation is
given by
𝝈 𝒙 =
𝝈 𝒙
𝒏

21. Dr. K. Prabhakar
Professor,
BS Abdur Rahman Crescent Institute of Science and Technology,
Vandalur-600048
Online Refresher Course
On
Research Methods & Data Analysis in HRM
Sampling Concepts