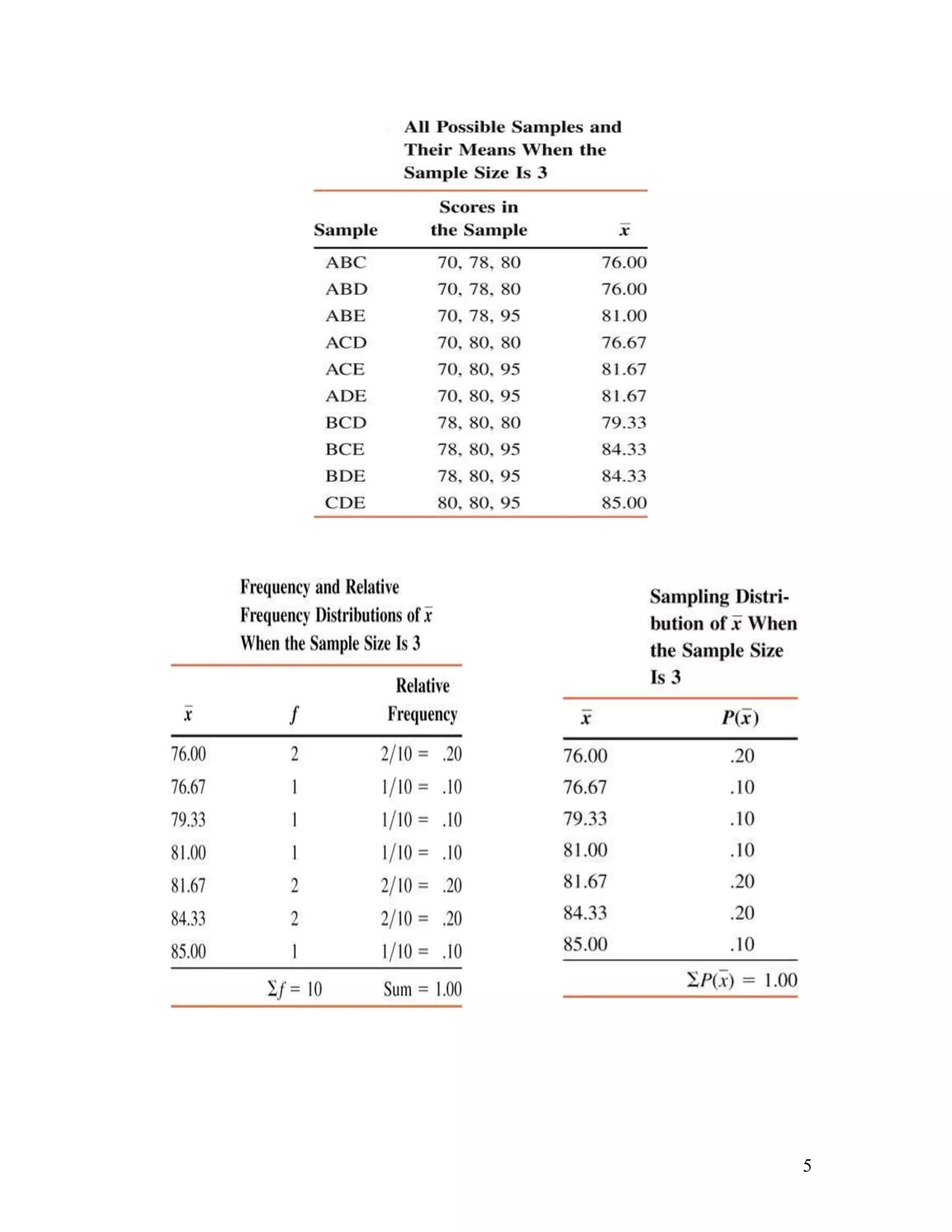
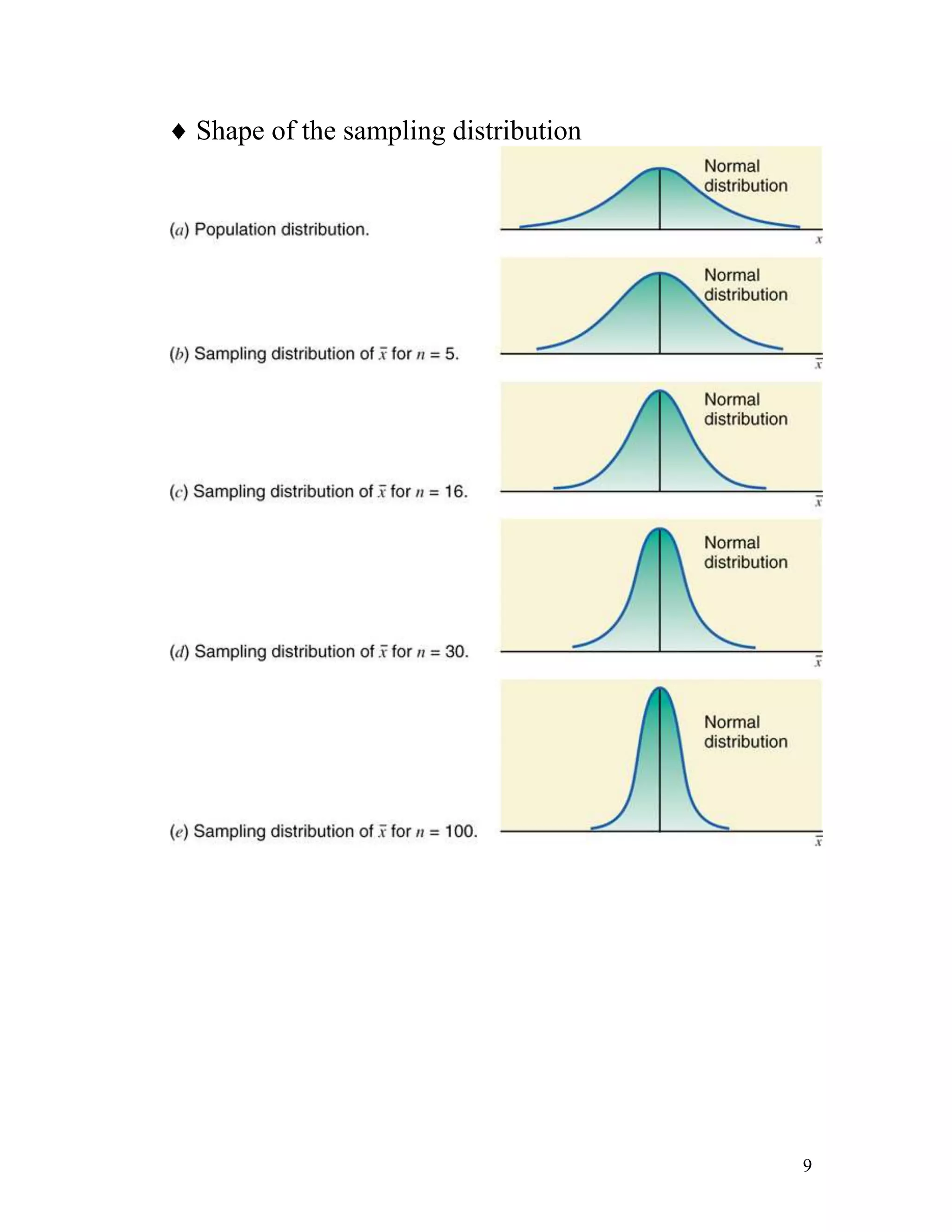
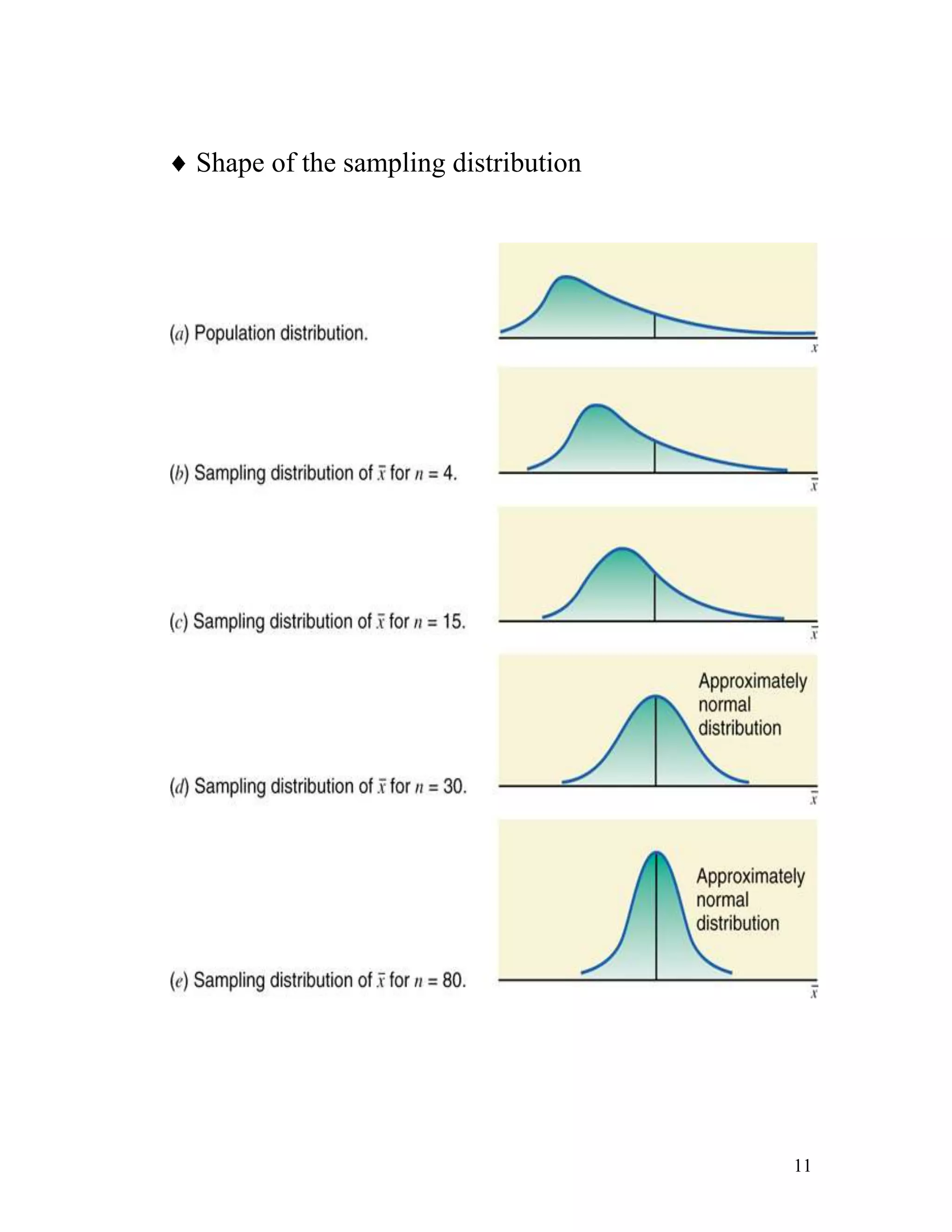
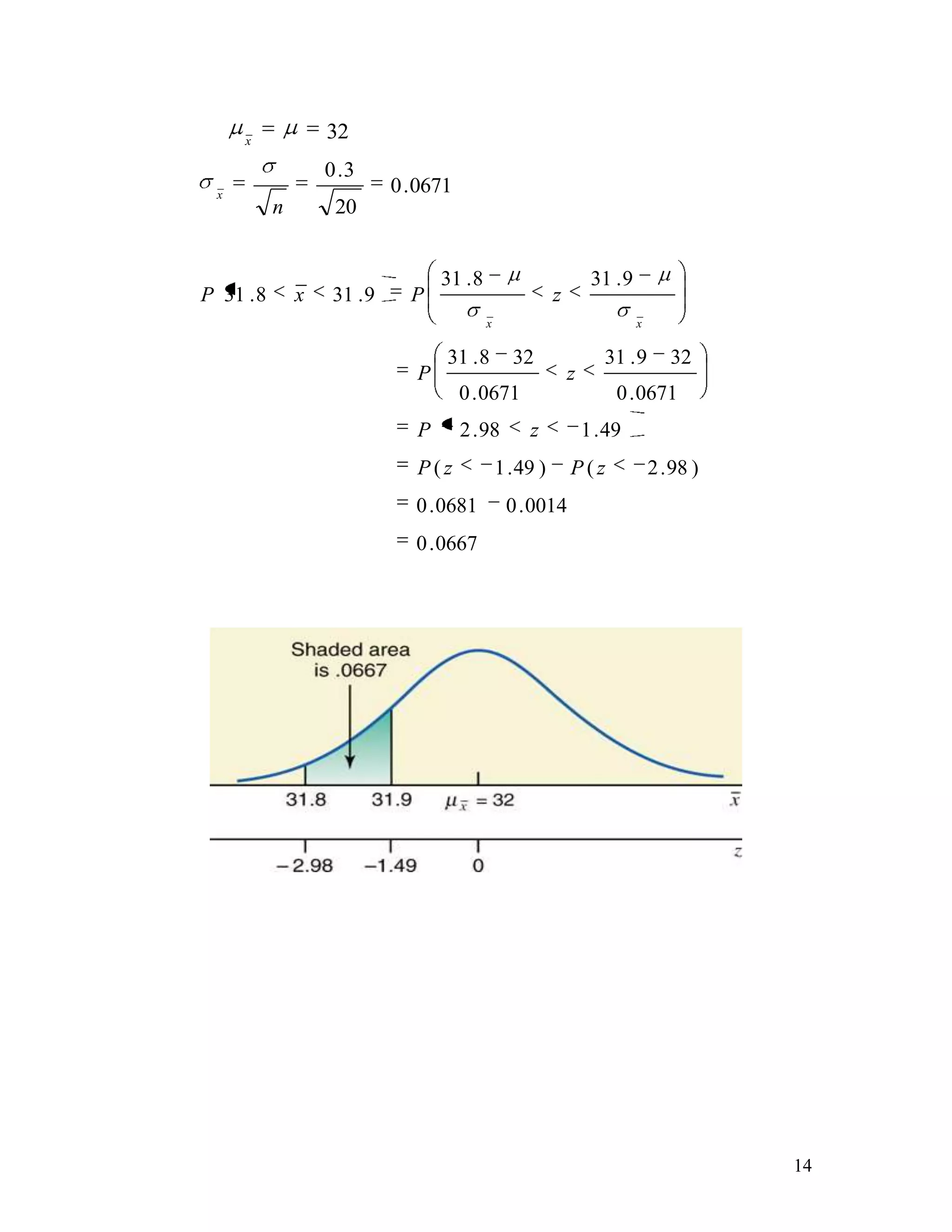
The document discusses sampling distributions and their properties. It defines key terms like population distribution, sampling distribution, sampling error, and sampling distribution of the mean. It presents formulas for calculating the mean and standard deviation of sampling distributions of the mean and proportion. Several examples are provided to demonstrate calculating probabilities related to sampling distributions.

1. CHAPTER 6SAMPLING DISTRIBUTIONOBJECTIVES:After completing this chapter, student should be able to:Form a sampling distribution for a mean and proportion based on a small, finite population.Understand that a sampling distribution is a probability distribution for a sample statistic.Present and describe the sampling distribution of sample means and the central limit theorem.Explain the relationship between the sampling distributions with the central limit theorem.Compute, describe and interpret z-scores corresponding to known values of Compute z-scores and probabilities for applications of the sampling distribution of sample means and sample proportions.1.0POPULATION AND SAMPLING DISTRIBUTION1.1Population DistributionDefinition: The probability distribution of the population data.Example 1:Suppose there are only five students in an advanced statistics class and the midterm scores of these five students are:7078808095Let x denote the score of a student.Mean for Population:Standard Deviation for Population:1.2Sampling Distribution Definition: The probability distribution of a sample statistic.Sample statistic such as median, mode, mean and standard deviation1.2.1Sampling Distribution of Mean SampleDefinition: The sampling distribution of is a distribution obtained by using the means computed from random samples of a specific size taken from a population.Example 2: Reconsider the population of midterm scores of five students given in example 1.Let say we draw all possible samples of three numbers each and compute the mean.Total number of samples = 5C3 =Suppose we assign the letters A, B, C, D and E to scores of the five students, so thatA = 70,B = 78,C=80,D = 80, E = 95Then the 10 possible samples of three scores each areABC, ABD, ABE, ACD, ACE, ADE, BCD, BCE, BDE, CDESampling ErrorSampling error is the difference between the value of a sample statistic and the value of the corresponding population parameter. In the case of mean,Sampling error =Mean () for the Sampling Distribution of:Based on example 2,“The mean of the sampling distribution of is always equal to the mean of the population”Standard Deviation () for the Sampling Distribution of :Formula 1 where: is the standard deviation of the population n is the sample sizeThis formula is used when Formula 2When N is the population size where is the finite population correction factor This formula is used whenThe spread of the sampling distribution of is smaller than the spread of the corresponding population distribution, .The standard deviation of the sampling distribution of decreases as the sample size increase.The standard deviation of the sample means is called the standard error of the mean.Sampling from a Normally Distributed PopulationThe shape of the sampling distribution of is normal, whatever the value of n.Shape of the sampling distributionSampling from a Not Normally Distributed Population Most of the time the population from which the samples are selected is not normally distributed. In such cases, the shape of the sampling distribution of is inferred from central limit theorem.Central limit theorem:for a large sample size, the sampling distribution of is approximately normal, irrespective of the population distribution.the sample size is usually considered to be large if.Shape of the sampling distributionApplications of the Sampling Distribution of The z value for a value of is calculated as:Example 3:In a study of the life expectancy of 500 people in a certain geographic region, the mean age at death was 72 years and the standard deviation was 5.3 years. If a sample of 50 people from this region is selected, find the probability that the mean life expectancy will be less than 70 years.Solution: need correction factorExample 4:Assume that the weights of all packages of a certain brand of cookies are normally distributed with a mean of 32 ounces and a standard deviation of 0.3 ounce. Find the probability that the mean weight,of a random sample of 20 packages of this brand of cookies will be between 31.8 and 31.9 ounces.Solution:Although the sample size is small (), the shape of the sampling distribution of is normal because the population is normally distributed. 57150047625Example 5:A Bulletin reported that children between the ages of 2 and 5 watch an average of 25 hours of television per week. Assume the variable is normally distributed and the standard deviation is 3 hours. If 20 children between the ages of 2 and 5 are randomly selected, find the probability that the mean of the number of hours they watch television will be:greater than 26.3 hours.less than 24 hoursbetween 24 and 26.3 hours.Solution:greater than 26.3 hours less than 24 hoursbetween 24 and 26.3 hoursORRemember!Sometimes you have difficulty deciding whether to use or The formula should be used to gain information about a sample mean.The formula is used to gain information about an individual data value obtained from the population.Example 6: The average number of pounds of meat that a person consumes a year is 218.4 pounds. Assume that the standard deviation is 25 pounds and the distribution is approximately normal.Find the probability that a person selected at random consumes less than 224 pounds per year.If a sample of 40 individuals selected, find the probability that the mean of the sample will be less than 224 pounds per year.Solution:The question asks about an individual person . ,The question concerns the mean of a sample with a size of 40 , POPULATION AND SAMPLE PROPORTIONSFormula for:Population proportionSample proportionWhere N = total number of element in the population n = total number of element in the sample X = number of element in the population that possess a specific characteristic x = number of element in the sample that possess a specific characteristicExample 7Suppose a total of 789 654 families live in a city and 563 282 of them own homes. A sample of 240 families is selected from the city and 158 of them own homes. Find the proportion of families who own homes in the population and in the sample.Solution:The proportion of all families in this city who own homes isThe sample proportion is 2.1Sampling Distribution of Example 8Boe Consultant Associates has five employees. Table below gives the names of these five employees and information concerning their knowledge of statistics. Where: p = population proportion of employees who know statistics Let say we draw all possible samples of three employees each and compute the proportion.Total number of samples = 5C3 = Mean of the sample proportion: Standard deviation of the sample proportion:If , then use formulaIf , then use formula where p = population proportion q = 1 – p n = sample sizeExample 9Based on example Boe Consultant Associates,Shape of the sampling distribution of According to the central limit theorem, the sampling distribution of is approximately normal for a sufficiently large sample size.In the case of proportion, the sample size is considered to be sufficiently large if np > 5 and nq > 5Example 10A binomial distribution has p = 0.3. How large must sample size be such that a normal distribution can be used to approximate sampling distribution of .Solution:2.2Applications Of The Sampling Distribution of z value for a value of Example 11:The Dartmouth Distribution Warehouse makes deliveries of a large number of products to its customers. It is known that 85% of all the orders it receives from its customers are delivered on time.Find the probability that the proportion of orders in a random sample of 100 are delivered on time:less than 0.87between 0.81 and 0.88Find the probability that the proportion of orders in a random sample of 100 are not delivered on time greater than 0.1.Solution:p = 85% = 0.85 np = 85 >5q = 1-p = 0.15nq = 15 > 5n = 100 approximately normali. ii.proportion are not delivered on time = pExample 12The machine that is used to make these CDs is known to produce 6% defective CDs. The quality control inspector selects a sample of 100 CDs every week and inspects them for being good or defective. If 8% or more of the CDs in the sample are defective, the process is stopped and the machine is readjusted. What is the probability that based on a sample of 100 CDs the process will be stopped to readjust the mashine?Solution:p = 6% = 0.06 np = 6 >5q = 1-p = 0.94nq = 94 > 5n = 100 approximately normalP(process is stopped)EXERCISESGiven a population with mean, µ = 400 and standard deviation, σ = 60.If the population is normally distributed, what is the shape for the sampling distribution of sample mean with random sample size of 16If we do not know the shape of the population in 1(a), Can we answer 1(a)? Explain.Can we answer 1(a) if we do not know the population distribution but we have been given random sample with size 36? Explain.A random sample with size, n = 30, is obtained from a normal distribution population with µ = 13 and s = 7.What are the mean and the standard deviation for the sampling distribution of sample mean.What is the shape of the sampling distribution? Explain.Calculate¯¯¯P ( x P ( x P ( x Given a population size of 5000 with standard deviation 25, Calculate the standard error of mean sample for:n = 300n = 100 XGiven X ~ N (5.55, 1.32). If a sample size of 50 is randomly selected, find the sampling distribution for ¯. (Hint: Give the name of distribution, mean and variance).Then, Calculate:P ( 5.25 ≤ X ≤ 5.90)P (5.45 ≤ X ≤ 5.75)XXXGiven ¯ ~ N (5, 16). Find the value of:P ( ¯ > 3)P( -4 64 units from a population size of 125 is randomly selected with mean 105 and variance 289, Find:Xthe standard error of the sampling distribution aboveP( -4 The serving time for clerk at the bank counter is normally distributed with mean 8 minutes and standard deviation 2 minutes. If 36 customers is randomly selected:¯a) Calculate σxb) The probability that the mean of serving time of a clerk at the bank counter is between 7.7 minutes and 8.3 minutesThe workers at the walkie-talkie factory received salary at an average of RM3.70 per hour and the standard deviation is RM0.80. If a sample of 100 is randomly selected, find the probability the mean of sample is:at least RM 3.50 per hourbetween RM 3.20 and R3.60 per hour1,000 packs of pistachio nut have been sent to one of hyper supermarket in Puchong. The weight of pistachio nut packs is normally distributed with mean 99.3g and standard deviation is 1.8g.If a random sample with 300 packs of pistachio nut is selected, find the probability that the mean of the sample will be between 99.2g and 99.5g.Find the probability that mean of sample 300 packs of pistachio nut is between 99.2g and 99.5g with delivery of2,000 packs5,000 packsAn average age of 1500 staffs Tebrau Co. Limited is 38 years old with standard deviation 6.2 years old. If the company selects 50 staffs at random, Do we need correction factor in this situation? Justify your answer.Find the probability of average age for the group of this staff is between 35 and 40 years old.A research has been conducted by an independent research committee about the efficiency of wire harness, A12-3 production at the P.Tex Industries Sdn. Bhd. An average number of wire harness that has been produced a day is 60 pieces with standard deviation 10. A random sample of 90 pieces of wire harness is selected.Find mean and standard error for the wire harness that has been produced a day.Find the probability of wire harness that can be produced in a day is between 58 pieces and 62 pieces. A test of string breaking strength that has been produced by Z factory shows that the strength of string is only 60%. A random sample of 200 pieces of string is selected for the test.State the shape of sampling distributionCalculate the probability of string strength is at lest 42% Mr. Jay is a teacher at the Henry Garden School. He has conducted a research about bully case at his school. 61.6% students said that they are ever being a bully victim. A random sample of 200 students is selected at random. Find the proportion of bully victim is between 60% and 66%more than 64%The information given below shows the response of 40 college students for the question, “Do you work during semester break time?” (The answer is Y=Yes or N=No). N N Y N N Y N Y N Y N N Y N Y Y N N N Y N Y N N N N Y N N Y Y N N N Y N N Y N N If the proportion fo population is 0.30,Find the proportion of sampling for the college student who works during semester break.Calculate the standard error for the proportion in (a).A credit officer at the Tiger Bank believes that 25% from the total credit card users will not pay their minimum charge of credit card debt at the end of every month. If a sample 100 credit card user is randomly selected:What is the standard error for the proportion of the customer who does not pay their minimum charge of credit card debt at the end of every month?Find the probability that the proportion of customer in a random sample of 100 do not pay their minimum charge of credit card debt:less than 0.20more than 0.30What is the consequence of the incremental in population size toward the probability value on the 6(b)?