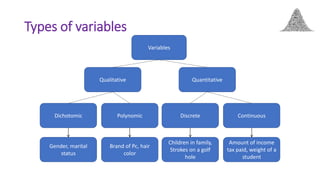
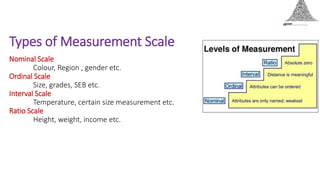
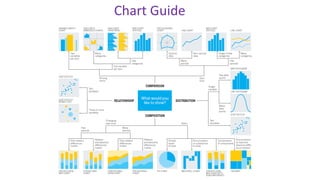
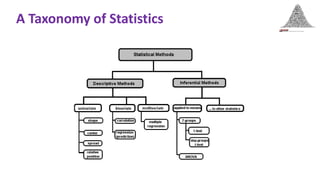
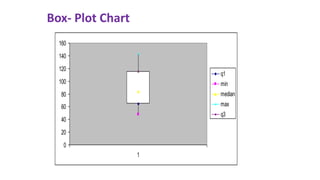
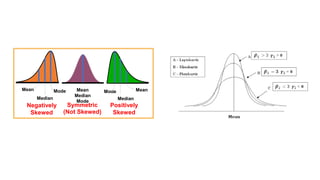
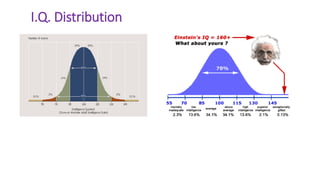
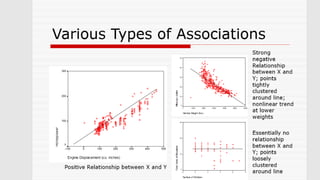
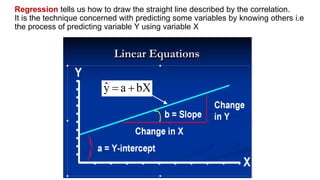
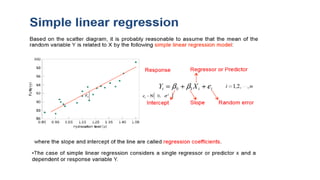
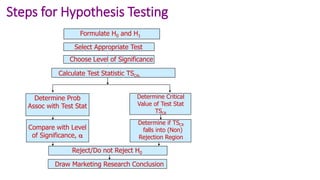
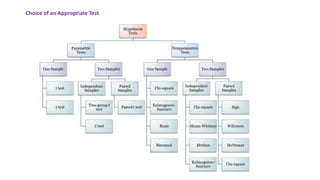
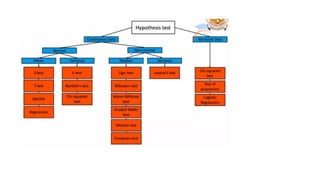
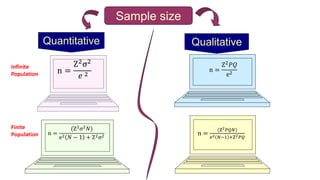
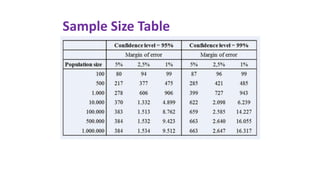
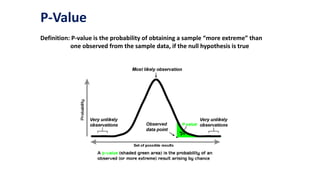
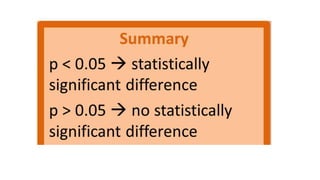
This document provides an overview of statistical methods used in research. It discusses descriptive statistics such as frequency distributions and measures of central tendency. It also covers inferential statistics including hypothesis testing, choice of statistical tests, and determining sample size. Various types of variables, measurement scales, charts, and distributions are defined. Inferential topics include correlation, regression, and multivariate techniques like multiple regression and factor analysis.