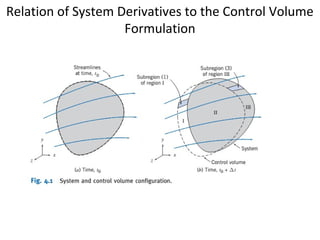
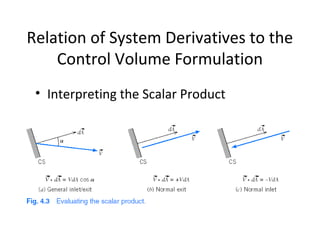
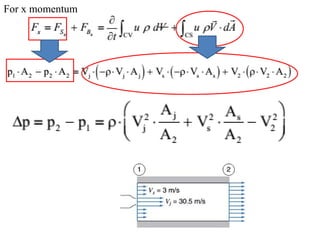
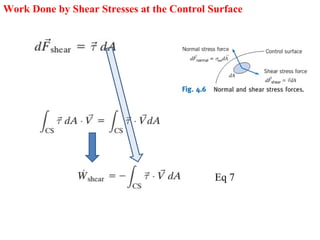
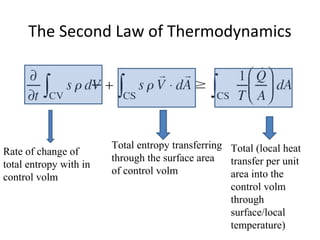
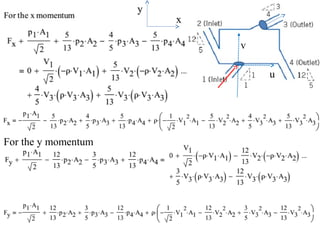
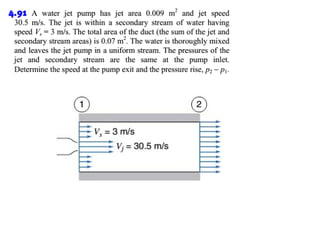
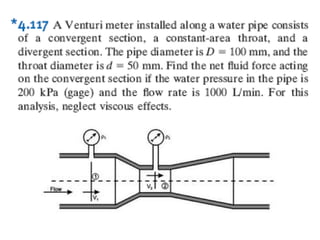
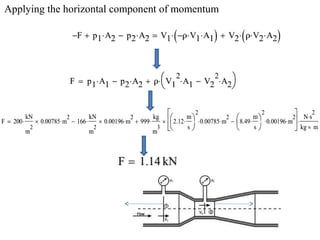
1. The document discusses several fundamental equations in fluid mechanics, including conservation of mass, momentum, energy, and angular momentum for control volumes. 2. Key equations presented include the Reynolds transport theorem, Bernoulli equation, and equations for conservation of mass, momentum, energy, and angular momentum derived using the transport theorem. 3. Examples are provided to demonstrate applying the conservation equations to problems involving steady and unsteady, compressible and incompressible flow.

1. All problems except the followings
Chapter 2
•45, 46, 48-52, 58, 63-65, 71
Chapter 3
•After 50

2. Introduction to Fluid Mechanics
Chapter 4
Basic Equations in Integral Form
for a Control Volume

3. Main Topics
1. Basic Laws for a System
2. Relation of System Derivatives
to the Control Volume Formulation
3. Conservation of Mass
4. Momentum Equation for
Inertial Control Volume
5. Momentum Equation for Inertial Control
Volume with Rectilinear Acceleration
6. The Angular-Momentum Principle
7. The First Law of Thermodynamics
8. The Second Law of Thermodynamics

4. Relation of System Derivatives to the
Control Volume Formulation
• Extensive and Intensive Properties
Eq 1

5. Relation of System Derivatives to the Control Volume
Formulation

6. Relation of System Derivatives to the
Control Volume Formulation
• Reynolds Transport Theorem
Eq 2
Physical Interpretation ??

7. is the rate of change of the system extensive property N. For example,
if N= , we obtain the rate of change of momentum
is the rate of change of the amount of property N in the control
volume. The term computes the instantaneous value
of N in the control volume ( is the instantaneous mass in
the control volume). For example, if then and
computes
the instantaneous amount of momentum in the control volume.
is the rate at which property N is exiting the surface of the control
volume. computes the rate of mass transfer leaving
across control surface area element ; multiplying by η computes
the rate of flux of property N across the element; and integrating
therefore computes the net flux of N out of the control volume. For
example, if N= , then η = and
computes the net
flux of momentum out of the control volume.

8. Relation of System Derivatives to the
Control Volume Formulation
• Interpreting the Scalar Product

9. Conservation of Mass
• Basic Law, and Transport Theorem

10. Conservation of Mass (continuity
equation)

11. Conservation of Mass
• Incompressible Fluids
Steady, Compressible Flow

12. Momentum Equation for
Inertial Control Volume
• Basic Law, and Transport Theorem

13. Momentum Equation for
Inertial (homogeneous motion, no
acceleration) Control Volume
• Special Case: Control Volume Moving with
Constant Velocity
xyz →coordinate system of control volume
Velocity must be measured with respect to controlled volume

14. Momentum Equation for
Inertial Control Volume
u,v, w are only the scalar components, no sign involved

16. Assumptions: 1) Incompressible flow 2) Uniform flow
For the mass equation

17. For the y momentum
u
v
x
y

19. Basic equation: Continuity, and momentum flux in x direction
Assumptions: 1) Steady flow 2) Incompressible flow CV 3) Uniform
flow

20. For x momentum

22. Basic Laws for a System
• The First Law of Thermodynamics
the rate of heat transfer, Q, is positive
when heat is added to the system
from the surroundings; the rate of work,
W, is positive when work is done by the
system on its surroundings.
Eq 1
Eq 2
Eq 3

23. The First Law of Thermodynamics
• Basic Law, and Transport Theorem
From eq 1 and Reynold Transport Theorem
Eq 4

24. Work Involves
 Shaft Work
 Work by normal Stresses
at the Control Surface
 Work by Shear Stresses at
the Control Surface
 Other Work
Eq 5

25. Since the work out across the boundaries of the control volume is the
negative of the work done on the control volume, the total rate of work
out of the control volume due to normal stresses is
Work Done by Normal Stresses at the
Control Surface
work done on the
control volume
Eq 6

26. Work Done by Shear Stresses at the Control Surface
Eq 7

27. Control Volume Equation
From eq 1, 4, 5, 6,7
Rearranging this equation, we obtain
Since ρ=1/ν, where ν is specific volume, then
Eq 8

28. The First Law of Thermodynamics
From and Eq 8
h
Example 4.16, 4.17

30. Assumptions: 1) Adiabatic
2) No work
3) Neglect KE
4) Uniform properties at exit
5) Ideal gas
Continuity eq
First Law of Thermodynamics for a CV

31. From continuity
From the 1st law
For air

32. Hence

33. The Second Law of Thermodynamics
dA
A
Q
CS T
AdV
CS
sd
CV
s
t






∫≥








⋅∫+∀∫
∂
∂ 1
ρρ
.
At time t0
eq1
eq2
eq3
From 1, 2 ,3

34. The Second Law of Thermodynamics
Rate of change of
total entropy with in
control volm
Total entropy transferring
through the surface area
of control volm
Total (local heat
transfer per unit
area into the
control volm
through
surface/local
temperature)

35. Momentum Equation for Inertial Control Volume
• Special Case: Bernoulli Equation
1. Steady Flow
2. No Friction
3. Flow Along a Streamline
4. Incompressible Flow
A
B

37. Bernoulli equation and x momentum

38. Applying Bernoulli between inlet and throat

39. Applying the horizontal component of momentum

40. The Angular-Momentum Principle
• Basic Law, and Transport Theorem
From Transport Theorem

41. The Angular-Momentum Principle
all the torques
that act on the
control volume. rate of change of angular momentum
within the control volume + the net rate of
flux of angular momentum from the
control volume.