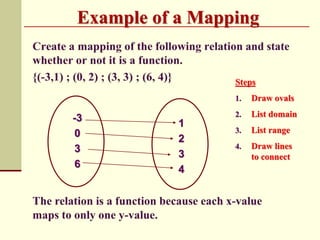
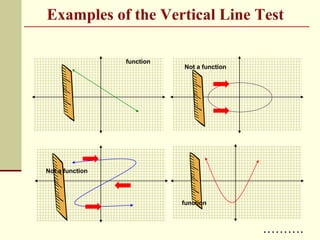
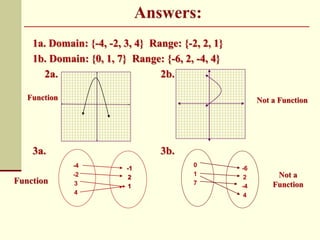
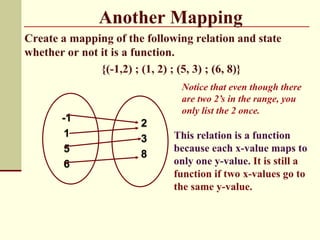
The document contains notes and examples about functions and relations. It defines functions and relations, and shows how to determine if a relation is a function using the vertical line test. Examples demonstrate evaluating functions for given inputs and writing the outputs in set notation. Steps are provided for mapping relations and identifying if they are functions. Practice problems have students substitute values into functions and write the outputs.

1. January 9, 2015
Today:

3. Vocabulary

5. x
y
1-1
(0,4)
(4,0)
-2 Time
Height/ft.

6. The Cost of a Phone Call
y = .16x

7. What is a Relation?
{ (1,16) ; (2,32) ; (3,48) ; (4,64) }

9. Example 1:

11. Functions: A Short Video

13. Example of a Mapping
Steps
1. Draw ovals
2. List domain
3. List range
4. Draw lines
to connect
-3
0
3
6
1
2
3
4

14. Create a mapping of the following relation and state
whether or not it is a function.
{(-4,-1) ; (-4, 0) ; (5, 1) ; (3, 9)}
-4
5
3
-1
0
1
9

15. Using the Vertical Line Test
Use the vertical line test to check
if the relation is a function only if
the relation is already graphed.
1. Hold a straightedge (pen, ruler,
etc) vertical to your graph.
2. Drag the straightedge from left
to right on the graph.
3. If the straightedge intersects
the graph once in each spot ,
then it is a function.
4. If the straightedge intersects the
graph more than once in any
spot, it is not a function.
A function!
……….

16. function
function
Not a function
Not a function
……….

17. Function Rules f(x)..g(x)..h(x)

18. ……….

20. y = -3x + 2
y = -3(-1) + 2
y = 3 + 2
y = 5

22. 1a. Domain: {-4, -2, 3, 4} Range: {-2, 2, 1}
1b. Domain: {0, 1, 7} Range: {-6, 2, -4, 4}
2a. 2b.
3a. 3b.
Function Not a Function
-4
-2
3
4
-1
2
1
0
1
7
-6
2
-4
4
Not a
Function

23. ……….

24. Practice
Steps
1. Sub in each domain value in one @ a time.
2. Solve for y in each
3. List y values in braces.

25. y = 3x + 1
y = 3(-4) + 1
y = -12 + 1
y = -11
y = 3x + 1
y = 3(0) + 1
y = 0 + 1
y = 1
Ans. { -11, 1, 7}
y = 3x + 1
y = 3(2) + 1
y = 6 + 1
y = 7
y = -2x + 3
y = -2(-5) + 3
y = 10 + 3
y = 13
y = -2x + 3
y = -2(-2) + 3
y = 4 +3
y = 7
y = -2x + 3
y = -2(6) + 3
y = -12 +3
y = -9
1.
2.