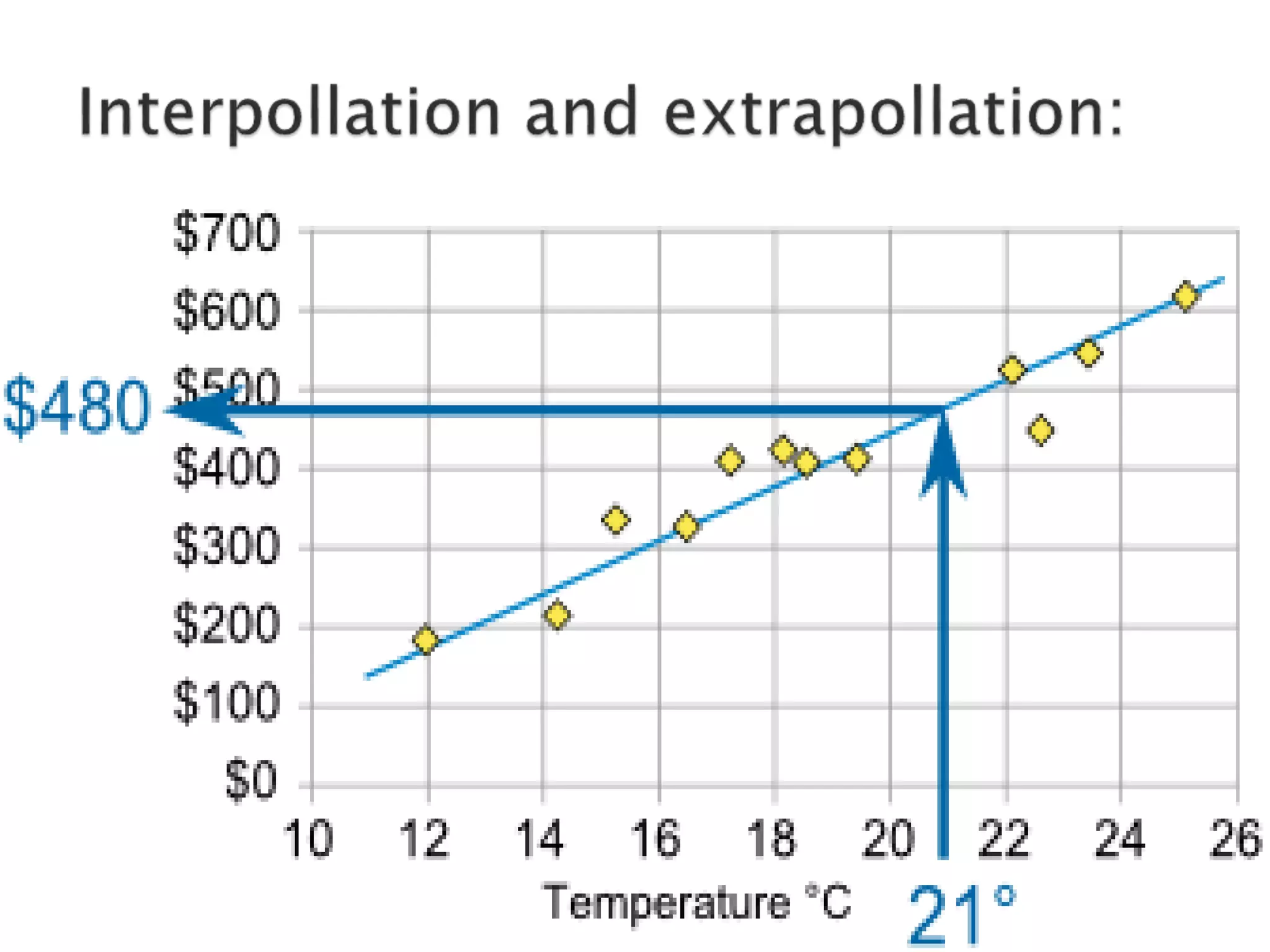
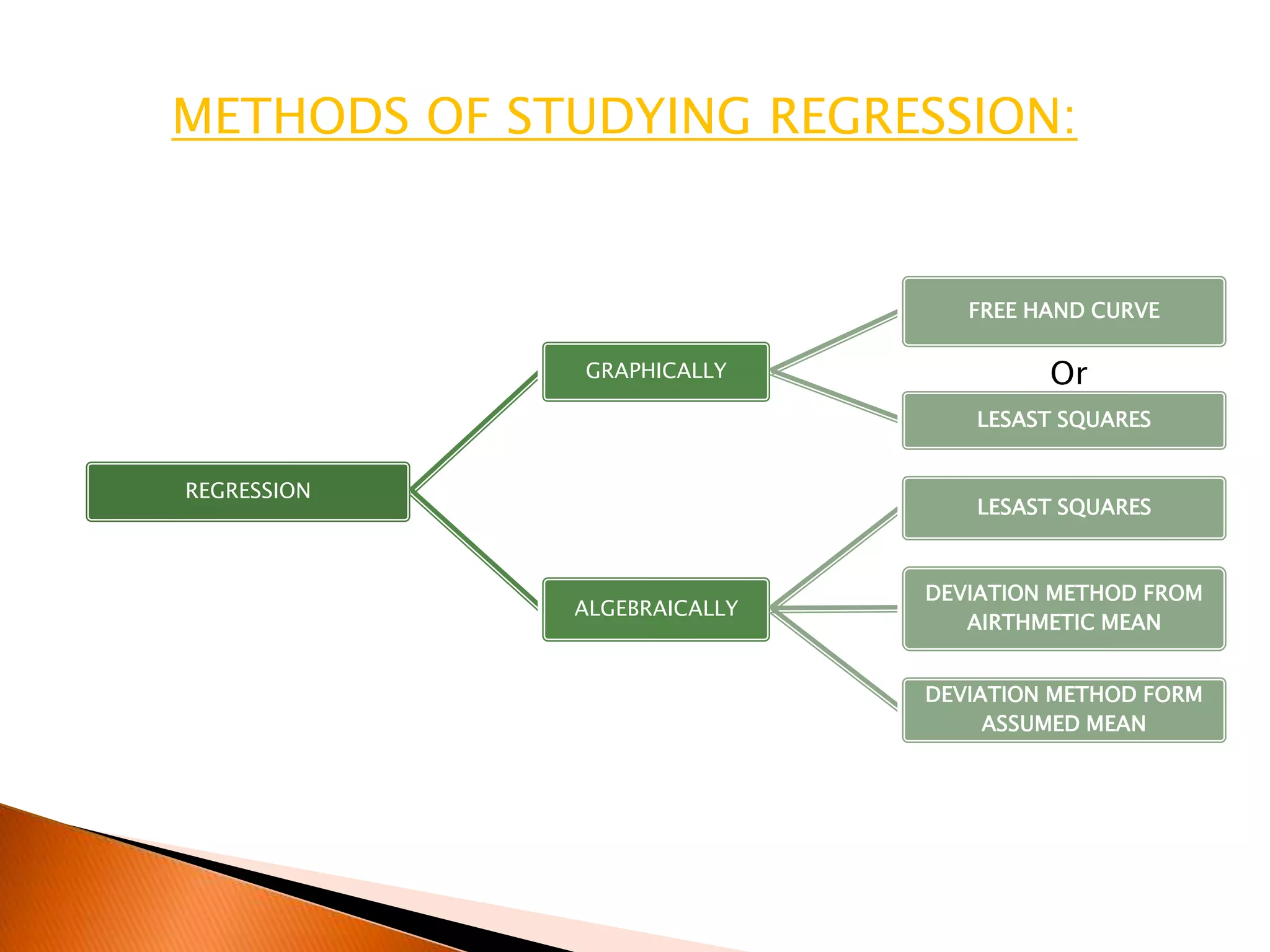
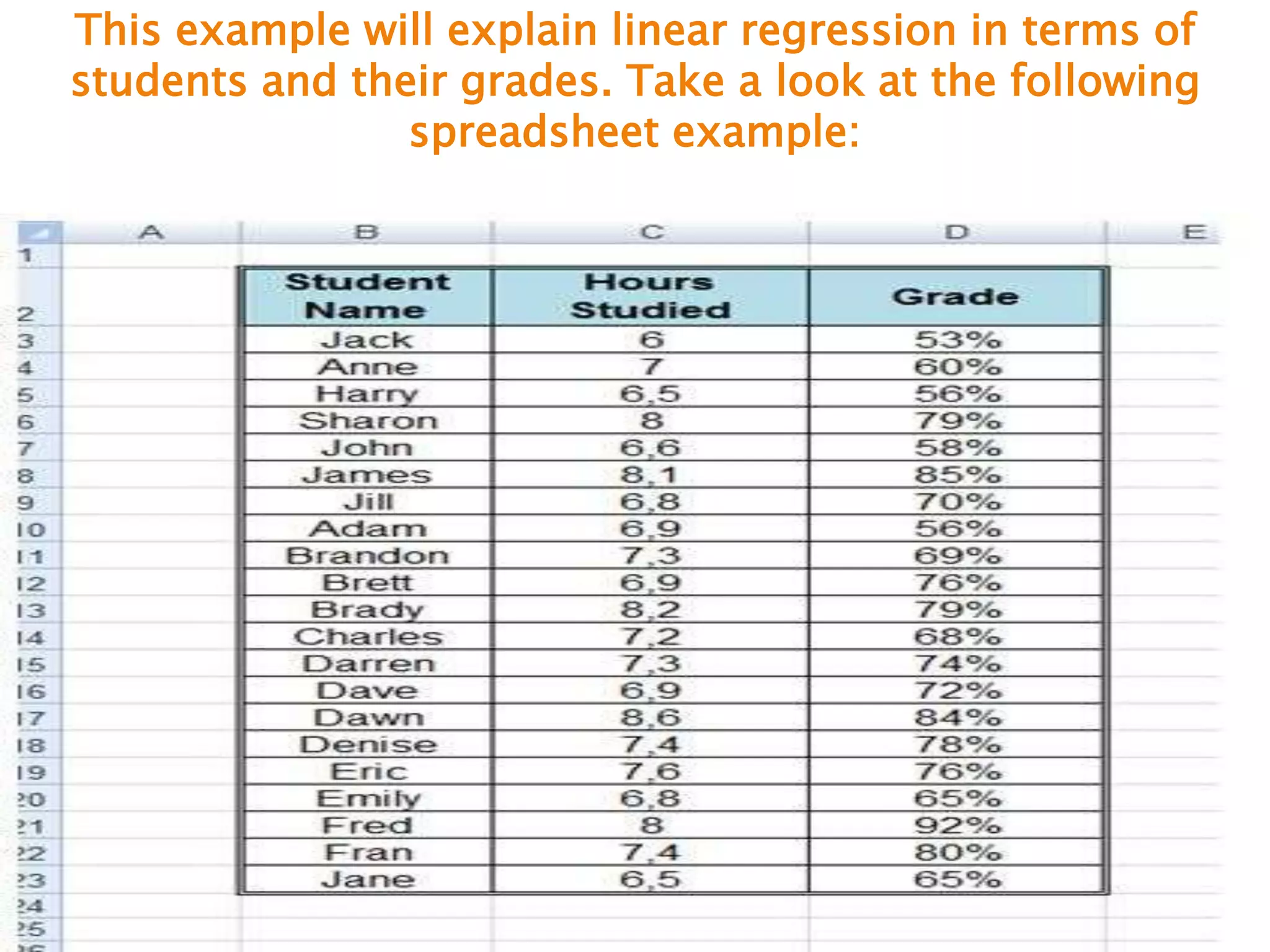
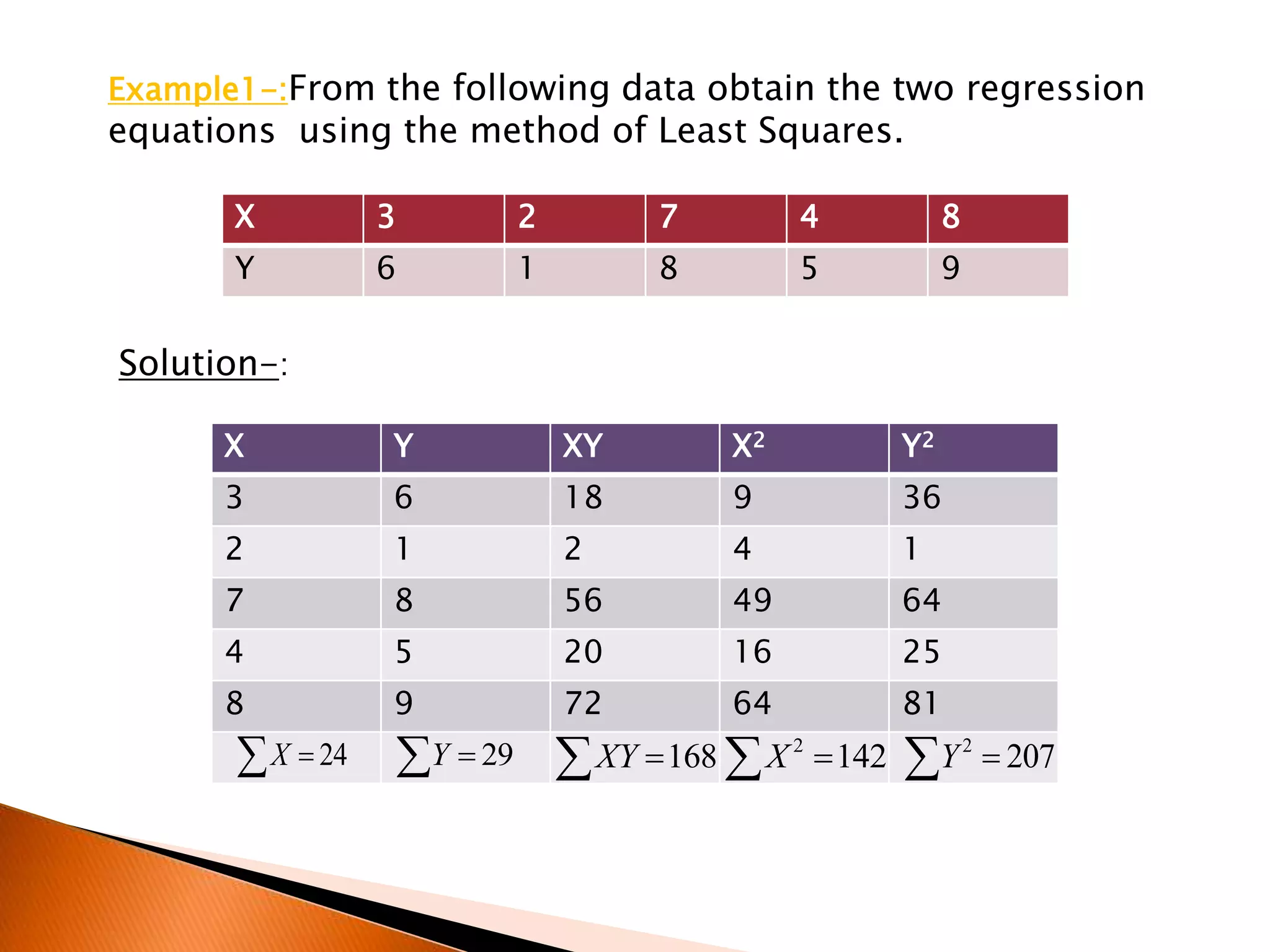
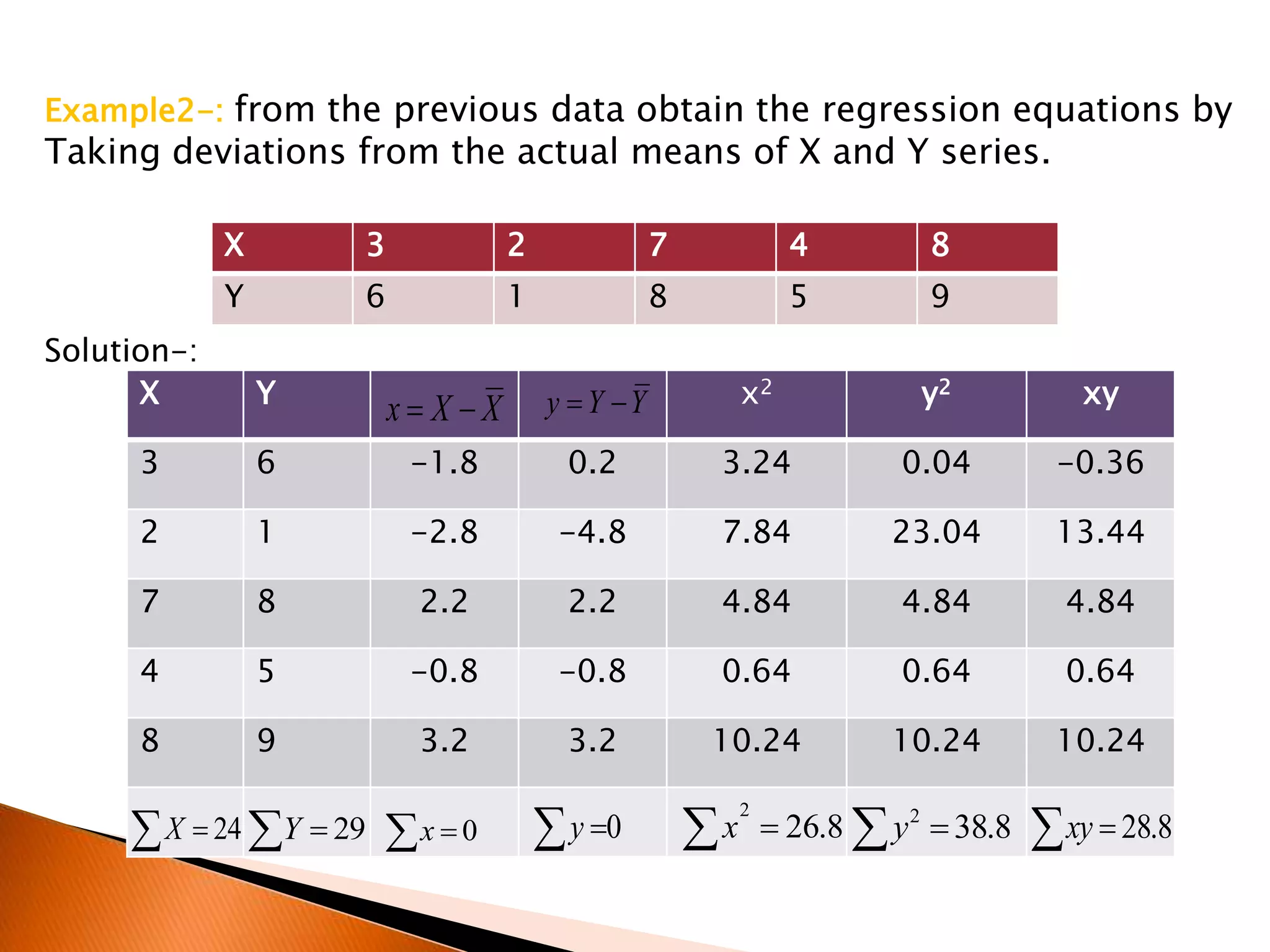
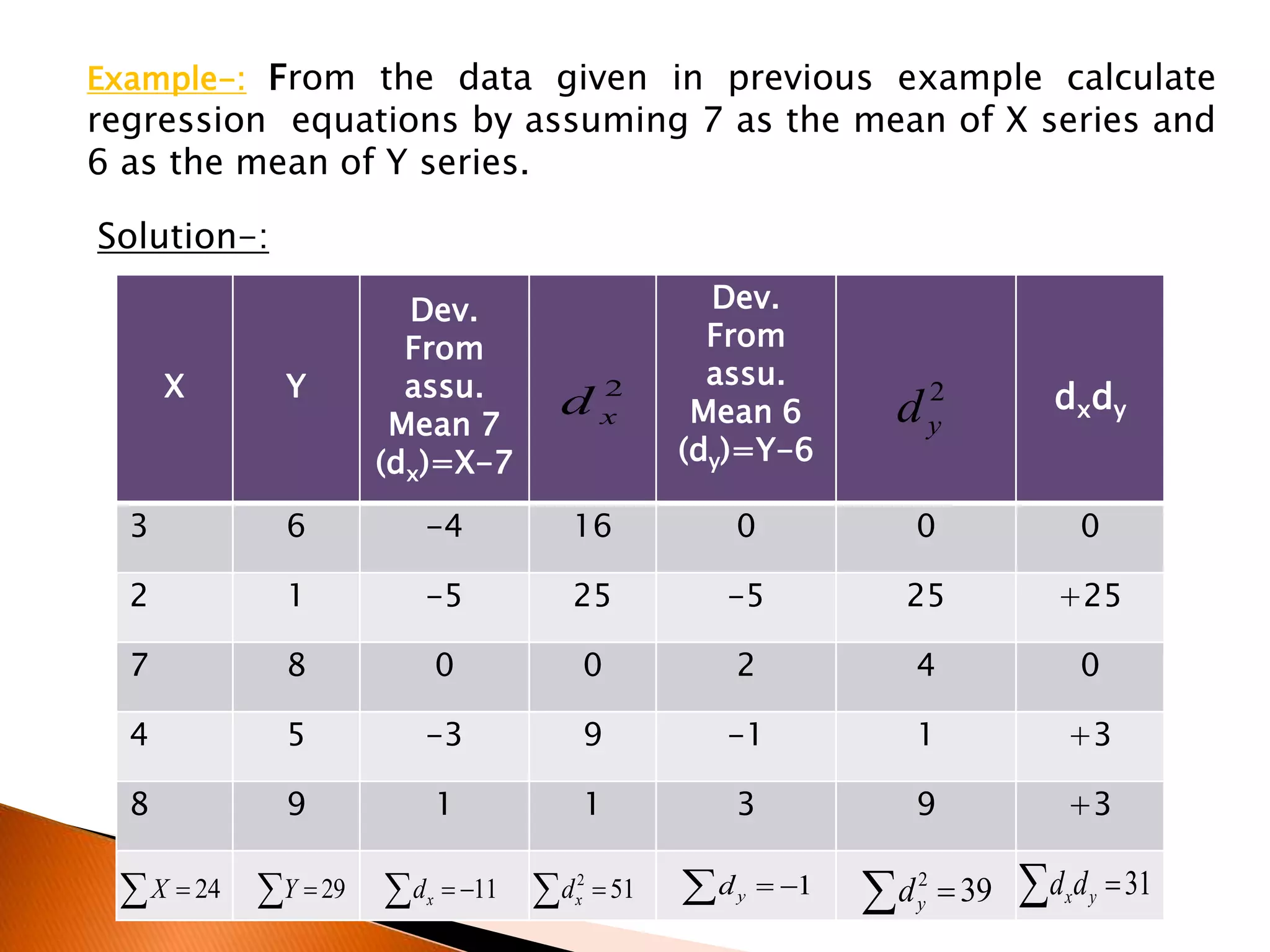
This document presents a presentation on regression analysis submitted to Dr. Adeel. It includes: - An introduction to regression analysis and its uses in measuring relationships between variables and making predictions. - Methods for studying regression including graphically, algebraically using least squares, and deviations from means. - An example calculating regression equations using data on students' grades and scores through least squares and deviations from means. - Conclusion that the regression equations match those obtained through other common methods.

2. PRESENTATION ON
REGRESSION ANALYSIS
submitted to:
Dr.Adeel

3. Group members:
 Muhammad Fazeel
 Zohaib Shafiq
 Jamal Ahmad
 Abdul Wahab
 Muhammad Adeel

4.  Regression is the measure of the average relationship
between two or more variables in terms of the
original units of the data. It is unquestionable the
most widely used statistical technique in social
sciences. It is also widely used in biological and
physical science.

5.  Regression analysis help us make prediction
outside of the given data. If we give
prediction with in the range the given data is
called interpolation.
 If we give prediction outside the range of
given data value it is called extrapolation.

7. The earliest form of regression was the method
of least squares, which was published
by Legendre in 1805, and by Gauss in 1809.
The term "regression" was used by British
biometrician sir Francis Galton in the (1822-1911),
to describe a biological phenomenon.
Sir Galton's work on inherited characteristics of
sweet peas led to the initial conception of linear
regression.

8. Importance of Regression Analysis
Regression analysis helps in three important ways :-
• It provides estimate of values of dependent
variables from values of independent variables.
• It can be extended to 2or more variables, which is
known as multiple regression.
• It shows the nature of relationship between two or
more variable.

9.  Regression analysis is the most useful as it
studies the variables individually and
determines their significance with greater
accuracy. Say, for example, you want to find
out the effect of protein shakes and exercise
on the weight of a person undergoing a
fitness program. Or you want to study the
relationship between salaries and
qualification on the job performance of an
employee.

10.  These studies will naturally involve a lot of
co-related variables that will individually have
an effect on the dependent variable. These
complex questions can be easily answered
with the help of regression analysis.

11.  . It’s used for many purposes like forecasting,
predicting and finding the causal effect of
one variable on another. For example, the
effects of price increase on the customer’s
demand or an increase in salary causing a
change in spending etc.
 If you are a statistician or analyst, a student
or professional, you will find regression
analysis is an important tool for modelling
and analyzing data.

12. USES IN ORGANIZATION
In the field of business regression is widely used.
Businessman are interested in predicting future
production, consumption, investment, prices,
profits, sales etc. So the success of a
businessman depends on the correctness of the
various estimates that he is required to make. It
is also use in sociological study and economic
planning to find the projections of population,
birth rates. death rates etc.

13. This example will explain linear regression in terms of
students and their grades. Take a look at the following
spreadsheet example:

14. METHODS OF STUDYING REGRESSION:
REGRESSION
GRAPHICALLY
FREE HAND CURVE
LESAST SQUARES
ALGEBRAICALLY
LESAST SQUARES
DEVIATION METHOD FROM
AIRTHMETIC MEAN
DEVIATION METHOD FORM
ASSUMED MEAN
Or

15. The linear equation is specified as follows:
Y = a + bX
Where Y = dependent variable
X = independent variable
a = constant (value of Y when X = 0)
b = is the slope of the regression line

16.  a can be positive or negative. In high school
algebra, you may have referred to a as the
intercept. This is because a is the point at which the
slope line passes through the Y
axis.
 b (the slope coefficient) can be positive or
negative. A positive coefficient denotes a positive
relationship and a negative coefficient denotes a
negative relationship.

17. Algebraically method-:
1.Least Square Method-:
The regression equation of X on Y is :
X= a+bY
Where,
X=Dependent variable
Y=Independent variable
The regression equation of Y on X is:
Y = a+bX
Where,
Y=Dependent variable
X=Independent variable
And the values of a and b in the above equations are found
by the method of least of Squares-reference . The values of a
and b are found with the help of normal equations given
below:
(I ) (II )
 
 


2
XbXaXY
XbnaY
 
 


2
YbYaXY
YbnaX

18. Example1-:From the following data obtain the two regression
equations using the method of Least Squares.
X 3 2 7 4 8
Y 6 1 8 5 9
Solution-:
X Y XY X2 Y2
3 6 18 9 36
2 1 2 4 1
7 8 56 49 64
4 5 20 16 25
8 9 72 64 81
  24X   29Y  168XY 1422
X 2072
Y

19.   XbnaY
   2
XbXaXY
Substitution the values from the table we get
29=5a+24b…………………(i)
168=24a+142b
84=12a+71b………………..(ii)
Multiplying equation (i ) by 12 and (ii) by 5
348=60a+288b………………(iii)
420=60a+355b………………(iv)
By solving equation(iii)and (iv) we get
a=0.66 and b=1.07

20. By putting the value of a and b in the Regression equation Y on X
we get
Y=0.66+1.07X
Now to find the regression equation of X on Y ,
The two normal equation are
 
 


2
YbYaXY
YbnaX
Substituting the values in the equations we get
24=5a+29b………………………(i)
168=29a+207b…………………..(ii)
Multiplying equation (i)by 29 and in (ii) by 5 we get
a=0.49 and b=0.74

21. Substituting the values of a and b in the Regression equation X and Y
X=0.49+0.74Y
2.Deaviation from the Arithmetic mean method:
The calculation by the least squares method are quit cumbersome when the
values of X and Y are large. So the work can be simplified by using this
method.
The formula for the calculation of Regression Equations by this method:
Regression Equation of X on Y- )()( YYbXX xy 
Regression Equation of Y on X-
)()( XXbYY yx 

 2
y
xy
bxy

 2
x
xy
byx
and
Where, xyb
yxband = Regression Coefficient

22. Example2-: from the previous data obtain the regression equations by
Taking deviations from the actual means of X and Y series.
X 3 2 7 4 8
Y 6 1 8 5 9
X Y x2 y2 xy
3 6 -1.8 0.2 3.24 0.04 -0.36
2 1 -2.8 -4.8 7.84 23.04 13.44
7 8 2.2 2.2 4.84 4.84 4.84
4 5 -0.8 -0.8 0.64 0.64 0.64
8 9 3.2 3.2 10.24 10.24 10.24
XXx  YYy 
  24X   29Y 8.26
2
x 8.28xy8.382
y  0x 0 y
Solution-:

23. Regression Equation of X on Y is
 
 
49.074.0
8.574.08.4
8.5
8.38
8.28
8.4
2






YX
YX
YX
y
xy
bxy
Regression Equation of Y on X is
)()( XXbYY yx 
 
66.007.1
)8.4(07.18.5
8.4
8.26
8.28
8.5
2






XY
XY
XY
x
xy
byx
………….(I)
………….(II)
)()( YYbXX xy 

24. It would be observed that these regression equations are
same as those obtained by the direct method .
3.Deviation from Assumed mean method-:
When actual mean of X and Y variables are in fractions ,the
calculations can be simplified by taking the deviations from
the assumed mean.
The Regression Equation of X on Y-:
  
  


 22
yy
yxyx
xy
ddN
ddddN
b
The Regression Equation of Y on X-:
  
  


 22
xx
yxyx
yx
ddN
ddddN
b
)()( YYbXX xy 
)()( XXbYY yx 
But , here the values of and will be calculated by
following formula:
xyb yxb

25. Example-: From the data given in previous example calculate
regression equations by assuming 7 as the mean of X series and
6 as the mean of Y series.
X Y
Dev.
From
assu.
Mean 7
(dx)=X-7
Dev.
From
assu.
Mean 6
(dy)=Y-6
dxdy
3 6 -4 16 0 0 0
2 1 -5 25 -5 25 +25
7 8 0 0 2 4 0
4 5 -3 9 -1 1 +3
8 9 1 1 3 9 +3
Solution-:
2
xd 2
yd
  24X   29Y   11xd   1yd 512
xd  392
yd  31yxdd

26. The Regression Coefficient of X on Y-:
  
  


 22
yy
yxyx
xy
ddN
ddddN
b
74.0
194
144
1195
11155
)1()39(5
)1)(11()31(5
2








xy
xy
xy
xy
b
b
b
b
8.5
5
29

 Y
N
Y
Y
The Regression equation of X on Y-:
49.074.0
)8.5(74.0)8.4(
)()(



YX
YX
YYbXX xy
8.4
5
24

 X
N
X
X

27. The Regression coefficient of Y on X-:
  
  


 22
xx
yxyx
yx
ddN
ddddN
b
07.1
134
144
121255
11155
)11()51(5
)1)(11()31(5
2








yx
yx
yx
yx
b
b
b
b
The Regression Equation of Y on X-:
)()( XXbYY yx 
66.007.1
)8.4(07.1)8.5(


XY
XY

28. Conclusion:
 It would be observed the these regression
equations are same as those obtained by the least
squares method and deviation from arithmetic
mean .