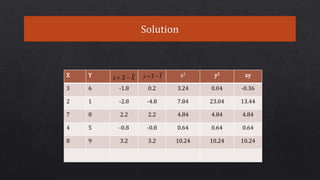
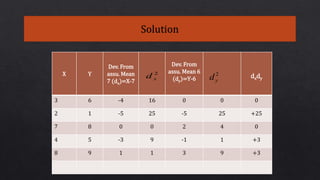
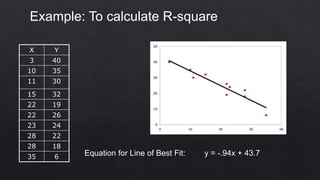
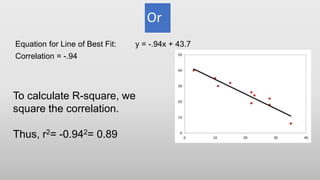
This document defines and explains various types of regression analysis including linear, logistic, polynomial, stepwise, ridge and lasso regression. It discusses the key differences between correlation and regression. It also covers topics such as the least squares method, R-squared/coefficient of determination, adjusted R-squared, limitations of regression analysis and applications of regression analysis.

1. By
Shivangi Sarabhai, Simran Sakshi
& Sonam Kharwar
BBM
DEI

2. Contents

3. INTRODUCTION
o The dictionary meaning of the term “Regression” is the act of
returning or going back.
o The term regression was first used by sir “Francis Galton” in
1877 while studying the relationship between the height of
fathers and sons.
o This term introduced by him in the paper “Regression towards
mediocrity in hereditary stature”.

4. o “Regression is the measure of the average relationship
between two or more variables in terms of the original units of
the data.”
- Blair
“The term regression analysis refers to the methods by which
estimates are made of the variables from a knowledge of the
values of one or more other variables and to the measurement
of the errors involved in the estimation.”
- Morris Hamburg
Definition of Regression

5. Difference between Correlation and
Regression
S. NO.
Correlation Regression
1. Correlation coefficient is a
measure of degree of co-
variability or association
between X and Y.
The objective of regression
analyses is to the study of
nature of relationship
between the variables so
that we may be able to
predict the values of one on
the basis of another.

6. S. NO Correlation Regression
2. It is merely a tool of ascertaining
the degree of relationship
between two variable and,
therefore, we cannot say that
one variable is the cause and
the other is effect. The variables
may be affected by some
unknown common factor.
In regression analysis one variable is
taken as dependent while the other as
independent-thus making it possible to
study the cause and effect relationship.
3. Correlation coefficient is
independent of change of scale
and origin.
Regression coefficient is independent
of change of origin but not of scale.

7. S.
NO
Correlation Regression
4. In this 𝑟𝑥𝑦 is a measure of direction
and degree of linear relationship
between two variable X and Y. 𝑟𝑦𝑥
and 𝑟𝑥𝑦 are symmetric, it is
immaterial which of X and Y is
dependent variable and which is
independent variable.
In regression analyses the regression
coefficients 𝑏 𝑥𝑦 and 𝑏 𝑦𝑥 are not
symmetric, and hence it definitely
makes a difference as to which
variable is dependent and which is
independent.

8. Types of Regression
Linear Regression Logical Regression
Polynomial
Regression
Stepwise
Regression
Ridge Regression Lasso Regression

9. Linear Regression

10. Logistic Regression

11. Polynomial regression

12. Y= b0 + b1x + Ԑ
E(Y) = b0 + b1x
Ŷ = b0 + b1x
SIMPLE LINEAR REGRESSION MODEL
SIMPLE LINEAR REGRESSION EQUATION
ESTIMATED SIMPLE LINEAR REGRESSION EQUATION

13. REGRESSION
GRAPHICALLY FREE HAND CURVE
LEAST SQUARES
ALGEBRAICALLY
LEAST SQUARES
DEVIATION
METHOD FROM
ARITHMETIC
MEAN
DEVIATION
METHOD FROM
ASSUMED MEAN

14. Least Square Method
 A procedure for using sample data to find the estimated regression equation.
 It uses the sample data method to provide the values of b0 and b1 that minimize
the sum of the squares of the deviations between the observed values of the
dependent variable Y and the estimated values of the dependent variable Ŷ.
 The criterion for the least squares method is given as: min ∑(Yi – Ŷi)2
 The error on either side of the regression line has to be minimized.

15.  
 


2
YbYaXY
YbnaX
 
 


2
XbXaXY
XbnaY

17. X Y XY X2 Y2
3 6 18 9 36
2 1 2 4 1
7 8 56 49 64
4 5 20 16 25
8 9 72 64 81

18.  
 


2
YbYaXY
YbnaX

19.  
 


2
XbXaXY
XbnaY
X=0.49+0.74Y

21. )()( YYbXX xy 
)()( XXbYY yx 

 2
y
xy
bxy

 2
x
xy
byx
xyb yxb

23. X Y x2 y2 xy
3 6 -1.8 0.2 3.24 0.04 -0.36
2 1 -2.8 -4.8 7.84 23.04 13.44
7 8 2.2 2.2 4.84 4.84 4.84
4 5 -0.8 -0.8 0.64 0.64 0.64
8 9 3.2 3.2 10.24 10.24 10.24
XXx  YYy 

24. )()( YYbXX xy 
 
 
49.074.0
8.574.08.4
8.5
8.38
8.28
8.4
2






YX
YX
YX
y
xy
bxy

25. )()( XXbYY yx 
 
66.007.1
)8.4(07.18.5
8.4
8.26
8.28
8.5
2






XY
XY
XY
x
xy
byx

27. )()( YYbXX xy 
)()( XXbYY yx 
xyb yxb
  
  


 22
yy
yxyx
xy
ddN
ddddN
b
  
  


 22
xx
yxyx
yx
ddN
ddddN
b

29. X Y
Dev. From
assu. Mean
7 (dx)=X-7
Dev. From
assu. Mean 6
(dy)=Y-6 dxdy
3 6 -4 16 0 0 0
2 1 -5 25 -5 25 +25
7 8 0 0 2 4 0
4 5 -3 9 -1 1 +3
8 9 1 1 3 9 +3
2
xd 2
yd

30.   
  


 22
yy
yxyx
xy
ddN
ddddN
b
74.0
194
144
1195
11155
)1()39(5
)1)(11()31(5
2








xy
xy
xy
xy
b
b
b
b

31. 49.074.0
)8.5(74.0)8.4(
)()(



YX
YX
YYbXX xy

32.   
  


 22
xx
yxyx
yx
ddN
ddddN
b
07.1
134
144
121255
11155
)11()51(5
)1)(11()31(5
2








yx
yx
yx
yx
b
b
b
b

33. )()( XXbYY yx 
66.007.1
)8.4(07.1)8.5(


XY
XY

34. R-square or Coefficient of determination
R squared or coefficient of determination indicates the proportionate amount of
variation in the responsible variable y explained by the independent variables x in
the linear regression model.
It provides a good measure of how well the estimated regression equation fits the
data.
The larger the R-squared is, the more variability is explained by the linear regression
model.
The closer r2 is +1, the better the line fits the data.
r2 will always be a positive number.
R2 = 1 indicates that the regression line perfectly fits the data.

35. X Y
3 40
10 35
11 30
15 32
22 19
22 26
23 24
28 22
28 18
35 6 Equation for Line of Best Fit: y = -.94x + 43.7
Example: To calculate R-square

36. X Y
Predicted Y
Value
Error
(predicted
value-y)
Error
Squared
Distance
between Y values
and their mean
Mean
distances
squared
3 40 40.88 .88 .77 14.8 219.04
10 35 34.30 -.70 .49 9.8 96.04
11 30 33.36 3.36 11.29 4.8 23.04
15 32 29.60 -2.40 5.76 6.8 46.24
22 19 23.02 4.02 16.16 -6.2 38.44
22 26 23.02 -2.98 8.88 .8 .64
23 24 22.08 -1.92 3.69 -1.2 1.44
28 22 17.38 -4.62 21.34 -3.2 10.24
28 18 17.38 -.62 .38 -7.2 51.84
35 6 10.80 4.8 23.04 -19.2 368.65
Mean: 25.2 Sum: 91.81 Sum: 855.60
Equation for Line of Best Fit: y = -.94x + 43.7

37. 1-
Sum of squared distances between the
actual and predicted Y values
Sum of squared distances between the
actual Y values and their mean
1-
91.81
855.60
= 1- 0.11
= 0.89
R2 =

38. Or
Correlation = -.94
To calculate R-square, we
square the correlation.
Thus, r2= -0.942= 0.89
Equation for Line of Best Fit: y = -.94x + 43.7

39.  Adjusted R-square is a modification of R-square that adjusts
for the number of terms in a model.
 R-square always increases when a new term is added to a
model, but adjusted R-square increases only if the new term
improves the model more than would be expected by chance.
 This makes Adjusted R-square more useful for comparing
models with a different number of predictors.
 R-squared increases if we increase the number of
variables in the regression model.
R squared, a property of the fitted model, is a structure with two fields:
•Ordinary — Ordinary (unadjusted) R-squared
•Adjusted — R-squared adjusted for the number of coefficients

40. Uses of Regression Analysis
Helps in establishing a functional relationship between two or more
variables
As most of the problems of economic analysis is based on cause and
effect relationships, regression analysis is a highly valuable tool in
economics and business research
It predicts the values of dependent variables from the values of
independent variables
We can calculate the coefficient of correlation and coefficient of
determination with the help of regression coefficients

41. APPLICATIONS
 Regression.xlsx

42. o In making estimates from a regression equation, it
is important to remember that the assumption is
being made that relationship has not changed since
the regression equation was computed.
Another point worth remembering is that
relationship shown by the scatter diagram, may not
be the same if the equation is extended beyond the
values used in computing the equation.
Limitations of Regression

43. o for example
there may be a close linear relationship between
the yield of a crop and the amount of fertilizer
applied, with the yield increasing as the amount
of fertilizer is increased. It would not be logical,
however, to extend this equation beyond the
limits of experiment for it is quite likely that if the
amount of fertilizer were increase indefinitely, the
yield would eventually decline as too much
fertilizer was applied.

44. References
 http://www.hedgefund-index.com/d_rsquared.asp
 http://www.ats.ucla.edu/stat/stata/faq/mi_r_squared.htm
 http://in.mathworks.com/help/stats/coefficient-of-determination-r-squared.html?requestedDomain=www.mathworks.com
 http://www.graphpad.com/guides/prism/6/curve-fitting/index.htm?r2_ameasureofgoodness_of_fitoflinearregression.htm
 http://blog.minitab.com/blog/statistics-and-quality-data-analysis/r-squared-sometimes-a-square-is-just-a-square
 http://blog.minitab.com/blog/adventures-in-statistics/regression-analysis-tutorial-and-examples