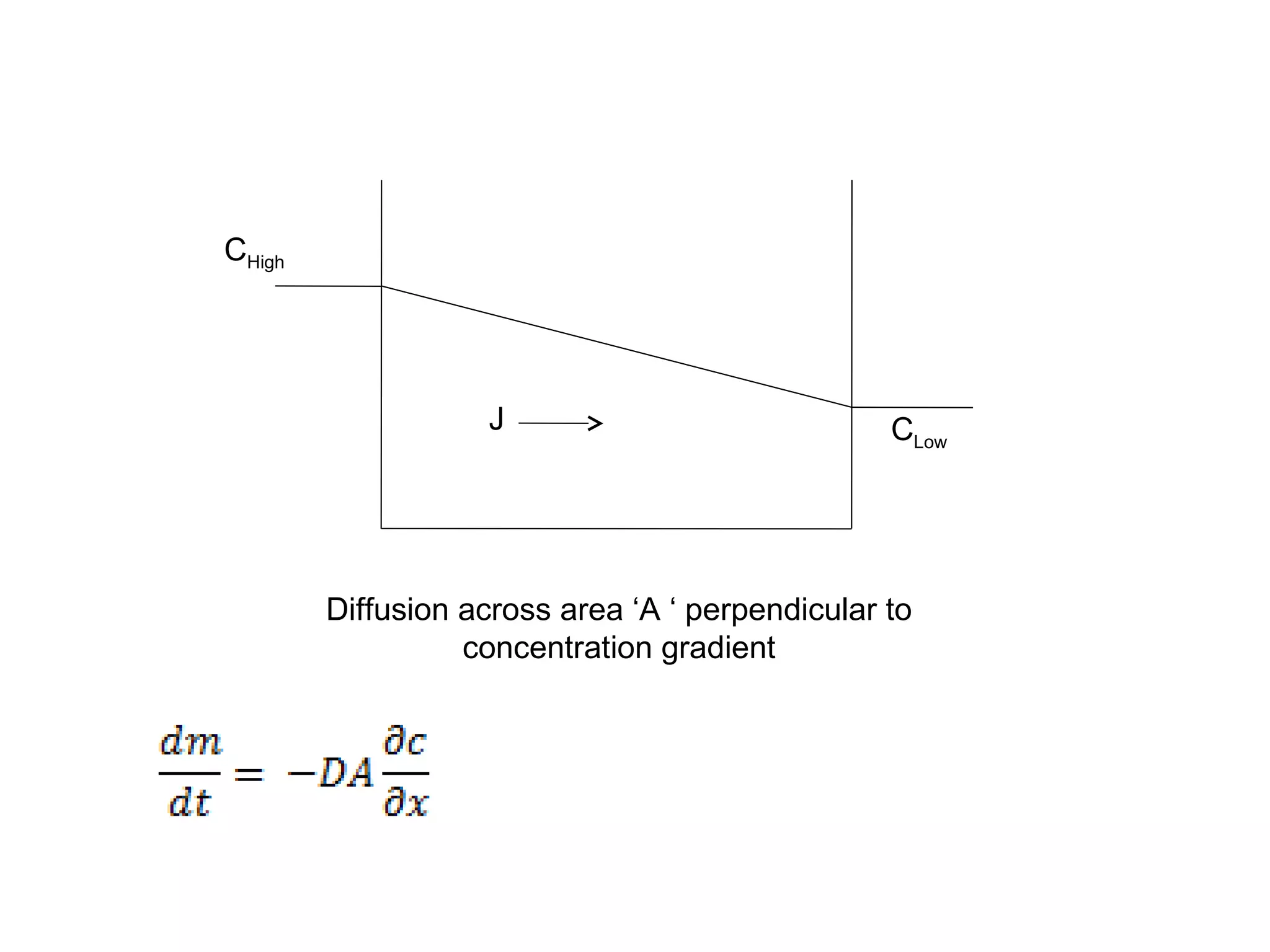
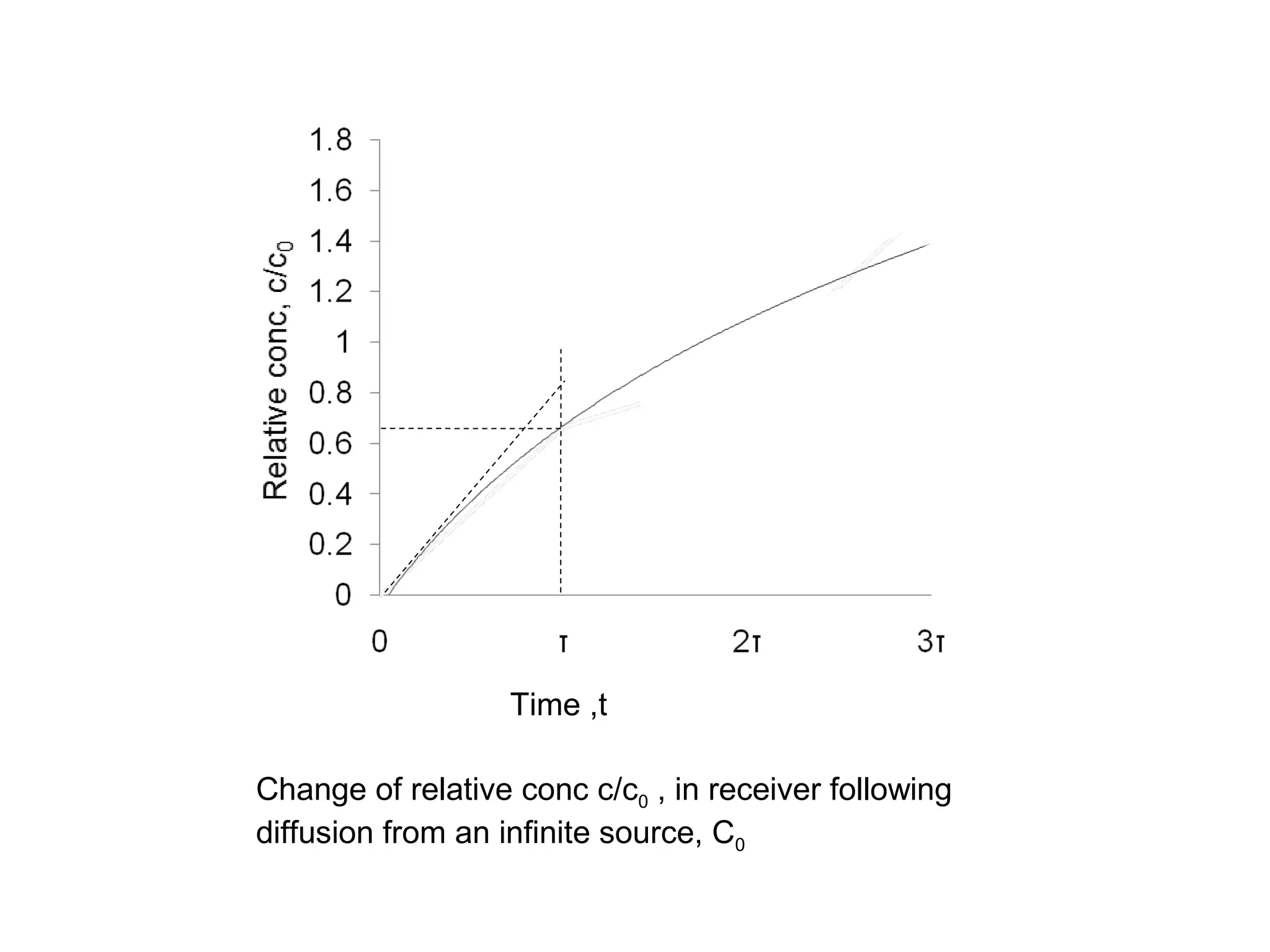
This document discusses the absorption of moisture by different fibers. It explains that the rate of moisture absorption depends on factors like temperature, humidity, thickness, and fiber type. The absorption process involves the slow diffusion of water molecules through the fiber over time until equilibrium is reached. This diffusion is modeled using Fick's laws of diffusion. Fick's first law states that the rate of diffusion is proportional to the concentration gradient, while Fick's second law accounts for how concentration changes over time as moisture penetrates the fiber. The document provides examples of using these laws to analyze moisture absorption in fibers and other materials.

1. VIVEK YADAV,,,,,,,TC NITRA
TECHNICAL CAMPUS
• A PRESENAION ON MOISTURE
ABSORPTION OF DIFFERENT FIBRE

2. Rate Of Absorption Of Moisture
• Textile materials take a long time to come
into equilibrium with their surrounding e.g
Drying after Washing.
• Rate depends on temperature, air
humidity, wind velocity, surroundings,
thickness of material, density of material,
nature of fibre etc.

3. • Slowness of Conditioning – May be a
technical nuisance, because textiles
have to be conditioned before
processing or sale.
• Advantageous – Valuable stabilizing
influence : absorbent fibrous materials
in a room will prevent rapid changes in
humidity or temperature.
• Study – Factors that play a part in
change of conditions in textiles.

4. DIFFUSION OF MOISTURE
• Slow Conditioning – Slowness with which
water molecules diffuse through the fibre
or through the air to the fibre.
• If concentration of H2O molecules ( or of
any other substance with which one is
concerned ) varies from place to place in a
given medium ( e.g – air or fibre
substance ), the molecules will diffuse
from regions of high concentration to
regions of low concentration until their
distribution becomes uniform.

5. Fick’s Equation – (First Law)
• Rate of transport of diffusing substance passing
through a cross-section ‘A’ is proportional to the
concentration gradient of moisture.
• Units – cm square/sec.
• D = Diffusion coefficient
• D ~ cm 2/sec
• Determined experimentally and in tables.
A = Unit cross sectional area
J= Mass of moisture passing
throu’ unit cross section

6. CHigh
CLow
J
Diffusion across area ‘A ‘ perpendicular to
concentration gradient

7. Fick’s first law has limited use.
• Practical problem, which can be solved ---
Membrane problem
• Flux ‘J’ Mass of moisture passing through
a unit cross-section :
• Problem – A membrane separates two
flowing streams of gases that have
different concentration of an impurity.

8. • Steady State Flux of impurity through
membrane is
D = Diffusion coefficient of an impurity through the
membrane.
J = Flux of impurity through the membrane per
unit area of membrane

9. • Fick’s first law is useful here because
concentration gradient is constant & at
steady state ‘D’ is constant
Most Problems in Diffusion, i.e, Textile
fibres –
Region where ‘c’ changes with time
Fibre experiences an increase in moisture
content with absorption.
In such cases, we cannot use Fick’s first
law

10. J1 J2
Δx
J1
J2
X1 X2
Diffusion of Impurity through a bar

11. DIFFUSION OF AN IMPURITY THROUGH A
SOLID BAR
• Flux through this bar of unit cross-
sectional area at x coordinate 1.
Since J1 is not equal to J2, the concentration
of species ‘c’ in the volume changes with
time
Fick’s Second Law – Flux that
corresponds to experimental conditions

12. • Law of Mass Conservation,
Substituting the expression for J from Fick’s
First Law,
This is Fick’s Second Law.
Simpler form where D is a constant & not a function of x
or c.

13. • Problem – To determine about how long it
will take for a fibre to absorb or desorb
moisture.
• Complications arise in fibres where
diffusion coefficient may vary with time.
• ( Absorption – Molecules removed from
diffusion process )
cannot be solved unless some relation
between D & c can substituted.

14. Diffusion Into A Receiver From An
Infinite Source Of Concentration Co
On integrating & assuming as initial
conditions c = 0 at t = 0,
C0
C
c=0
at
t=0

15. Time ,t
Change of relative conc c/c0 , in receiver following
diffusion from an infinite source, C0

17. M = Mass needed to bring the adsorbent to
equilibrium.

18. where
• C1 = Initial concentration at surface of
adsorbent.
• Co = Concentration at surface of
conditioning solution.

19. • For a homogeneous cylinder of length ‘l’
& radius ‘r’ in which there is a change of
conditions at surface such as to cause a
change in the equilibrium concentration in
the cylinder from C2 to Co, the mass
observed is given by product of the
volume of the cylinder and change in
concentration.