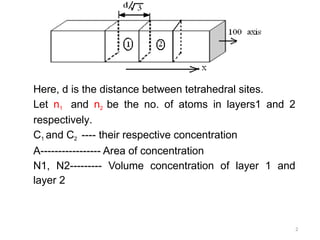
Fick's first law of diffusion describes the relationship between the rate of solute transfer and concentration gradient, stating that the flux density is proportional to the gradient, with diffusivity as a constant. The law has limitations, prompting the development of Fick's second law to account for measurable quantities and changes in flux density over time and distance. Fick's second law elaborates that the rate of change of volume concentration is proportional to the derivative of the concentration gradient.

1. Fick’s First Law of Diffusion
Based on analogy between material transfer in a solution and heat
transfer by conduction.
J=rate of transfer of solute per unit area or diffusion flux
N=concentration of solute (function of x and t only)
x=coordinate axis in the direction of solute flow
t=diffusion time
D=diffusivity (Diffusion constant)
Statement: The local rate of transfer of solute per unit area per unit time
is proportional to the concentration gradient of the solute and defines the
proportionality constant as diffusivity of the solute. The negative sign
shows the flow towards lower concentration of solute.
1

2. Here, d is the distance between tetrahedral sites.
Let n1 and n2 be the no. of atoms in layers1 and 2
respectively.
C1 and C2 ---- their respective concentration
A----------------- Area of concentration
N1, N2--------- Volume concentration of layer 1 and
layer 2
2

3. We assume atoms jump at a frequency of v such that,half of them
jump right and the other half jump left.
So, the net flow of atoms across plane R in direction of x is
=
Similarly,
net flow across the plane
= =
3

4. n1 =
& n2 =
=
Concentration gradient =
=
= )
=)
= ) =
4

5. Lets introduce j ---- flux density
flux -------------number of units passing through a boundary area
per unit time.
=
and d are constants
------------ D
----------------------Flicks first law of diffusion
Statement :
Flux density or rate of change of atoms per area is directly
proportional to the concentration gradient or change in volume
concentration () for a given displacement.
5

6. 6
Limitation of first law
• Though it describes diffusion process
accurately.
• But, has no convenient measure of current
density of the impurity.
• Thus, second law developed to describe the
concept with more readily measurable
quantities.

7. 7
Flick’s second law of diffusion
• Moving from P1 to P2 impurity concentration changes
and so does flux density from j1 to j2
• We know,
Let flux density entering at plane P1 = Aj
& Let flux density entering at plane P2 = A dj
Now, if the plates are separated by a distance dx, the rate of
accumulation of the particles in the region between the
planes =
The change in flux is equal to the accumulation of the
particles in the region between the plates,
= - A dj

8. 8
Flick’s second law of diffusion
= - A dj
=
But,
----------------------Flicks first law of diffusion
= ) = D
Statement:
The rate of change of volume concentration is directly
proportional to the derivate of concentration gradient