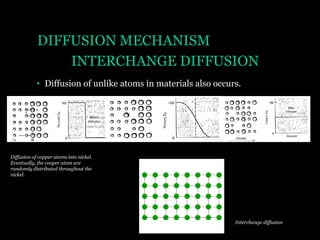
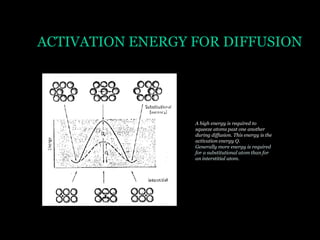
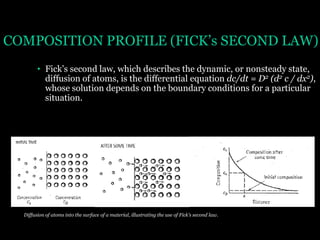
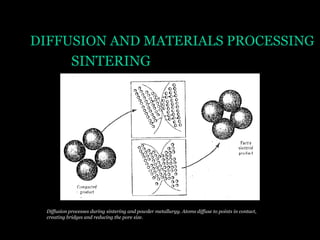
This document discusses the process of diffusion in materials. It defines diffusion as the movement of atoms within a material driven by concentration gradients. There are four main mechanisms of diffusion: self-diffusion, interchange diffusion, vacancy diffusion, and interstitial diffusion. Diffusion is thermally activated and follows the Arrhenius equation, requiring atoms to overcome an activation energy barrier. Fick's first law describes the flux of atoms down a concentration gradient, while Fick's second law models the change in concentration over time. Diffusion plays a key role in processes like grain growth, diffusion bonding, and sintering of materials.

1. DIFFUSION
Luis Linde Torres
Phase Transformation
12th of December, 2013

2. INDEX
1.
INTRODUCTION
2. STABILITY OF ATOMS
3. DIFFUSION MECHANISM
4. ACTIVATION ENERGY FOR DIFFUSION
5. RATE OF DIFFUSION (FICK’s FIRST LAW)
6. COMPOSITION PROFILE (FICK’s SECOND LAW)
7.
DIFFUSION AND MATERIAL PROCESSING

3. INTRODUCTION
• Diffusion is the movement of atoms within a material.
Atoms move in a predictable fashion to eliminate
concentration differences and produce homogeneous,
uniform composition. These movements are required for
many of the treatments that we perform on materials.
• Diffusion is required for the heat treatment of metals, the
manufacture of ceramics, the manufacture of transistor and
solar cells.
Interstitial Atomic diffusion across a 4-coordinated lattice.

4. STABILITY OF ATOMS
• We know that imperfections could be introduced into the
lattice of a crystal. These imperfections are not stable or at
rest. Atoms possess some thermal energy and they will
move. An atom may move from a normal lattice point to
occupy a nearby vacancy. An atom may move from one
interstitial site to another. Rate c _ 0
• The ability of atoms and imperfections to diffuse increases
as the temperature or thermal energy. The rate of movement
is related to temperature o thermal energy by the Arrhenius
equation:

5. STABILITY OF ATOMS
ARRHENIUS EQUATION
• C0 is a constant.
• R is the gas constant (8.314 J·mol-1·K-1).
• T is the absolute temperature (K).
• Q is the activation energy (J·mol-1) required to cause the
imperfection to move.

6. DIFFUSION MECHANISM
• The are four important mechanisms by which atoms diffuse:
 Self Diffusion
Interchange Diffusion
 Vacancy Diffusion
 Interstitial Diffusion

7. DIFFUSION MECHANISM
SELF-DIFFUSION
(SUBSTITUTIONAL)
• Even in absolutely pure solid materials, atoms move from
one lattice position to another. This process, know as selfdiffusion can be detected by using radioactive tracers.
Although self-diffusion occurs continually in all materials,
the effect on the material’s behaviour is not significant.

8. DIFFUSION MECHANISM
INTERCHANGE DIFFUSION
• Diffusion of unlike atoms in materials also occurs.
Diffusion of copper atoms into nickel.
Eventually, the cooper atom are
randomly distributed throughout the
nickel.
Interchange diffusion

9. DIFFUSION MECHANISM
VACANCY DIFFUSION
• In self-diffusion, an atom leaves its lattice sit to fill a nearby
vacancy. As diffusion continues, we have a counter-current
flow of atoms and vacancies, called vacancy diffusion.
• The number of vacancies, which increases as the
temperature increases, helps determine the extent of both
self-diffusion and diffusion of substitutional atoms.
Vacancy diffusion animation.

10. DIFFUSION MECHANISM
INTERSTITIAL DIFFUSION
• When an small interstitial atom is present in the crystal
structure, the atom moves from one interstitial site to
another. No vacancies is required for this mechanism. Partly
because there are many more interstitial sites than
vacancies.
• Interstitial diffusion is expected to be rapid.
Interstitial diffusion animation.

11. ACTIVATION ENERGY FOR DIFFUSION
• A diffusing atom must squeeze past the surrounding atomos
to reach its new site. In order for this to happen, energy
must be supplied to force the atom to its new position. The
atom is originally in a low-energy, relatively stable location.
• In order to move to a new location, the atom must overcome
an energy barrier. The energy barrier is the activation
energy Q. heat supplies the atom with the energy needed to
exceed this barrier.

12. ACTIVATION ENERGY FOR DIFFUSION
A high energy is required to
squeeze atoms past one another
during diffusion. This energy is the
activation energy Q.
Generally more energy is required
for a substitutional atom than for
an interstitial atom.

13. RATE OF DIFFUSION (FICK’s FIRS LAW)
• The rate at which atoms diffuse in a material can be
measured by the flux J, which is defined as the number of
atoms passing through a plane of unit area per unit time.
• Fick’s firs law explains the net flux of atoms:

14. RATE OF DIFFUSION (FICK’s FIRS LAW)
• J is the flux (atoms·m-2·s-1).
• D is the diffusity or diffusion coefficient (m2·s-1).
•
is the concentration gradient (atoms/m-3·m)
• Several factors affect the atoms during diffusion.
Illustration of the
concentration gradient

15. RATE OF DIFFUSION (FICK’s FIRS LAW)
CONCENTRATION GRADIENT
• The concentration gradient shows how the composition of
the material varies with distance.  is the difference
c
concentration over the distance  The concentration
x.
gradient may be created when two materials of different
composition are placed in contact when a gas or liquid is in
contact with a solid material, when nonequilibrium
structures are produced in a material due.
The flux during diffusion is defined as
the number of atoms passing through
a plane of unit area per unit time.

16. COMPOSITION PROFILE (FICK’s SECOND LAW)
• Fick’s second law, which describes the dynamic, or nonsteady state,
diffusion of atoms, is the differential equation dc/dt = D2 (d2 c / dx2),
whose solution depends on the boundary conditions for a particular
situation.
Diffusion of atoms into the surface of a material, illustrating the use of Fick’s second law.

17. COMPOSITION PROFILE (FICK’s SECOND LAW)
• Fick’s second law, which describes the dynamic, or nonsteady state,
diffusion of atoms, is the differential equation dc/dt = D2 (d2 c / dx2),
whose solution depends on the boundary conditions for a particular
situation.
• One solution is:
• Cs is a constant concentration of the diffusing atoms at the surface of
the material.
• C0 is the initial uniform concentration if the diffusing atoms in the
material.
• Cx is the concentration of the diffusing atom at location x below the
surface after time t.

18. COMPOSITION PROFILE (FICK’s SECOND LAW)
• Fick’s second law, which describes the dynamic, or nonsteady state,
diffusion of atoms, is the differential equation dc/dt = D2 (d2 c / dx2),
whose solution depends on the boundary conditions for a particular
situation.
• One solution is:
• erf is error function and it is tabuled.

19. DIFFUSION AND MATERIALS PROCESSING
• Diffusional processes become very important when
materials are used or processed at elevated temperatures.
• We are going to consider three cases in which diffusion is
important.:
 Grain Growth
Diffusion Bonding
 Sintering

20. DIFFUSION AND MATERIALS PROCESSING
GRAING GROWTH
• A material composed of many grains contains a large
number of grain boundaries, which represent a high-energy
area because of the inefficient packing of the atomos.
• Grain growth involves the movement of grain boundaries,
permitting some grains to grow at the expense of other.
Diffusion of atoms across the grain boundary is required
and, consequently, the growth of the grains is related to the
activation energy needed for an atom to jump across the
boundary.
• High temperatures or low activation energies increase the
size of the grains.
• Many heat treatment can cause an excessive grain growth.

21. DIFFUSION AND MATERIALS PROCESSING
GRAING GROWTH
Grain growth occurs as atom diffuse across the grain boundary from one
grain to another
Grain growth variation

22. DIFFUSION AND MATERIALS PROCESSING
DIFFUSION BONDING
• Diffusion bonding, a method used to join materials, occurs
in three steps.
1.
The first step forces the two surfaces together at a high
temperature and pressure, flattening the surface, fragment
impurities and producing a high atom-to-atom area.
2.
Atoms diffuse along grain boundaries to the remaining voids.
The atoms condense and reduce the size of any voids in the
interface. This step occurs very quickly.
3.
The final step -final elimination of the voids- volume
diffusion, which is comparatively slow, must occur.

23. DIFFUSION AND MATERIALS PROCESSING
DIFFUSION BONDING
Diffusion bonding steps. The last image (d) represents the final result.

24. DIFFUSION AND MATERIALS PROCESSING
SINTERING
• A number of materials are manufactured into useful shapes
by a process that requires consolidation of small particles
into a solid mass. Sintering is the high-temperature
treatment that causes particles to join together and
gradually reduces the volume of pore space between them.
• Sintering is a frequent step in the manufacture of ceramic
components, as well as in the production of metallic parts
by powder metallurgy.
• A variety of composite materials are produced using the
same techniques.

25. DIFFUSION AND MATERIALS PROCESSING
SINTERING
Diffusion processes during sintering and powder metallurgy. Atoms diffuse to points in contact,
creating bridges and reducing the pore size.

26. BIBLIOGRAPHY
• The Science and Engineering of Materials
Askeland, Donald R., Third Edition.
• The Science and Engineering of Materials
Askeland, Donald R., Fourth Edition.
• Principles of Materials Science and Engineering
Smith, William F., Third Edition.
• Principles of Materials Science and Engineering
Smith, William F., Fourth Edition.
• Ciencia e Ingeniería de los Materiales
Sánchez Solís, Arturo.

27. BIBLIOGRAPHY
• www.wikipedia.org (some languages)
• www.slideshare.net
• www.ujaen.es