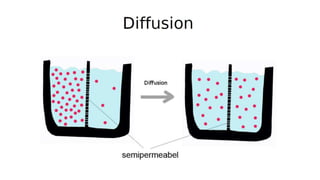
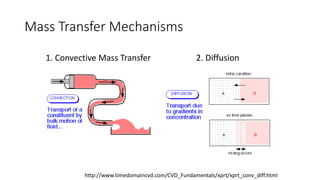
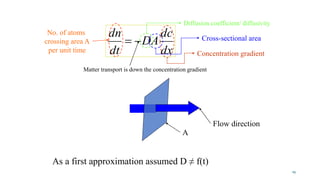
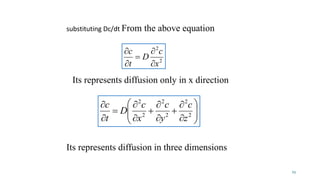
Mass transfer is the movement of mass from one location to another, such as between phases or components. It occurs through various processes like absorption, evaporation, drying, and distillation. Mass transfer involves both diffusive and convective transport mechanisms. Diffusion is the movement of molecules from a region of higher concentration to lower concentration down a concentration gradient via random molecular motion. Convection involves the bulk flow of a fluid carrying dissolved or suspended materials. Fick's first law describes the rate of diffusion, while Fick's second law describes how concentration changes over time at a given point for diffusion.

1. Mass transfer

2. • Mass transfer is the net movement of mass from one location, usually
meaning stream, phase, fraction or component, to another.
• Mass transfer occurs in many processes, such as absorption,
evaporation, drying, precipitation, membrane filtration, and
distillation.
• Mass transfer is used by different scientific disciplines for different
processes and mechanisms.
• The phrase is commonly used in engineering for physical processes
that involve diffusive and convective transport of chemical species
within physical systems.

3. DIFFUSION
• It is defined as a process of mass transfer of individual
molecules of a substance brought about by random
molecular motion and associated with a driving force
such as a concentration gradient.
3

4. 4

6. Mass Transfer Mechanisms
1. Convective Mass Transfer 2. Diffusion
http://www.timedomaincvd.com/CVD_Fundamentals/xprt/xprt_conv_diff.html

7. Convective transport
• Convective transport occurs when a constituent of the fluid (mass,
energy, a component in a mixture) is carried along with the fluid.
• Convection is mass transfer due to the bulk motion of a fluid. For
example, the flow of liquid water transports molecules or ions that
are dissolved in the water. Similarly, the flow of air transports
molecules present in air, including both concentrated species (e.g.,
oxygen and nitrogen) and dilute species (e.g., carbon dioxide)

8. Mass Transfer Mechanisms
3. Convective and Diffusion
http://www.timedomaincvd.com/CVD_Fundamentals/xprt/xprt_conv_diff.html

16. A system is said to be steady state , if the condition do
not vary with time
dc/dt or dm/dt
should be constant for diffusion
 To described steady state diffusion fick’s I and II laws
should be described
 Fick’s first law gives flux in a steady state of flow. Thus it
gives the rate of diffusion across unit cross section in the
steady state of flow.
 Second law refers to the change in concentration of diffusant
with time ‘t’ at any distance ‘x’.
STEADY STATE DIFFUSION
16

18. FICK´S I LAW
The amount “M” of material flowing through a unit
cross section “S” of a barrier in unit time “t” is known as the
flux “J”
18
dtS
dM
J
.

dx
dc
DJ 
The flux, in turn, is proportional to the concentration
gradient, dc/dx:

19. dx
dc
DA
dt
dn

No. of atoms
crossing area A
per unit time
Cross-sectional area
Concentration gradient
Matter transport is down the concentration gradient
Diffusion coefficient/ diffusivity
A
Flow direction
As a first approximation assumed D ≠ f(t)
19

20. Applications
•Release of drugs from dosage forms diffusion controlled
like sustained and controlled release products.
•Molecular weight of polymers can be estimated from
diffusion process.
•The transport of drugs from gastrointestinal tract, skin
can be predicted from principal of diffusion.
20

21. •Processes such as dialysis, micro filtration, ultra filtration,
hemodialysis, osmosis use the principal of diffusion.
•Diffusion of drugs into tissues and excretion through kidney can be
estimated through diffusion studies.
21

22. FICKS SECOND LAW
An equation for mass transport that emphasizes the
change in concentration with time at a definite location
rather than the mass diffusing across a unit area of barrier in
unit time is known as Fick’s second law
x
J
t
c





2
2
x
c
D
x
J






22
Differentiating the first law expression with respect to
x one obtains

23. Its represents diffusion only in x direction
substituting Dc/dt From the above equation
2
2
x
c
D
t
c






















2
2
2
2
2
2
z
c
y
c
x
c
D
t
c
23
Its represents diffusion in three dimensions

24. STEADY STATE
The solution in the receptor compartment is constantly
removed and replaced with fresh solvent to keep the
concentration at low level . This is know as “ SINK
CONDITION ” . The left compartment is source and right
compartment is sink.
The diffusant concentration In the left compartment
falls and rises in the right compartment until equilibrium is
attained , based on the rate of removal of diffusant from the
sink and nature of barrier .
24

25. When the system has been in existence a sufficient time,
the concentration of diffusant in the solution at the left and
right compartments becomes constant , but obviously not
same .
Then within each compartment the rate of change of
concentration dc/dt will be zero and by second law.
Concentration will not be constant but rather is likely to
vary slightly with time, and then dc/dt is not exactly zero.
The conditions are referred to as a “QUASI STATIONARY
STATE” and little error is introduced by assuming steady
state under these conditions.
02
2

dx
cd
D
dt
dc
25

26. Diffusion through membranes
Steady Diffusion Across a Thin Film and Diffusional
Resistance
26
• steady Diffusion across a thin film of thickness “h”,
•the concentration of both sides cd&cr kept constant,
•Diffusion occurs in the direction the higher concentration(Cd) to lower
concentration(Cr) the concentration of both sides cd&cr kept constant,
• after sufficient time steady state is achieved and the concentrations are constant at all
points,
•At steady state (dc/dt=0), ficks second law becomes

27. 02
2



z
e
D
R
cc
J 21 

)( 21 cc
h
D
J 
The term h/D is called deffusional resistance “R” the flux equation can be
written as
Integrating above equation twice using the conditions that at z=0,c=Cd and at
z=h, C=Cr yields the fallowing equation
after sufficient time steady state is achieved and the concentrations are
constant at all points
at steady state (dc/dt=0), ficks second law becomes
27
Permeability

28. If a diaphragm separates the two compartments of a diffusion
cell, the first law of fick’s may be written as
Where,
S=cross sectional area
H=thickness
c1 ,c2= concentration on the left and right sides of the
membrane
(c1-c2)/h within the diaphragm must be assumed to be
constant for quasi-stationary state to exist.
The concentrations c1,c2 can be replaced by partition
coefficient multiplied by the concentration Cd on the donor
side or Cr on receiver side.





 

h
cc
D
Sdt
dM
J 21
28

29. If sink condition in the receptor compartment 0rC
h
ccDSK
dt
dM rd )( 

rd c
c
c
c
K 21

d
d
PSC
h
DSKc
dt
dM

tPSCM d
sec)/(cm
h
DK
P 
P=permeability coefficient
P is obtained from slope of a linear plot permeant (M) vs. t.
29